В математике существует понятие наибольшего значения функции на заданном отрезке. Это число обозначается как f x0 и имеет особое значение для анализа поведения функции. Наибольшее значение функции можно интерпретировать как «пик» на графике функции, когда она достигает своего максимума в определенной точке.
Чтобы понять, что число f x0 является наибольшим значением функции на отрезке a b, необходимо проанализировать значения функции во всех точках этого отрезка. Если значение f x0 оказывается больше всех остальных значений функции на этом отрезке, то оно считается наибольшим.
Определение
Число f(x0) называется наибольшим значением функции на отрезке [a, b], если оно больше или равно значению функции во всех остальных точках этого отрезка.
Число f x0

Если значение функции f(x0) является самым большим на отрезке [a, b], то оно является глобальным максимумом. Это означает, что в окрестности точки x0 нет других значений функции, которые были бы больше, чем f(x0).
Чтобы найти число f x0, необходимо проанализировать функцию на отрезке [a, b], вычислить все значения f(x) для каждой точки x на этом отрезке и найти наибольшее из них. Значение f(x0) будет являться наибольшим значением функции на данном отрезке.
Число f x0 имеет важное значение в оптимизации и задачах нахождения экстремумов функций. Оно помогает установить максимальное значение функции на заданном отрезке и определить точку, в которой это значение достигается. Это может быть полезно при поиске наилучшего решения или оптимального значения в задачах оптимизации.
| Термин | Определение |
|---|---|
| Число f x0 | Наибольшее значение функции на отрезке [a, b], достигаемое в точке x0 и удовлетворяющее неравенству f(x) ≤ f(x0) для любого x на данном отрезке. |
| Глобальный максимум | Значение функции, которое является наибольшим на отрезке [a, b] и не имеет других значений, превосходящих его в окрестности точки x0. |
Наибольшее значение функции
Для определения наибольшего значения функции на отрезке, необходимо проверить все значения функции на этом отрезке и найти максимальное значение среди них. Важно учитывать, что наибольшее значение функции может существовать только внутри отрезка [a, b], поэтому необходимо ограничить поиск в этом диапазоне.
Существует несколько способов найти наибольшее значение функции на отрезке:
- Графический метод: построить график функции и определить точку, где она достигает максимального значения. Этот метод подходит для простых функций, у которых можно наглядно представить график.
- Аналитический метод: найти производную функции и найти ее корни в заданном диапазоне. Это будут точки, в которых функция достигает экстремумов. Затем проверить значения функции в этих точках и найти наибольшее значение.
- Итерационный метод: выбрать начальное приближение x0 в диапазоне [a, b] и последовательно приближать его к точке с наибольшим значением функции. Этот метод основывается на итеративном улучшении точности результата.
Выбор метода зависит от конкретной функции и ее сложности. В любом случае, необходимо учитывать особенности функции, ее производную (если она существует) и заданный диапазон для нахождения наибольшего значения функции на отрезке [a, b].
Ограничение
Для функции, заданной на некотором интервале (a, b), ее ограничение на этом интервале может быть найдено путем вычисления значений функции в различных точках интервала и сравнения этих значений. В результате получается наибольшее значение функции (максимум) или наименьшее значение функции (минимум) на интервале.
Процесс поиска ограничения функции на интервале может включать в себя анализ производной функции и точек экстремумов. Если функция является непрерывной на интервале (a, b), то ее ограничение обязательно существует на этом интервале.
| Ограничение на отрезке | Ограничение на интервале |
|---|---|
| Определяет наибольшее и наименьшее значение функции на заданном отрезке | Определяет наибольшее и наименьшее значение функции на заданном интервале |
| Может быть точкой или значениями функции на концах отрезка | Может быть точкой или значениями функции на границах интервала |
Ограничение функции на отрезке или интервале является важным понятием в математическом анализе и находит применение в различных областях, таких как оптимизация, экономика, физика и др.
Отрезок a b
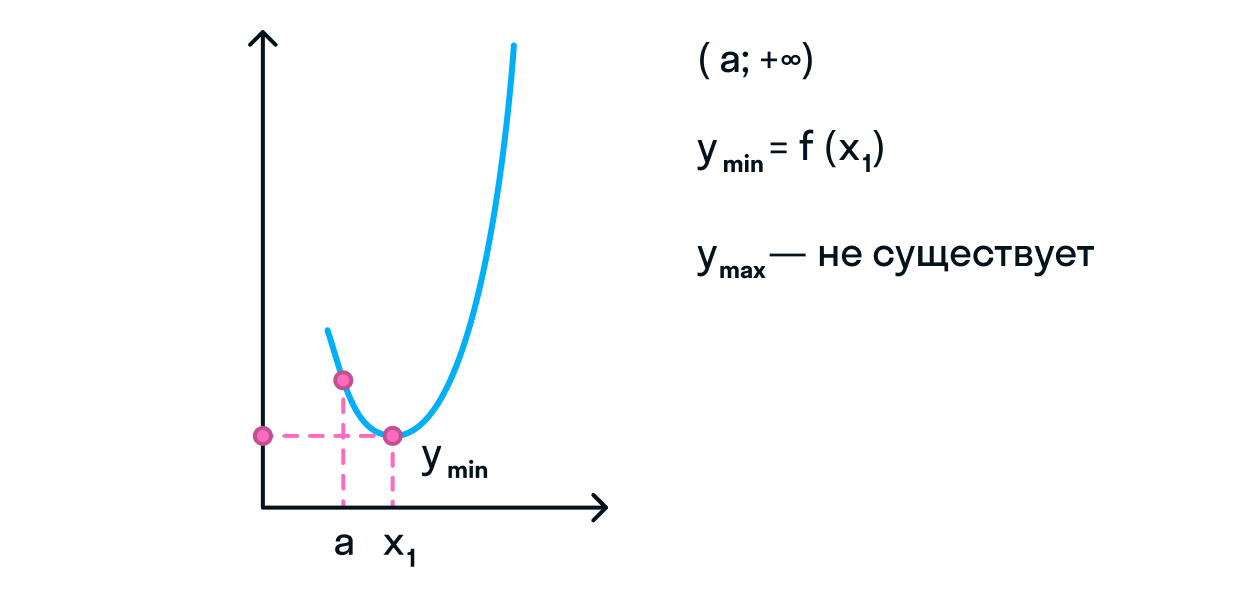
Для указания отрезка a b обычно используются квадратные скобки: [a, b]. Если одна или обе точки отрезка являются бесконечностью, то используются круглые скобки: (a, b) или (a, +∞) и т.д.
Отрезок a b может быть ограниченным или неограниченным. Ограниченный отрезок имеет конечные начальную и конечную точки, а неограниченный отрезок имеет хотя бы одну бесконечную точку. Например, отрезок [0, 1] является ограниченным, а отрезок (-∞, +∞) является неограниченным.