
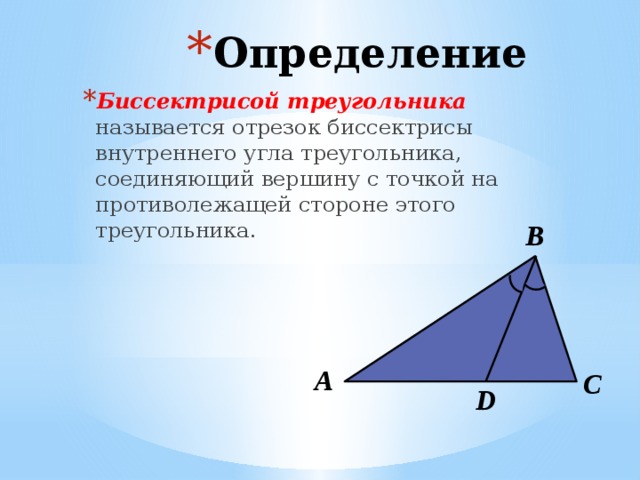
Биссектрисой треугольника называется отрезок, который делит внутренний угол треугольника на две равные по величине части. Она является прямой, исходящей из вершины треугольника и пересекающей противоположное ей сторону.
Биссектриса является одной из важных характеристик треугольника и играет важную роль в его свойствах. Она является осью симметрии треугольника, делящей его на две равные части. Биссектрисы всех трех углов треугольника пересекаются в одной точке, которая называется центром вписанной окружности.
Биссектриса треугольника также используется в различных задачах геометрии и расчетных задачах. Например, она помогает определить площадь треугольника по длине его биссектрисы и длинам сторон, а также использовать ее для нахождения углов треугольника при заданных условиях.
Что такое биссектриса треугольника?
В каждом треугольнике есть три биссектрисы, расположенные внутри фигуры. Они пересекаются в одной точке, называемой центром вписанной окружности. Центр вписанной окружности является центром симметрии треугольника и находится на пересечении биссектрис.
Биссектрисы треугольника играют важную роль в геометрии. Они помогают решать различные задачи, связанные с треугольниками, такие как нахождение высоты и площади треугольника, а также определение точек вписания окружностей и Incenter треугольника.
| Биссектриса треугольника | Свойства |
|---|---|
| Делит угол на два равных угла | Каждая биссектриса делит соответствующий угол на два равных угла. |
| Пересекаются в центре вписанной окружности | Три биссектрисы треугольника пересекаются в одной точке, являющейся центром вписанной окружности. |
| Могут быть использованы для нахождения площади треугольника | Биссектрисы могут помочь найти площадь треугольника с использованием формулы Герона. |
Использование биссектрис треугольника позволяет упрощать задачи и находить дополнительные свойства фигуры. Изучение биссектрис треугольника является важным этапом в изучении геометрии и может быть применено в различных областях, включая архитектуру, инженерное дело и физику.
Определение биссектрисы треугольника
Биссектрисы каждого угла треугольника пересекаются в одной точке, которая называется центром вписанной окружности треугольника. Центр вписанной окружности является центром равномерной симметрии треугольника, и относительно него все биссектрисы равны.
Биссектрисы треугольника имеют большое значение в геометрии, так как они связаны с различными свойствами треугольника. Например, биссектрисы являются основой для нахождения высот, медиан и центра тяжести треугольника. Также биссектрисы используются в решении задач с подобиями треугольников и нахождением отрезков, параллельных сторонам треугольника.
Свойства биссектрисы треугольника
Свойства биссектрисы треугольника:
- Биссектриса угла треугольника делит противолежащую сторону пропорционально отношению соседних сторон. То есть, отношение длины отрезка, на котором лежит биссектриса, к длине противолежащей стороны, равно отношению длин двух соседних сторон треугольника.
- Точка пересечения биссектрис треугольника лежит на окружности, описанной вокруг треугольника. Такая окружность называется окружностью биссектрис треугольника.
- Биссектриса угла треугольника является осью этого угла и делит противолежащую сторону на две равные части.
- В равнобедренном треугольнике биссектрисы всех углов являются медианами и высотами треугольника.
- В прямоугольном треугольнике биссектриса прямого угла является медианой и высотой треугольника, а также делит гипотенузу на отрезки с длинами, обратно пропорциональными ближнему и дальнему катетам треугольника.
Изучение свойств биссектрис треугольника позволяет лучше понять его геометрическую структуру и использовать их в решении различных задач.
Как найти биссектрису треугольника?
Биссектрисой треугольника называется отрезок, который делит один из углов треугольника на два равных угла. Она проходит через вершину этого угла и делящую его сторону.
Если известны длины сторон треугольника, можно найти биссектрису с помощью следующей формулы:
биссектриса = (2 * произведение корней длин двух смежных сторон) / (сумма длин этих двух смежных сторон)
Если известны углы треугольника, можно найти биссектрису с помощью следующей формулы:
биссектриса = (длина стороны треугольника * синус половины угла, делящегося биссектрисой) / (синус половины суммы остальных двух углов)
Для нахождения биссектрисы треугольника воспользуйтесь этими формулами и знаниями о сторонах и углах треугольника.
Формула для вычисления биссектрисы треугольника
Пусть дан треугольник ABC, а точка D – точка пересечения биссектрисы угла A с противоположной стороной BC. Длина биссектрисы AD может быть вычислена по формуле:
AD = 2 * sqrt(b * c * p * (p — a)) / (b + c)
где a, b и c – длины сторон треугольника, а p – полупериметр треугольника (p = (a + b + c) / 2).
Эта формула основана на теореме синусов и позволяет вычислить длину биссектрисы треугольника, используя только длины его сторон.
Примечание: при расчете биссектрисы треугольника необходимо учитывать порядок сторон. Например, в формуле биссектрисы AD сторона a соответствует углу A, а стороны b и c – сторонам BC и AC.
Примеры использования биссектрисы треугольника
Биссектрисы треугольника широко применяются в геометрии и строительстве. Вот несколько конкретных примеров использования биссектрисы треугольника:
1. В геометрических задачах, когда необходимо разделить угол на две равные части, можно использовать биссектрису треугольника. Это помогает найти точку, расположенную на биссектрисе, которая делит угол на две равные половины.
2. В треугольниках, где заданы длины сторон и требуется найти высоту, можно использовать биссектрису, чтобы разделить треугольник на два прямоугольных. Это позволяет использовать теорему Пифагора для нахождения высоты.
3. Внутри треугольника можно провести три биссектрисы, которые пересекаются в одной точке, называемой центром вписанной окружности. Это свойство полезно для нахождения центра вписанной окружности и решения задач, связанных с окружностями, вписанными в треугольники.
4. Биссектрисы также используются в архитектуре и инженерии при построении треугольных конструкций, таких как фермы или рамы. В таких случаях биссектрисы используются для определения углов и точек пересечения, что обеспечивает точность и прочность конструкции.
Таким образом, использование биссектрисы треугольника является важным инструментом в геометрии и строительстве, позволяющим решать разнообразные задачи и обеспечивать точность и прочность конструкций.
Роль биссектрисы в геометрии
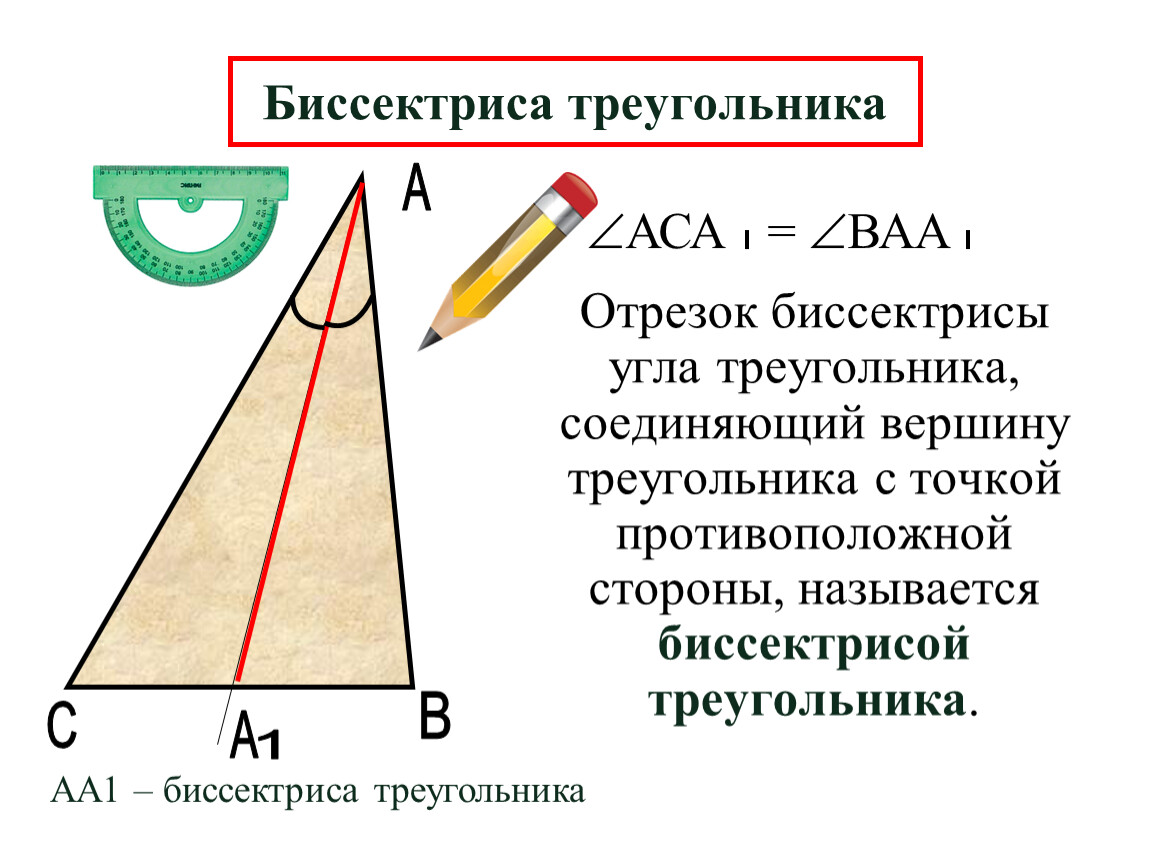
Биссектрисой треугольника называется отрезок, который делит внутренний угол треугольника на два равных угла. Биссектрисы служат важным инструментом в геометрии, используемым для решения различных задач и построений.
Одна из главных ролей биссектрисы – нахождение точки пересечения трёх биссектрис треугольника. Она называется центром вписанной окружности и является центральной точкой описанной окружности, вписанной в данный треугольник. Центр вписанной окружности имеет важное значение в геометрии, так как связан со многими другими характеристиками треугольника.
Ещё одним важным аспектом роли биссектрисы является нахождение биссектрисного треугольника. Биссектрисный треугольник получается путем соединения вершин треугольника с точками пересечения сторон с их соответствующими биссектрисами. Биссектрисный треугольник имеет несколько интересных характеристик, таких как равенство площадей.
Также биссектрисы используются для нахождения высоты треугольника. Для этого две биссектрисы и третья сторона образуют новый треугольник, в котором биссектрисы являются боковыми сторонами. Данная конструкция позволяет легко найти площадь и высоту треугольника.
Таким образом, биссектрисы треугольника играют важную роль в геометрии, помогая решать задачи, находить важные характеристики треугольника и проводить построения с использованием этих линий.
Полезные советы по работе с биссектрисой треугольника
- Используйте теорему угла-биссектрисы: для любого угла треугольника, биссектриса делит его на два угла, пропорциональные смежным сторонам треугольника.
- Зная длину биссектрисы треугольника и длины двух смежных сторон, можно найти длины оставшихся сторон треугольника с помощью теоремы Пифагора.
- Для нахождения длины биссектрисы треугольника можно использовать формулу: биссектриса — это отношение произведения длин двух смежных сторон к сумме длин этих сторон.
- Помните, что точка пересечения биссектрис треугольника образует центр вписанной окружности, которая касается всех сторон треугольника. Это свойство можно использовать для решения задач на построение треугольника по заданным условиям.
- Если требуется найти площадь треугольника с помощью биссектрисы, можно воспользоваться формулой Герона, где биссектриса будет одним из параметров.
Используя эти полезные советы, вы сможете более уверенно и эффективно работать с биссектрисой треугольника и решать различные задачи связанные с этой линией.
Вопрос-ответ:
Что такое биссектриса треугольника?
Биссектрисой треугольника называется отрезок, который делит угол треугольника пополам.
Зачем нужна биссектриса треугольника?
Биссектриса треугольника позволяет находить точку пересечения биссектрис разных углов треугольника, которая называется центр вписанной окружности. Это важно, так как вписанная окружность треугольника имеет много полезных свойств и используется в различных математических и геометрических задачах.
Как найти биссектрису треугольника?
Для нахождения биссектрисы треугольника нужно провести прямую, которая делит угол треугольника пополам. Это можно сделать с помощью линейки и циркуля.
Какие свойства имеет биссектриса треугольника?
Биссектриса треугольника имеет несколько важных свойств. Одно из них — биссектриса треугольника делит противоположную сторону треугольника на отрезки, пропорциональные длинам двух других сторон. Еще одно свойство — биссектриса треугольника составляет равные углы с двумя сторонами треугольника.
Где в жизни можно применить знание о биссектрисе треугольника?
Знание о биссектрисе треугольника может быть полезно в различных сферах жизни. Например, в архитектуре и строительстве для нахождения центра вписанной окружности треугольника, что может помочь в создании красивых и гармоничных форм. Также, это знание может быть полезно в геодезии и картографии для определения углов между направлениями.