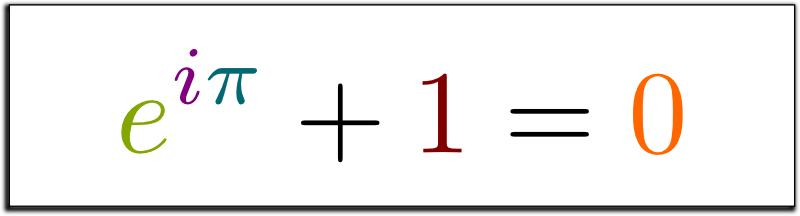
Число e – одно из самых уникальных и фундаментальных чисел в математике. Оно является основой для многих важных математических констант и само по себе обладает удивительными свойствами.
Число e неразрывно связано с понятием экспоненты и решением экспоненциальных уравнений. Точное значение e равно приблизительно 2,71828, однако оно является иррациональным числом и не может быть представлено десятичной дробью или конечным числом цифр.
Цифра e возникает, когда рассматривается предел приращения функции (1 + 1/n)^n при n, стремящемся к бесконечности. Эта функция интересна тем, что при увеличении значения n, мы получаем все более точное приближение к числу e. Оно также возникает как сумма бесконечного ряда 1/0! + 1/1! + 1/2! + 1/3! + …, которая сходится к числу e.
Число e широко используется в различных областях математики и физики. Оно является основой для вычислений процентных ставок, служит базой для логарифмов и экспоненциальных функций, а также находит применение в вероятностных расчетах и статистике. Благодаря своим свойствам, e позволяет описать многие явления природы и использовать их для решения сложных математических задач.
Число e в математике: его смысл и применение
Число e возникает при рассмотрении экспоненциальной функции, которая описывает рост или затухание некоторой величины со временем. В частности, формула для расчета значения функции при использовании числа e имеет вид:
f(x) = e^x
где x — любое действительное число.
Одно из основных применений числа e связано с вычислением сложных процентных ставок и непрерывного роста. Например, если вкладчик размещает сумму денег на счету с постоянной процентной ставкой, то формула для вычисления итогового баланса будет иметь вид:
| Период (лет) | Баланс (рубли) |
|---|---|
| 0 | 1000 |
| 1 | 1000 * e |
| 2 | 1000 * e^2 |
| 3 | 1000 * e^3 |
| n | 1000 * e^n |
Таким образом, число e позволяет учитывать непрерывный рост величины и является важным инструментом для финансовых расчетов.
Благодаря своим математическим свойствам, число e также неразрывно связано с другими основными константами, такими как пи (π), мнимая единица (i) и множество других математических функций и формул. Оно используется в различных областях науки и применяется при решении сложных задач в физике, экономике, статистике и других дисциплинах.
Таким образом, число e является одной из фундаментальных констант в математике и играет важнейшую роль при анализе и моделировании различных процессов с непрерывным ростом или изменением.
Что такое число e?
e было впервые определено Леонардом Эйлером в XVIII веке, и это число играет ключевую роль во многих областях математики и физики, таких как дифференциальное и интегральное исчисления, теория вероятностей, комплексный анализ и многих других.
Одна из самых известных формул, связывающая число e с другими математическими константами, называется формулой Эйлера, которая имеет вид:
| eiπ | = | -1 |
Также число e играет важную роль в ряде природных явлений, таких как рост популяции, устойчивость экономических систем и распределение случайных событий.
История и определение числа e
Число e определяется как предел последовательности (1 + 1/n)^n при n стремящемся к бесконечности. То есть, число e равно приближенно 2,718281828459045… Это иррациональное число, то есть, его десятичная запись не имеет периодичности и бесконечно продолжается без повторяющихся цифр.
Число e широко используется в различных областях науки и инженерии, особенно в математическом анализе, теории вероятностей, статистике и физике. Оно играет важную роль в ряде формул и уравнений, а также имеет решающее значение в таких областях, как дифференциальное и интегральное исчисление, комплексный анализ и эконометрика.
Число e можно назвать «натуральным экспонентом», так как оно связано с экспоненциальными функциями. Оно является основанием натурального логарифма, и обладает рядом свойств и особенностей, которые делают его незаменимым в математике и физике.
Математические свойства числа e
1. Определение числа e:
Число e определяется как предел суммы (1 + 1/n)^n при n, стремящемся к бесконечности. В результате получается приближенное значение числа e, которое составляет около 2.718281828459045.
2. Непрерывность и гладкость:
Число e является иррациональным, т.е. не может быть представлено в виде дроби. Оно также является трансцендентным числом, что означает, что нет алгебраического уравнения, корнем которого было бы число e. Число e непрерывно и гладко меняется с изменением аргумента.
3. Совместимость с логарифмическими функциями:
Число e имеет особое отношение к логарифмическим функциям. Его базисное свойство заключается в том, что производная функции ln(x) равна 1/x, а при x = e производная равна 1. Эта связь между числом e и логарифмическими функциями делает его полезным для решения различных задач и получения приближенных значений.
4. Связь с комплексными числами:
Число e также играет важную роль в комплексном анализе. Оно является главным числом в формуле Эйлера, которая устанавливает соотношение между экспоненциальной функцией и комплексными числами. Формула Эйлера имеет вид e^(iθ) = cos(θ) + i sin(θ), где i – мнимая единица, а θ – угол.
5. Применение в вероятностных распределениях:
В теории вероятностей число e является основой для экспоненциального распределения, показывающего, сколько времени проходит между последовательными событиями. При наличии постоянной интенсивности событий, распределение времени между событиями следует именно экспоненциальному закону с параметром e.
Таким образом, математические свойства числа e связаны с различными областями математики и науки. Оно является основой для множества математических моделей и имеет множество применений в решении задач различной сложности.
Применение числа e в математике
Одно из основных применений числа e – в теории вероятности и математической статистике. Оно является основанием для натурального логарифма и экспоненты, которые используются для моделирования различных случайных явлений. Например, при описании различных законов распределения, таких как нормальное, экспоненциальное или пуассоновское распределение.
Также число e используется в комплексном анализе, где часто возникают функции с экспоненциальным или тригонометрическими зависимостями, которые могут быть выражены с помощью числа e. Оно также играет важную роль в решении дифференциальных уравнений и матричных операциях, используемых в теории линейных дифференциальных уравнений.
Число e также связано с непрерывным процентным ростом и использованием приближенных методов вычисления непрерывного процента. В экономике оно применяется для вычисления накопленного эффекта процента, а в финансовой математике используется для оценки сложных процентных ставок.
Кроме того, число e имеет применение в теории информации и сжатии данных, где оно используется для описания энтропии и информационной емкости различных систем. Оно также находит применение в физике, биологии и других естественных науках для описания различных явлений.
| Область применения числа e | Примеры |
|---|---|
| Теория вероятности и статистика | Моделирование случайных явлений |
| Комплексный анализ | Решение дифференциальных уравнений |
| Финансовая математика | Вычисление накопленного эффекта процента |
| Теория информации | Описание энтропии и информационной емкости систем |
Формулы с использованием числа e
Некоторые из наиболее известных формул с использованием числа e:
| Формула | Описание |
| e = limn→∞ (1 + 1/n)n | Формула, определяющая число e как предел последовательности (1 + 1/n)n при n, стремящемся к бесконечности. |
| f(x) = ex | Формула, определяющая экспоненциальную функцию с основанием e. Значение функции f(x) равно e, возведенному в степень x. |
| ∫0∞ e-x dx = 1 | Формула определяет площадь под экспоненциальной кривой f(x) = e-x от 0 до бесконечности, которая равна 1. |
| eiπ + 1 = 0 | Формула Эйлера, которая объединяет числа e, π, и i (мнимую единицу) в уравнение, известное как идентитет Эйлера. |
Эти формулы и уравнения позволяют применять число e для решения различных задач и моделирования природных явлений в различных областях науки и техники, включая физику, экономику, и статистику.
Примеры практического применения числа e
-
Финансовые расчеты: Когда происходит накопление большой суммы денег на протяжении длительного периода времени, такой как инвестиции или банковский процент, число e играет важную роль. Оно связано сонижением процента начисления ипринципом сложных процентов.
-
Рост и децимация: При расчетах, связанных с экспоненциальным ростом или падением, число e обычно используется в формулах. Например, при моделировании популяции животных или росте бактерий.
-
Статистика и вероятность: Число e используется в статистических расчетах, таких как распределение Пуассона и экспоненциальное распределение. Оно также связано с формулой нормального распределения и является основой для вычисления вероятностей с помощью натурального логарифма.
-
Физические явления: Во многих физических явлениях, таких как электронные цепи, колебания и сосредоточенные силы, число e часто используется как основа для различных математических моделей и уравнений.
-
Математические исследования: Число e играет ключевую роль в различных областях математики, включая дифференциальное и интегральное исчисление, теорию вероятности и матричные вычисления.
Общепринятое математическое обозначение числа e послужило основой для разработки логарифмических, экспоненциальных и тригонометрических функций, которые являются фундаментальными для решения множества задач различных наук и отраслей.
Значение числа e в научных и ежедневных вычислениях
Значение числа e имеет огромное значение в математике и науке в целом. Оно часто встречается в различных математических формулах и уравнениях.
В математическом анализе число e является базовым параметром для построения натурального логарифма. Это связано с тем, что производная функции y = e^x равна самой функции, то есть ее график наклонен под углом 45 градусов к оси x. Это свойство делает число e незаменимым инструментом для вычисления экспоненциальных функций и служит основой для работы со сложными логарифмическими выражениями.
Число e также имеет практическое применение в ежедневных вычислениях. В финансовой математике оно играет важную роль при расчете сложных процентных ставок и приведении денежных потоков к единому времени. Вероятностные расчеты и статистика также используют число e для определения различных вероятностей и распределений.
В различных областях науки, таких как физика, химия и биология, число e и его экспоненциальная функция широко применяются для описания различных процессов и явлений. Например, они используются для моделирования роста популяций, распространения сигналов в электронике, кинетических процессов в химических реакциях и многих других.
Таким образом, число e является неотъемлемой частью математики и науки в целом. Его значение не только теоретическое, но и находит свое применение в решении практических задач в различных областях знания. Понимание его значения и свойств помогает углубить знания в математике и стать более опытным в научных и вычислительных исследованиях.
Вопрос-ответ:
Что такое число e в математике?
Число e — это особое математическое число, иррациональное число, которое приближенно равно 2,71828. Оно было введено в математику Леонардом Эйлером и является основанием натурального логарифма.
Какое значение имеет число e в математике?
Число e в математике имеет множество значений и применений. Оно является основой для комплексных, гиперболических и многих других видов функций. Также оно играет важную роль в решении дифференциальных уравнений и вероятностных распределений.
Зачем нужно число e в математике?
Число e является одним из самых важных чисел в математике. Оно позволяет решать различные задачи, связанные с экспоненциальными функциями, производными, интегралами, вероятностными распределениями и многими другими. Оно является фундаментальным элементом в различных отраслях математики и наук.
Как появилось число e в математике?
Число e было введено в математику Леонардом Эйлером. Он заметил, что есть некоторое число, которое при возведении в степень даёт само себя в качестве значения производной своих функций. Он обозначил это число как e и исследовал его свойства и применения.
Как использовать число e в математике?
Число e используется в математике для решения различных задач. Оно позволяет вычислять экспоненциальные функции, производные и интегралы. Также оно находит применение в финансовых расчетах, статистике, электронике и других областях, где требуется точное моделирование природных и социальных процессов.