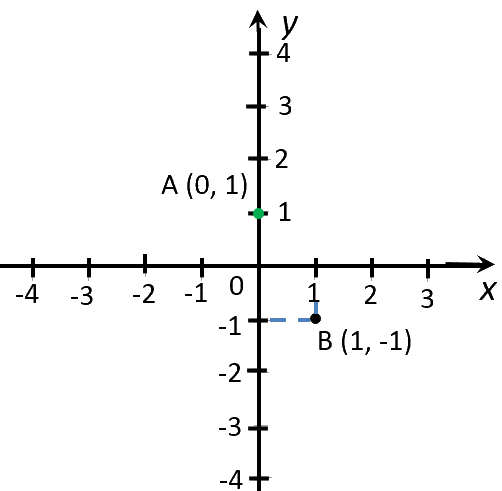
Функция является одним из основных понятий в математике. Она позволяет определить зависимость одной величины от другой, что является неотъемлемой частью анализа данных. В настоящей статье мы сфокусируемся на функции y k x.
Функция y k x представляет собой особый тип функции, где y — это зависимая переменная, x — независимая переменная, а k — параметр функции. В отличие от других функций, y k x может иметь неограниченное количество параметров, что делает ее весьма гибкой и многосторонней в использовании.
Название функции y k x выбирается на основе ее специфического предназначения. Именно оно отражает суть функции и позволяет быстро идентифицировать ее в математическом аппарате. Например, функция y k x может называться «логарифмическая», «экспоненциальная», «линейная» и т. д., в зависимости от ее математической формулы и свойств.
Какие функции называют функциями y k x?
Такие функции обычно записываются в виде y = f(x), где f(x) — это аналитическое выражение, зависящее от переменной x.
Функции y k x широко используются в математике и физике для описания различных явлений и процессов. Они позволяют устанавливать зависимость значения переменной y от значения переменной x при заданных условиях.
Примерами функций y k x могут быть линейные функции, квадратные функции, показательные функции, тригонометрические функции и др.
Одна из наиболее известных функций y k x — это прямая линия, которая описывается уравнением y = kx + b, где k — это угловой коэффициент, определяющий наклон прямой, а b — свободный член, определяющий смещение прямой по оси y.
Понятие y k x и его связь с графиком
Связь функции y k x с графиком изображается в виде прямой линии на координатной плоскости. Каждая точка на графике представляет собой пару значений (x, y), где x — значение аргумента, а y — значение функции.
Если k положительный, график функции будет проходить через начало координат и будет иметь положительный наклон вправо. Если k отрицательный, график будет иметь отрицательный наклон влево, а при k = 0 график будет параллель оси x.
График функции y k x позволяет визуализировать взаимосвязь между двумя переменными и анализировать их зависимость. Он может быть использован для прогнозирования значений функции при заданных значениях аргумента, а также для определения свойств функции, таких как монотонность и область значений.
Значение функций y k x в математике
Значение функции yk(x) может быть представлено графически в виде кривой на координатной плоскости, где ось x соответствует значению переменной x, а ось y — значению функции yk(x).
Примеры функций:
1. Линейная функция: yk(x) = kx. Здесь значение y линейно зависит от значения x.
2. Квадратичная функция: yk(x) = kx2. Здесь значение y квадратично зависит от значения x.
3. Тригонометрическая функция: yk(x) = ksin(x). Здесь значение y зависит от значения синуса угла x.
Важно отметить, что значение функции yk(x) может быть определено для любого значения x в домене функции, а параметр k может изменяться и влиять на форму графика функции.
Значение функций yk(x) играет важную роль в анализе, прогнозировании и моделировании различных явлений и процессов, а также в решении задач математической физики и естественных наук.
Примеры функций y k x в реальной жизни

1. Функция скорости движения тела
Представим себе автомобиль, который движется по прямой дороге. Функция y k x в данном случае может выразить зависимость скорости движения автомобиля от времени. Если x — время, прошедшее с начала движения, то y — скорость автомобиля в этот момент времени. Здесь k будет представлять собой коэффициент изменения скорости в зависимости от времени и других факторов.
2. Функция спроса на товар
При изучении экономики функция y k x может описывать зависимость спроса на товар от его цены. Если x — цена товара, то y — количество потребителей, желающих купить данный товар при этой цене. Здесь k будет определять эластичность спроса, то есть влияние изменения цены на количество потребителей.
Это только некоторые примеры применения функций y k x в реальной жизни. Эти функции помогают нам лучше понимать и предсказывать различные зависимости между величинами и находят применение в решении практических задач.
Интересные свойства функций y k x
Математическая функция y k x играет важную роль в различных областях науки и техники. Вот несколько интересных свойств, которые она обладает:
- Монотонность. Функция y k x может быть как монотонно возрастающей, так и монотонно убывающей в зависимости от значения параметра k и значения аргумента x. Это свойство делает функцию удобной для анализа тенденций и изменений в различных процессах.
- Ограниченность. В зависимости от выбора параметра k и аргумента x, функция y k x может быть ограниченной сверху или снизу. Это свойство часто используется для определения верхних и нижних границ в задачах оптимизации и определении экстремальных значений.
- Симметричность относительно оси. При определенных значениях параметра k и аргумента x функция y k x может обладать симметричностью относительно оси. Это свойство является основой для построения симметричных геометрических фигур и конструкций.
- Периодичность. Некоторые значения параметра k и аргумента x могут делать функцию y k x периодической. Такое свойство находит применение в анализе циклических процессов и расчетах, основанных на них.
Это лишь некоторые из интересных свойств функций y k x. В зависимости от контекста и области применения, эта функция может обладать еще множеством свойств, делающих ее полезной и значимой для решения различных задач.
Уравнения y k x и их решения
Решением линейного уравнения y = kx являются значения переменной x, для которых уравнение выполняется. То есть, для каждого значения x, найдется соответствующее значение y.
Если k равно нулю, то уравнение y = kx принимает вид y = 0, что означает, что прямая проходит через начало координат и параллельна оси OX.
Если k не равно нулю, то уравнение y = kx задает прямую, которая имеет наклон относительно оси OX. Знак числа k определяет направление наклона. Если k положительное, то прямая направлена вверх, если отрицательное — прямая направлена вниз.
Чтобы найти точку пересечения двух прямых, можно приравнять их уравнения и найти значение x, а затем подставить его в любое из уравнений, чтобы найти соответствующее значение y.
Примеры решения уравнений y = kx:
- Если k = 2 и x = 3, то y = 2 * 3 = 6
- Если k = -0.5 и x = 8, то y = -0.5 * 8 = -4
- Если k = 1.5 и x = -2, то y = 1.5 * -2 = -3
Роль функций y k x в научных исследованиях

В научных исследованиях функции yk(x) играют важную роль и используются для решения различных задач и построения моделей.
Функции yk(x) широко применяются в математике, физике, химии, экономике и других науках. Они являются математическими выражениями, которые устанавливают зависимость между переменными x и y в исследуемом явлении.
Использование функций yk(x) в анализе данных
Функции yk(x) применяются для анализа и обработки больших объемов данных. Они позволяют исследователям искать закономерности, осуществлять прогнозирование и построение математических моделей. Например, в экономических исследованиях функции yk(x) могут использоваться для прогнозирования показателей рынка и принятия решений о развитии бизнеса.
Примеры применения функций yk(x) в физических исследованиях
В физике функции yk(x) используются для описания и предсказания различных физических явлений. Например, в механике они могут быть использованы для моделирования движения тела, в электромагнетизме — для описания зависимости между электрическим полем и потенциалом.
Таким образом, функции yk(x) играют значительную роль в научных исследованиях, позволяя установить взаимосвязи между переменными, прогнозировать явления и строить математические модели для более глубокого понимания окружающего мира.
Вопрос-ответ:
Что такое функция y k x?
Функция y k x является математическим объектом, который связывает два множества чисел и сопоставляет каждому элементу одного множества элемент другого множества. Она может быть представлена в виде уравнения, графика или таблицы значений.
Какая роль функции y k x в математике?
Функция y k x играет важную роль в математике, поскольку она позволяет описывать и анализировать зависимость между переменными в различных областях знания. Она используется для моделирования явлений в физике, экономике, биологии и других науках.
Какие бывают виды функций y k x?
Существует множество видов функций y k x, каждый из которых имеет свои особенности. Некоторые из них включают линейные функции, квадратичные функции, показательные функции, логарифмические функции, тригонометрические функции и т. д. Каждый тип функции имеет свою формулу и свой график зависимости переменных.
Как можно представить функцию y k x в графическом виде?
Функцию y k x можно представить графически с помощью координатной плоскости, где ось x представляет значения переменной x, а ось y — значения функции y k x. График функции представляет собой точки, соответствующие парам значений x и y k x. Визуализация графика помогает понять характер зависимости и выделить особые точки и участки функции.