
В линейной алгебре матрица является одной из основных структурных единиц. Существует несколько видов матриц, каждый из которых имеет свои уникальные свойства и особенности. Одним из наиболее интересных типов является диагональная матрица, которая обладает рядом особенностей и применяется в различных областях.
Диагональная матрица представляет собой матрицу, у которой все элементы, кроме элементов, расположенных на главной диагонали, равны нулю. Главная диагональ — это линия, состоящая из элементов, расположенных от верхнего левого угла матрицы до нижнего правого. Это основное свойство, которое отличает диагональную матрицу от других типов.
Диагональные матрицы имеют ряд преимуществ и применяются в различных областях науки и техники. Одно из главных преимуществ — это экономия памяти и времени при выполнении операций, таких как умножение и сложение матриц. Это связано с тем, что в диагональной матрице большая часть элементов равна нулю, что позволяет существенно сократить вычислительные затраты.
Диагональные матрицы широко применяются в различных областях, таких как физика, экономика, статистика и многие другие. К примеру, в физике они используются для описания симметрии системы, в экономике — для моделирования и анализа финансовых показателей, а в статистике — для выполнения линейных регрессий и анализа данных.
Понятие диагональной матрицы
Для диагональной матрицы характерно следующее свойство: если элемент матрицы не принадлежит главной диагонали, то он равен нулю. Другими словами, если рассмотреть диагональную матрицу в виде двумерного массива a[i][j], то при i ≠ j элемент a[i][j] будет равен нулю.
Диагональные матрицы широко используются в математике и физике для решения различных задач. Они являются очень удобными для анализа и упрощения вычислений при работе с системами линейных уравнений или при преобразованиях координат в трехмерном пространстве.
Пример диагональной матрицы:
Пусть дана квадратная матрица A размером 3×3:
A = | 5 0 0 | | 0 3 0 | | 0 0 2 |
Матрица А является диагональной, так как все элементы вне главной диагонали равны нулю. В данном случае элементы на главной диагонали равны 5, 3 и 2.
Диагональные матрицы обладают рядом интересных свойств. Например, при умножении диагональной матрицы на вектор, каждый элемент вектора умножается на соответствующий элемент на главной диагонали матрицы, что позволяет упростить вычисления.
Также диагональные матрицы имеют некоторые важные характеристики, такие как определитель, собственные значения и собственные векторы.
Связь с единичной матрицей:
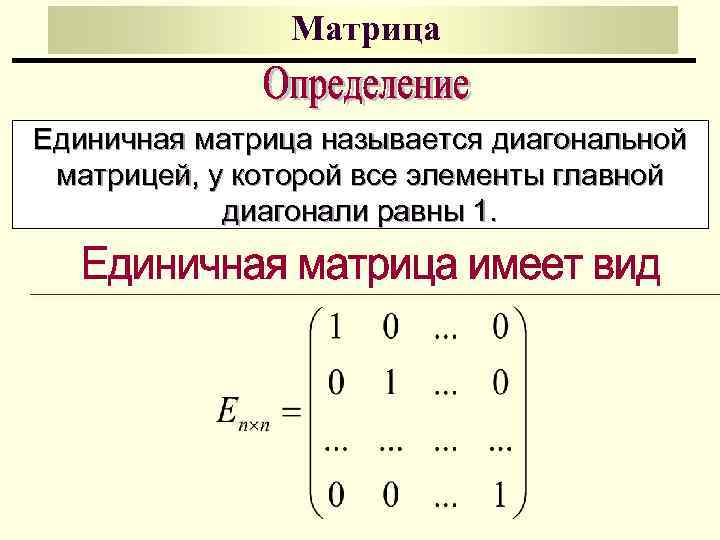
Единичная матрица — это частный случай диагональной матрицы, в котором все элементы на главной диагонали равны единице (1). Единичная матрица обозначается как I или E.
Другими словами, единичная матрица является диагональной матрицей, у которой на главной диагонали стоят единицы, а все остальные элементы равны нулю.
Например, единичная матрица размером 3×3 выглядит следующим образом:
I = | 1 0 0 | | 0 1 0 | | 0 0 1 |
Единичная матрица является нейтральным элементом относительно умножения матриц, что означает, что умножение любой матрицы на единичную матрицу не изменяет самой матрицы.
Также единичная матрица играет важную роль при нахождении обратной матрицы. Если квадратная матрица имеет обратную, то её обратная равна произведению обратной исходной матрицы на единичную матрицу.
Что такое диагональная матрица
В диагональной матрице нулевые элементы находятся вне главной диагонали и обычно отображаются в виде нулей. Ненулевые элементы, расположенные на главной диагонали, могут быть любыми числами.
Диагональная матрица имеет несколько интересных свойств. Например, умножение диагональной матрицы на вектор эквивалентно умножению каждого элемента вектора на соответствующий элемент на главной диагонали матрицы.
Важно отметить, что даже если все элементы вне главной диагонали равны нулю, матрица все равно считается диагональной, если хотя бы один элемент на главной диагонали не равен нулю.
Особенности диагональных матриц
Диагональные матрицы имеют несколько особенностей, которые делают их важными и полезными в различных областях науки и техники:
1. Простота
Одна из главных особенностей диагональных матриц — их простота. Так как большинство элементов матрицы равны нулю, операции с диагональными матрицами проще и быстрее выполнять, чем с обычными матрицами.
2. Свойства умножения
Умножение диагональной матрицы на другую матрицу имеет несколько свойств:
- Умножение на диагональную матрицу — при умножении происходит поэлементное умножение каждого элемента строки или столбца на соответствующий элемент диагональной матрицы.
- Умножение диагональной матрицы на вектор — при умножении диагональной матрицы на вектор, каждый элемент вектора умножается на соответствующий элемент диагональной матрицы. Это позволяет улучшить алгоритмы машинного обучения и обработки сигналов.
Диагональные матрицы широко применяются в различных областях науки и техники, таких как линейная алгебра, теория вероятностей, статистика и др. Их свойства позволяют упростить математические вычисления и повысить эффективность алгоритмов.
Примеры диагональных матриц
Пример 1:
Рассмотрим следующую матрицу:
3 0 0 0 4 0 0 0 5
Эта матрица является диагональной, так как все элементы вне главной диагонали равны нулю.
Пример 2:
Рассмотрим следующую матрицу:
2 0 0 0 0 6 0 0 0 0 1 0 0 0 0 9
Эта матрица также является диагональной, так как все элементы вне главной диагонали равны нулю.
Диагональные матрицы часто встречаются в различных областях математики, таких как линейная алгебра и численные методы. Они имеют ряд особенностей и свойств, которые делают их полезными для решения различных задач и применений.
Применение диагональных матриц
Использование в линейной алгебре
Диагональные матрицы широко применяются в линейной алгебре. Они играют важную роль при решении систем линейных уравнений и нахождении собственных значений и собственных векторов матриц. Благодаря простой структуре диагональных матриц, операции с ними выполняются более эффективно, чем с обычными матрицами.
Применение в физике и технике
В физике и технике диагональные матрицы используются для описания линейных систем и моделирования динамических процессов. Они находят применение в анализе электрических цепей, механических систем, квантовой механике и других областях. Диагональные матрицы позволяют упростить математическую модель, ускорить вычисления и получить более точные результаты.
Примечание: диагональные матрицы также широко используются в компьютерной графике для преобразования координат и в других областях, где требуется быстрое и эффективное умножение матриц.
Умножение диагональных матриц
Пусть у нас есть две диагональные матрицы A и B размером n x n. Для умножения этих матриц мы будем использовать следующий алгоритм:
- Создадим пустую матрицу C размером n x n.
- Умножим каждый элемент i-ой строки i-го столбца матрицы A на соответствующий элемент i-ой строки i-го столбца матрицы B и запишем результат в элемент i-ой строки i-го столбца матрицы C.
- Повторим шаг 2 для всех i-х строк и i-х столбцов.
Итак, чтобы получить элемент Cij (элемент i-ой строки j-го столбца) матрицы C, мы будем умножать элементы Aik (элемент i-ой строки k-го столбца) матрицы A и Bkj (элемент k-ой строки j-го столбца) матрицы B и суммировать их для всех k от 1 до n. Таким образом, получаем следующую формулу для элемента Cij:
Cij = Ai1 * B1j + Ai2 * B2j + … + Ain * Bnj
Пример умножения диагональных матриц
Рассмотрим пример умножения двух диагональных матриц:
A =
| 2 0 0 | | 0 -1 0 | | 0 0 3 |
B =
| 4 0 0 | | 0 2 0 | | 0 0 -1 |
Для умножения матриц A и B мы поэлементно умножим соответствующие элементы и получим матрицу C:
C =
| 2*4 0 0 | | 0 -1*2 0 | | 0 0 3*-1 |
=
| 8 0 0 |
| 0 -2 0 |
| 0 0 -3 |
Таким образом, результатом умножения матриц A и B является матрица C:
C =
| 8 0 0 | | 0 -2 0 | | 0 0 -3 |
Умножение диагональных матриц — это простая операция, которая может быть выполнена эффективно, поскольку большинство элементов в каждой матрице равны нулю.
Обратная диагональная матрица
Обратная матрица – это такая матрица, умножение которой на исходную матрицу даёт единичную матрицу. Обратная матрица существует только у некоторых матриц, таких как квадратные матрицы, у которых определитель не равен нулю.
Обратная диагональная матрица – это диагональная матрица, у которой каждый элемент обратен к соответствующему элементу исходной матрицы. Другими словами, элементы обратной диагональной матрицы получаются путем взятия обратного значения к элементам главной диагонали исходной матрицы.
Обратная диагональная матрица играет важную роль в линейной алгебре и математическом анализе. Она используется в задачах определения обратной матрицы, решении систем линейных уравнений и других математических преобразованиях.
Диагональная матрица и системы линейных уравнений

Диагональные матрицы обладают рядом интересных свойств, которые находят применение в решении систем линейных уравнений. Система линейных уравнений — это набор уравнений, в которых все неизвестные переменные входят в линейной форме и должны быть решены одновременно.
Решение системы линейных уравнений с диагональной матрицей
При решении системы линейных уравнений с диагональной матрицей можно использовать простой и эффективный метод. Такая система может быть записана в виде:
a₁₁x₁ + a₁₂x₂ + … + a₁ₙxₙ = b₁
a₂₁x₁ + a₂₂x₂ + … + a₂ₙxₙ = b₂
…
aₘ₁x₁ + aₘ₂x₂ + … + aₘₙxₙ = bₘ
Где a₁₁, a₁₂, …, aₘₙ — элементы диагональной матрицы, x₁, x₂, …, xₙ — неизвестные переменные, b₁, b₂, …, bₘ — свободные члены уравнений.
Для решения системы линейных уравнений нужно разделить каждое уравнение на соответствующий элемент диагонали, получив систему вида:
x₁ = b₁/a₁₁
x₂ = b₂/a₂₂
…
xₙ = bₙ/aₙₙ
Применение диагональной матрицы в системах линейных уравнений
Диагональные матрицы часто встречаются при решении систем линейных уравнений. Их основное преимущество заключается в том, что решение системы линейных уравнений с диагональной матрицей сводится к простым арифметическим операциям.
Кроме того, диагональная матрица имеет обратную матрицу, которая также является диагональной. Это упрощает процесс обратного преобразования и позволяет быстро находить решения систем линейных уравнений.
Таким образом, диагональные матрицы являются важным инструментом при решении систем линейных уравнений, обладают рядом полезных свойств и позволяют производить эффективные вычисления.
Вопрос-ответ:
Какие свойства имеют диагональные матрицы?
Диагональная матрица — это матрица, у которой все элементы, находящиеся вне главной диагонали, равны нулю. Главная диагональ состоит из элементов, находящихся на пересечении строки и столбца с равными номерами. Свойства диагональных матриц включают коммутативность умножения, ассоциативность умножения, возможность сложения и вычитания диагональных матриц, а также возможность обращения диагональных невырожденных матриц.
Верно ли, что диагональная матрица всегда квадратная?
Да, в общем случае диагональная матрица является квадратной. Это означает, что количество строк совпадает с количеством столбцов. Однако, в теории матриц существуют также прямоугольные диагональные матрицы, у которых количество строк не равно количеству столбцов. В практических задачах чаще всего используются квадратные диагональные матрицы.
Как вычислить обратную матрицу для диагональной матрицы?
Обратная матрица для диагональной невырожденной матрицы может быть вычислена путем взятия обратных значений элементов главной диагонали и оставления нулей на месте остальных элементов. Если же хотя бы один элемент главной диагонали равен нулю, то матрица называется вырожденной, и у нее нет обратной матрицы.
Какие преобразования можно совершить с диагональной матрицей?
С диагональными матрицами можно совершать такие преобразования, как умножение на число, сложение и вычитание. При умножении диагональной матрицы на число, все элементы главной диагонали просто умножаются на это число, а остальные элементы остаются неизменными. При сложении или вычитании двух диагональных матриц, аналогично, складываются или вычитаются только элементы главной диагонали, а остальные элементы остаются неизменными.
Что такое диагональная матрица?
Диагональная матрица — это матрица, у которой все элементы, не лежащие на главной диагонали, равны нулю. То есть все элементы, которые находятся на пересечении строки и столбца с одним и тем же номером, отличные от нуля. Все остальные элементы матрицы равны нулю.