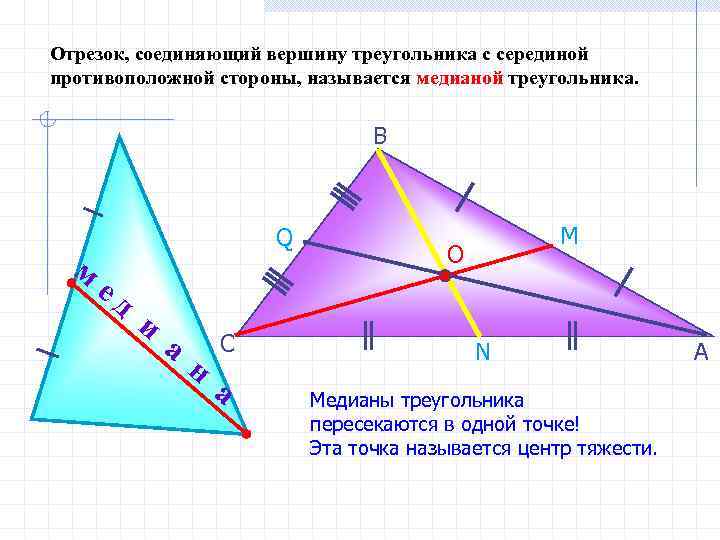
Медианой треугольника. Медиана проходит через вершину треугольника и делит противоположную сторону на две равные части. Это важное геометрическое понятие, которое используется в разных областях науки и техники.
Медиана также позволяет найти середину отрезка. Для этого достаточно провести медиану из вершины треугольника и точку пересечения этой медианы с противоположной стороной будет являться серединой этого отрезка.
Что такое отрезок, соединяющий вершину треугольника с серединой противоположной стороны?
Медиана делит сторону треугольника на две равные части и проходит через середину этой стороны. Одна из важных особенностей медианы заключается в том, что она пересекает другие медианы в одной точке, которая называется центром масс треугольника или точкой пересечения медиан.
Медианы обладают интересными свойствами. Например, длина каждой медианы равна половине длины соответствующей противоположной стороны треугольника. Также медианы делят площадь треугольника на шесть равных треугольников.
Медианы являются ключевым элементом в геометрических и численных аспектах треугольников, и их свойства широко применяются в различных математических и инженерных приложениях.
Определение и свойства

Свойство 1: Равенство
Все медианы в треугольнике пересекаются в одной точке, которая называется центром тяжести или барицентром. Это означает, что длины трех медиан равны между собой.
Свойство 2: Деление
Каждая медиана делит площадь треугольника пополам. То есть, если обозначить длину стороны треугольника как a, то площадь треугольника равна S = (a * m) / 2, где m — длина любой медианы.
Медианы также являются важными элементами в треугольниках по другим причинам, например, в связи с нахождением центра окружности, вписанной в треугольник, или определением площади треугольника при помощи формулы Герона.
Зависимость отрезка от типа треугольника
Отрезок, который соединяет вершину треугольника с серединой противоположной стороны, имеет разные свойства в зависимости от типа треугольника.
В разностороннем треугольнике, у которого все стороны и углы разные, отрезок, называемый медианой, соединяет любую вершину с серединой противоположной стороны. Медиана делит другие две стороны в отношении 2:1. То есть, отрезок от середины стороны до вершины равен двум отрезкам от середины стороны до точек пересечения медиан с этими сторонами.
В равнобедренном треугольнике, у которого две стороны и два угла равны между собой, отрезок, называемый высотой, соединяет вершину с противоположной стороной. Высота перпендикулярна этой стороне и делит ее пополам. Таким образом, длина высоты равна половине длины противоположной стороны.
В равностороннем треугольнике, у которого все стороны равны между собой, отрезок, называемый медианой, соединяет любую вершину с серединой противоположной стороны. В таком треугольнике все медианы равны между собой и делят другие медианы и стороны на отношение 2:1.
В итоге, зависимость отрезка от типа треугольника заключается в разных пропорциях, в которых отрезок делит стороны треугольника. Эти пропорции могут быть использованы для решения различных геометрических задач.
| Тип треугольника | Отрезок | Пропорция |
|---|---|---|
| Разносторонний | Медиана | 2:1 |
| Равнобедренный | Высота | 1:1 |
| Равносторонний | Медиана | 2:1 |
Геометрическое представление
Медиана треугольника — это линия, проходящая через вершину треугольника и пересекающая противоположную сторону в ее середине.
Когда медиана проведена, она делит этот отрезок пополам, образуя две равные части. Каждая из этих частей равна половине длины противоположной стороны треугольника.
Геометрическое представление такого отрезка иллюстрирует связь между вершинами треугольника и серединами его сторон, а также демонстрирует симметрию между этими элементами треугольника.
Использование в практике
Такой отрезок, называемый медианой, является линией симметрии треугольника и делит его на две равные части по площади. Медиана также проходит через середины других сторон треугольника и пересекается в одной точке, называемой центром тяжести треугольника.
Использование медиан в практике может быть разнообразным. Например, в архитектуре и строительстве медианы используются для определения точек равновесия и распределения нагрузки при проектировании и строительстве зданий. Кроме того, медианы находят применение в медицине при расчете идеальной величины дозировки лекарств и определении точек наибольшей концентрации вещества в организме.
В математическом моделировании и компьютерной графике медианы используются для определения точек пересечения и точек экстремумов, что позволяет строить более точные и реалистичные модели.
Также медианы применяются в геодезии и навигации для определения точек нахождения объектов, а также для построения полей равноудаленности и определения кратчайших путей.
Пример использования медианы:
Рассмотрим пример практического применения медианы в архитектуре. При проектировании многоэтажного здания необходимо определить оптимальное распределение нагрузки, чтобы избежать перекосов и неустойчивости. В этом случае медиана, соединяющая вершину здания с серединой противоположной стороны, позволяет равномерно распределить нагрузку и достичь стабильности конструкции.
Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, известный как медиана, имеет огромное значение в различных областях практики, таких как архитектура, строительство, медицина, компьютерная графика и другие. Знание и использование медианы позволяют решать разнообразные задачи, связанные с определением равновесия, распределением нагрузки, точек пересечения и многими другими.
Формула для вычисления отрезка
Важно отметить, что медиана треугольника делит противоположную сторону на два равных отрезка. Используя эту информацию, можно вывести формулу для вычисления отрезка медианы треугольника.
Формула
Формула для вычисления отрезка медианы треугольника имеет вид:
м = 1/2 * √(2 * а^2 + 2 * b^2 — c^2)
Где:
- м — длина отрезка медианы треугольника
- а, b, c — длины сторон треугольника
Таким образом, используя данную формулу, можно вычислить длину отрезка медианы треугольника с помощью длин его сторон.
Примеры решения задач
Для решения задач, связанных с отрезками, соединяющими вершины треугольника с серединами противоположных сторон, необходимо применять геометрические законы и свойства. Рассмотрим несколько примеров:
Пример 1:
Дан треугольник ABC, где AB = 8 см, BC = 6 см и AC = 10 см. Найдем длину отрезка, соединяющего вершину A с серединой противоположной стороны.
Сначала найдем середину стороны BC. Для этого сложим координаты точек B и C, разделим полученную сумму на 2 и получим координаты середины:
xM = (xB + xC) / 2 = (0 + 6) / 2 = 3
yM = (yB + yC) / 2 = (0 + 0) / 2 = 0
Таким образом, середина стороны BC имеет координаты (3, 0).
Затем найдем уравнение прямой, проходящей через вершину A и середину стороны BC. Для этого используем формулу прямой:
y — yA = ((yM — yA) / (xM — xA)) * (x — xA)
Подставим известные значения:
y — 0 = ((0 — yA) / (3 — xA)) * (x — xA)
Упростим уравнение:
y = (-(yA / (3 — xA))) * (x — xA)
Теперь найдем уравнение прямой, проходящей через вершины B и C. Для этого используем аналогичную формулу прямой:
y — yB = ((yC — yB) / (xC — xB)) * (x — xB)
Подставим известные значения:
y — 0 = ((0 — 0) / (6 — 0)) * (x — 6)
Упростим уравнение:
y = (0 / 6) * (x — 6) = 0
Таким образом, получим систему уравнений:
y = (-(yA / (3 — xA))) * (x — xA)
y = 0
Решим систему уравнений и найдем точку пересечения прямых. Полученные координаты будут являться серединой стороны AC и вершиной треугольника A:
… (продолжение статьи)
Значимость отрезка в тригонометрии
В тригонометрии, отрезок, соединяющий вершину треугольника с серединой противоположной стороны, играет важную роль. Он называется медианой треугольника и обозначается как М.
Медиана является одной из трех существенных линий, проходящих через вершины треугольника. Остальные две линии — высота и биссектриса.
Особенностью медианы является то, что она делит треугольник на две равные площади. Если треугольник ABC имеет медиану AM, то площадь треугольника ABM будет равна площади треугольника ACM. Это свойство становится полезным при решении различных задач в тригонометрии, так как позволяет связать стороны и углы треугольника с его высотой.
Медиана также играет ключевую роль в определении центра тяжести треугольника. Центр тяжести — точка, в которой пересекаются все три медианы треугольника. Он является геометрическим центром треугольника и обладает рядом интересных свойств.
Значение медианы в вычислениях
Медианы используются в различных тригонометрических вычислениях. Одно из наиболее распространенных применений медиан — вычисление размеров треугольника. Зная длину медианы и другие данные о треугольнике, можно определить длины его сторон, площадь и высоту.
Медианы также используются в построении различных фигур и нахождении их параметров. Например, при построении медианного треугольника, все три медианы пересекаются в одной точке — центре тяжести. Это позволяет построить треугольник с заданными размерами и расположением.
Таким образом, отрезок, соединяющий вершину треугольника с серединой противоположной стороны, имеет значительное значение в тригонометрии. Он не только связывает различные стороны и углы треугольника, но и используется в вычислениях и построении геометрических фигур.
Вопрос-ответ:
Что такое отрезок, который соединяет вершину треугольника с серединой противоположной стороны?
Отрезок, который соединяет вершину треугольника с серединой противоположной стороны, называется медианой.
Чем отличается медиана треугольника от других его сторон?
Медиана треугольника соединяет вершину с серединой противолежащей стороны и делит ее пополам. Она отличается от других сторон тем, что она всегда проходит через середины других двух сторон треугольника.
Зачем нужна медиана треугольника?
Медиана треугольника является важным элементом в геометрических вычислениях. Она помогает определить центр масс треугольника, удобна для нахождения точек пересечения, а также используется в некоторых задачах и теоремах геометрии.
Как вычислить длину медианы треугольника?
Длину медианы треугольника можно вычислить с помощью формулы: m = (2/3) * sqrt(2 * b^2 + 2 * c^2 — a^2), где m — длина медианы, а a, b, c — длины сторон треугольника.
Является ли медиана треугольника отрезком с фиксированной длиной?
Нет, медиана треугольника не является отрезком с фиксированной длиной. Ее длина зависит от длин сторон треугольника и может быть различной для разных треугольников.