Точка отрезка делящая его пополам называется

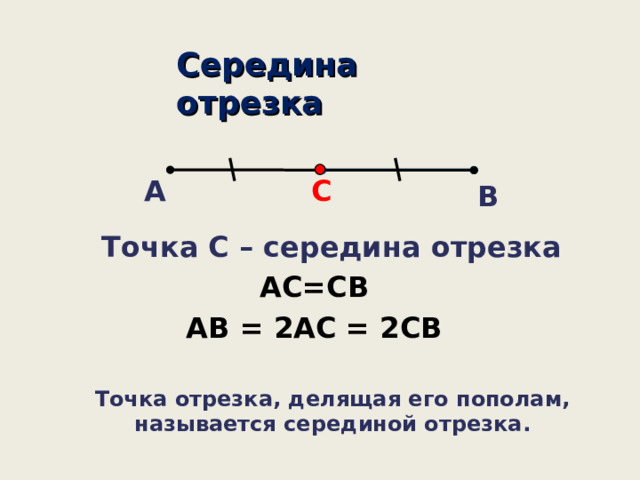
Один из важных понятий в математике и геометрии – точка отрезка, делящая его пополам. Это особенное положение точки на отрезке, которое делит его на две равные части. Точка, которая делит отрезок пополам, называется серединой или медианой отрезка.

Середина отрезка является особенной точкой, так как она находится на равном удалении от его концов. Поэтому, если мы возьмем две линейки и положим их от концов отрезка до середины, то оба участка отрезка будут иметь одинаковую длину. Можно сказать, что середина отрезка является его математическим центром.

Понятие середины отрезка активно используется в различных областях математики, физики и геометрии. В геометрии, середина отрезка играет важную роль при построении перпендикуляров, средних линий и центров симметрии фигур. В физике, середина отрезка может быть использована для расчета момента инерции тела или поиска центра масс.

Содержание

Что такое точка отрезка?

Для нахождения точки отрезка можно воспользоваться формулой:

Формула	Описание
x = (x1 + x2) / 2	Нахождение координаты x точки отрезка
y = (y1 + y2) / 2	Нахождение координаты y точки отрезка

Где (x1, y1) и (x2, y2) — координаты концов отрезка.

Точка отрезка является важным понятием в математике и геометрии. Она используется для различных расчетов и приложений, таких как построение графиков, определение середины отрезка и нахождение нужных точек на отрезке.

Понятие точки отрезка

Для того чтобы найти точку отрезка, необходимо выразить её координаты с использованием формулы. Пусть отрезок AB задан координатами точек A(x1, y1) и B(x2, y2). Тогда координаты точки отрезка M можно найти по формуле:

Координаты точки отрезка:

x_M = (x₁ + x₂) / 2

y_M = (y₁ + y₂) / 2

Таким образом, координаты точки M являются средними арифметическими координат точек A и B.

Пример:

Пусть точка A имеет координаты A(2, 4), а точка B имеет координаты B(6, 8). Чтобы найти координаты точки отрезка M, подставим значения в формулу:

x_M = (2 + 6) / 2 = 8 / 2 = 4

y_M = (4 + / 2 = 12 / 2 = 6

Таким образом, точка отрезка M имеет координаты M(4, 6).

Примеры точек отрезка

Точка O делит отрезок AB пополам, если расстояние от A до O равно расстоянию от O до B.
Например, если отрезок AB имеет концы в точках A (5,7) и B (9,11), то точка O (7,9) будет делить его пополам.
Точка O также может быть находиться в любом другом месте на отрезке AB и все равно делить его пополам.
Например, если отрезок AB имеет концы в точках A (-2,3) и B (4,9), то точка O (1,6) также будет делить его пополам.
Всего существует бесконечное количество точек, которые могут делить отрезок пополам.

Отрезки и их деление

Деление отрезка

Деление отрезка заключается в поиске точки, которая разделяет его на две равные части. Такая точка называется точкой деления и обозначается буквой «М».

Для нахождения точки деления отрезка его длина делится пополам.

Формула нахождения точки деления

Пусть отрезок имеет начальную точку «A» с координатами (x₁, y₁) и конечную точку «B» с координатами (x₂, y₂). Точка деления «М» находится по формуле:

x_М = (x₁ + x₂) / 2

y_М = (y₁ + y₂) / 2

Таким образом, координаты точки деления «М» равны средним значениям координат начальной и конечной точек отрезка.

Найденная точка деления разделяет отрезок на две равные по длине части.

Точка, делящая отрезок пополам

Математически, точка, делящая отрезок пополам, называется серединой отрезка. Обозначается этой точкой и находится на его середине. Другими словами, расстояние от начала отрезка до середины равно расстоянию от середины до конца отрезка.

Середина отрезка является важным понятием в геометрии и имеет множество применений. Она используется, например, для построения перпендикуляров, нахождения центра окружности, определения равенства отрезков и решения различных задач на среднюю линию треугольника. Знание положения середины отрезка помогает в различных геометрических расчетах и конструкциях.

Способы определения такой точки

Существуют различные способы определения точки, которая делит отрезок пополам:

Геометрический способ. Для определения точки, делящей отрезок пополам, можно построить перпендикулярную серединному перпендикуляру и найти их точку пересечения.
Алгебраический способ. Используя координаты концов отрезка, можно найти точку, делящую его пополам, с помощью формулы:
x_{середины} = (x₁ + x₂) / 2

y_{середины} = (y₁ + y₂) / 2
Вычислительный способ. С помощью программы или калькулятора можно вычислить координаты точки, разделяющей отрезок пополам, посредством выполнения алгоритма нахождения средней точки отрезка.

Эти способы позволяют определить точку, делящую отрезок пополам, с высокой точностью и эффективностью.

Геометрическое представление

Геометрическое представление точки отрезка, делящей его пополам, основано на применении геометрических понятий и конструкций.

Для нахождения точки, делящей отрезок пополам, можно использовать следующий алгоритм:

Находится середина отрезка, которая является точкой пересечения его концов.
Эта середина делит отрезок на две равные части и является искомой точкой.

Таким образом, геометрически представление точки, делящей отрезок пополам, связано с понятием середины отрезка и его делимости на две равные части.

Математические вычисления

Основные математические операции:

Сложение — операция, которая позволяет складывать два или более числа. Результатом сложения является сумма.
Вычитание — операция, которая позволяет вычитать одно число из другого. Результатом вычитания является разность.
Умножение — операция, которая позволяет умножать одно число на другое. Результатом умножения является произведение.
Деление — операция, которая позволяет делить одно число на другое. Результатом деления является частное.

Другие важные понятия:

Десятичная система счисления — система, в которой числа записываются с использованием десяти разрядов (от 0 до 9).
Десятичная дробь — число, которое записывается после запятой в десятичной системе счисления.
Проценты — доля от целого, которая выражается в виде сотых долей. Проценты широко используются для выражения отношений и расчетов скидок, налогов и т. д.

Математические вычисления являются основой для решения сложных задач и позволяют получить точные, надежные результаты. Они применяются в научных исследованиях, физике, экономике, информатике, инженерии и многих других областях. Понимание математических вычислений позволяет развивать логическое мышление и решать сложные задачи на постоянной основе.

Вопрос-ответ:

Как называется точка, которая делит отрезок пополам?

Точка, которая делит отрезок пополам, называется серединой отрезка.

Каким образом можно найти точку, делящую отрезок пополам?

Чтобы найти точку, делящую отрезок пополам, необходимо определить среднюю точку отрезка, применив формулу, которая находит среднее значение координат точек отрезка.

Как можно использовать понятие точки, делящей отрезок пополам, в геометрии?

Понятие точки, делящей отрезок пополам, широко используется в геометрии. Например, оно может быть применено для нахождения центра масс системы точек, разделения отрезков на равные части, определения равенства треугольников и многих других геометрических задач.

Есть ли какие-то особенности точки, делящей отрезок с ограниченными координатами?

Если отрезок имеет ограниченные координаты, то его середина также будет иметь координаты в пределах этих ограничений. Например, если отрезок задан на плоскости с координатами [-5, 5], то середина этого отрезка будет иметь координаты в диапазоне от -5 до 5 по обеим осям.