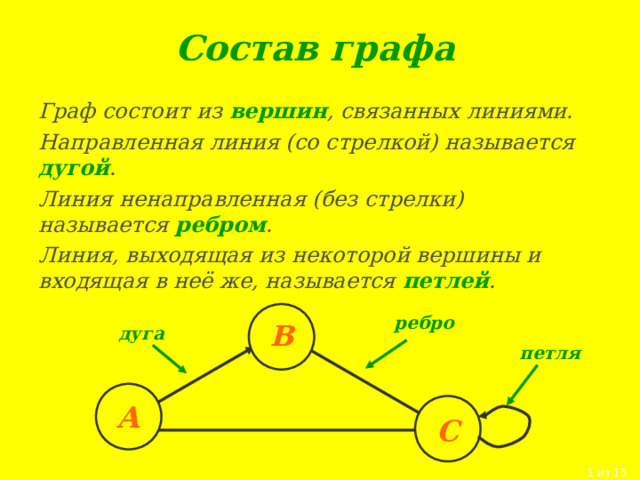
Граф – это абстрактная математическая структура, которая представляет собой множество вершин, соединенных дугами. Каждая дуга соединяет две вершины и может быть направленной или не направленной, в зависимости от характера связи между вершинами. Графы являются часто используемыми моделями в различных областях науки, техники и информатики.
Вершина графа — это отдельный элемент графа, который может быть представлен как узел, точка или объект. Вершины соединяются дугами и образуют ребра графа. Каждая вершина может иметь свое уникальное имя, которое помогает идентифицировать ее в контексте графа. Число вершин в графе может быть разным — от нескольких до бесконечности.
Таким образом, граф, вершины которого соединены дугами, называется ориентированным или неориентированным графом соответственно, в зависимости от того, есть ли направленность у дуг. Ориентированный граф имеет направление на дуги, что означает, что движение по графу возможно только в определенном направлении. Неориентированный граф не имеет направления на дуги и позволяет переходить между вершинами в обоих направлениях.
Что такое граф?
Графы используются для моделирования различных явлений и задач в разных областях, таких как компьютерные науки, транспорт, социология, биология и другие. Они являются удобным инструментом для представления сложных взаимосвязей и позволяют анализировать их с помощью различных алгоритмов.
В графе каждая вершина может быть связана с одной или несколькими другими вершинами с помощью ребер. Если ребра направлены, то граф называется ориентированным. Если же ребра не имеют направления, то граф называется неориентированным.
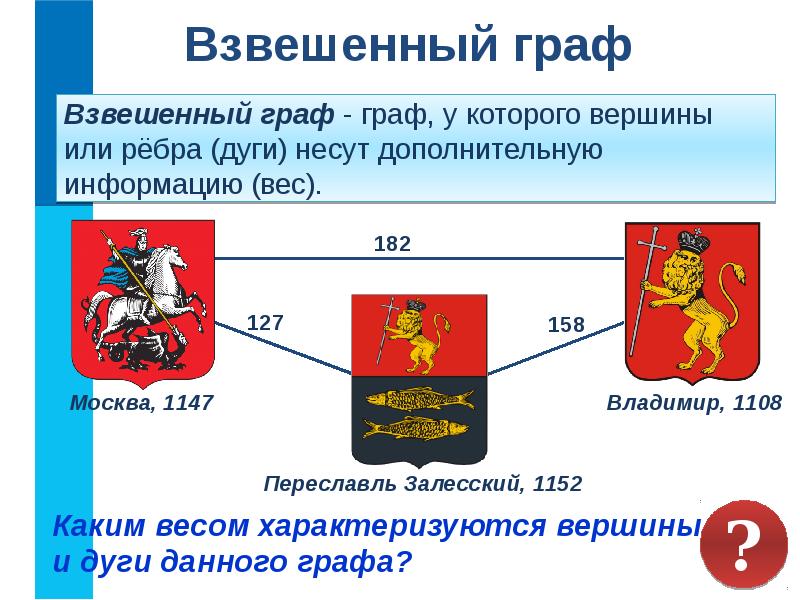
Графы могут быть разных типов в зависимости от наличия или отсутствия определенных свойств. Например, граф может быть связным, если существует путь от любой вершины к любой другой вершине. Или граф может быть ациклическим, если в нем нет циклов. Также графы могут быть взвешенными, когда каждому ребру приписывается некоторая числовая характеристика или вес.
Одной из основных задач при работе с графами является поиск путей или кратчайших путей между вершинами. Для этого используются различные алгоритмы, такие как поиск в глубину, поиск в ширину, алгоритм Дейкстры и другие.
- Примеры применения графов в реальной жизни:
- Маршрутизация в компьютерных сетях.
- Анализ социальных связей в социологии и маркетинге.
- Моделирование дорожной сети в транспортной инженерии.
- Представление семантических связей между словами в лингвистике.
- Расчет кратчайшего пути для доставки товаров в логистике.
Таким образом, граф — это мощный инструмент для представления и анализа связей между объектами или событиями. Он является фундаментальной структурой данных, которая находит применение во многих областях и играет важную роль в различных алгоритмах и задачах.
Понятие графа и его описание
Вершины графа обычно представляют собой какие-либо объекты или сущности, а ребра — отношения или связи между этими объектами. Граф может быть направленным, когда ребра имеют определенное направление, или ненаправленным, когда ребра не имеют направления.
Описание графа включает в себя перечисление всех вершин и их связей с помощью ребер. Вершины обычно обозначаются числовыми или буквенными метками, а ребра — парой вершин, которые они соединяют. Для удобства описание графа может быть представлено в виде таблицы, где каждая строка таблицы соответствует ребру, а столбцы — вершинам, которые оно соединяет.
| Вершины | Ребра |
|---|---|
| A | (A, B) |
| B | (B, C) |
| C | (C, A) |
В данном примере граф состоит из трех вершин (A, B и C) и трех ребер (A — B, B — C и C — A). Это описание позволяет наглядно представить связи между вершинами графа.
Вершины и дуги графа
Вершины графа – это отдельные элементы, которые могут быть связаны друг с другом. Каждая вершина может иметь некоторые атрибуты и свойства, которые определяют ее характеристики. Например, в графе, представляющем города и дороги между ними, каждая вершина может представлять отдельный город и иметь атрибуты, такие как название, координаты или население.
Дуги графа служат для соединения вершин и указывают на наличие какого-то отношения или связи между вершинами. Каждая дуга может иметь свои атрибуты, которые определяют ее свойства. Например, в графе, представляющем социальную сеть, каждая дуга может представлять связь между пользователями и содержать информацию о типе связи или времени установления.
Вершины и дуги графа могут иметь различные типы, в зависимости от задачи или контекста, в котором используется граф. Например, в ориентированном графе дуги имеют направление, указывающее на порядок, в котором вершины связаны. В неориентированном графе дуги не имеют направления и связывают вершины без учета порядка.
Пример использования графа
Один из примеров, где графы широко используются, – это маршрутизация в компьютерных сетях. Каждый узел сети (компьютер или маршрутизатор) представляется вершиной графа, а соединения между узлами – дугами. Такой граф может быть использован для определения оптимального пути передачи данных от отправителя к получателю.
Графы также используются в алгоритмах машинного обучения, где каждый объект или сущность представляется вершиной графа, а связи между ними – дугами. Такой граф может быть использован для анализа структуры данных и поиска зависимостей между объектами.
Использование графов позволяет эффективно решать различные задачи в разных областях, благодаря их гибкости и универсальности. Понимание вершин и дуг графа является важным ключом для работы с этой структурой данных и проведения различных анализов.
Граф с соединенными дугами
Графом называется абстрактная структура данных, представляющая собой множество вершин, соединенных дугами. При этом, графы различаются по количеству дуг и их направленности.
Направленные и ненаправленные графы
Графы могут быть как направленными, так и ненаправленными. В направленном графе дуги имеют определенное направление, указывающее на то, что вершина A соединена с вершиной B, но не наоборот. В ненаправленном графе, дуги соединяют вершины без указания направления.
Свойства графа с соединенными дугами
Граф с соединенными дугами имеет следующую структуру:
| Вершины | Дуги |
|---|---|
| Вершина 1 | Дуга 1 |
| Вершина 2 | Дуга 2 |
| … | … |
Вершины графа обозначают различные объекты или сущности, а дуги представляют собой связи между этими объектами. Дуги могут быть взвешенными или безвесными, что означает наличие или отсутствие у каждой дуги числового значения (веса).
Графы с соединенными дугами широко используются в различных областях, таких как компьютерная наука, теория графов, социальные сети и др. Они позволяют описывать и анализировать сложные системы, взаимосвязи между объектами и принимать решения на основе анализа и моделирования структуры графа.
Что такое вершина графа?
Вершины графа могут быть использованы для представления различных объектов или сущностей, таких как города на карте, компьютерные узлы в сети, пользователи в социальной сети или любые другие соединенные между собой объекты или сущности.
Графы, состоящие из вершин и ребер, являются важными инструментами, используемыми для моделирования и анализа сложных систем. Они позволяют наглядно представлять связи и взаимодействия между различными элементами, а также исследовать и анализировать различные свойства и характеристики графа, такие как связность, направленность, вес ребер и другие.
Выбор вершин и их соединений в графе может иметь существенное значение для решения конкретной задачи или определенной цели. Поэтому понимание вершин и их роли в графе является важным аспектом при работе с графовыми структурами и их анализом.
Определение вершины и ее свойства
Вершиной графа называется элементарный объект, который обычно обозначается буквой или числом. Она представляет собой точку или узел, в котором сходятся ребра графа. Вершины в графе могут быть представлены различными объектами или сущностями, например, городами на карте или узлами в компьютерной сети.
У вершины графа есть несколько свойств и характеристик, которые определяют ее поведение и роль в графе. Вот некоторые из них:
| Свойство | Описание |
|---|---|
| Степень | Количество ребер, смежных с данной вершиной. Входящая степень — количество входящих ребер, исходящая степень — количество исходящих ребер. |
| Соседи | Список вершин, смежных с данной. Вершины, соединенные ребрами с данной вершиной. |
| Графовая метка | Дополнительная информация, которая может быть назначена вершине для удобства организации и обработки графа. |
Вершины в графе играют важную роль, так как именно они описывают объекты и связи между ними. Они помогают анализировать и представлять сложные системы или сети в удобном и понятном виде.
Соединение вершин графа
Для создания связей между вершинами в графе используются дуги. Дуга представляет собой направленное ребро, которое соединяет одну вершину с другой. Вершина, из которой выходит дуга, называется начальной вершиной, а вершина, в которую входит дуга, — конечной вершиной. Направление дуги указывает на то, какая вершина является начальной, а какая — конечной.
Соединение вершин графа может быть однонаправленным или двунаправленным в зависимости от наличия направления дуги. В случае однонаправленного соединения дуга идет только от начальной к конечной вершине, а в случае двунаправленного соединения дуга идет как от начальной вершины к конечной, так и наоборот.
Параметры соединения вершин
Соединение вершин графа может иметь различные параметры, которые определяют его характеристики. Основные параметры соединения вершин:
| Параметр | Описание |
|---|---|
| Вес | Показывает степень важности или длину пути между вершинами. Используется для определения кратчайшего пути в графе. |
| Пропускная способность | Определяет максимальное количество информации или ресурсов, которое может пройти через соединение за единицу времени. Используется в сетевых графах. |
| Стоимость | Выражает затраты или затраты на использование соединения. Используется в оптимизационных задачах. |
Знание о параметрах соединения вершин позволяет анализировать и оптимизировать граф, а также применять его в различных областях, таких как транспортные сети, социальные сети, логистика и т.д.
Что такое дуга графа?
Дуга графа представляет собой направленное ребро, которое связывает две вершины графа между собой. Дуга имеет начальную и конечную вершины, и обозначается стрелкой, указывающей направление её перехода. Она позволяет передвигаться от одной вершины к другой в определенном направлении.
Дуги играют важную роль в описании различных видов графов, таких как ориентированные графы, графы с взвешенными рёбрами и сетевые графы. Они могут использоваться для представления различных связей и отношений между объектами или событиями, например в системе дорог, логистической сети, социальном графе и т.д.
При работе с дугами графа важно учитывать их направление, так как оно определяет порядок перемещения между вершинами. В некоторых случаях дуги могут иметь веса, которые отражают стоимость или пропускную способность перехода. Это позволяет учесть различные факторы при анализе и обработке графов.
Изучение дуг графа и их свойств играет важную роль в теории графов и различных областях, включая компьютерные науки, транспортную логистику, социальные науки и другие. Обладая пониманием дуг и их роли в графах, мы можем эффективно анализировать, моделировать и решать различные задачи, связанные с сетями и связанными системами.
Роль дуги в графе
Одна из основных ролей дуги в графе — представление отношения или связи между вершинами. Она показывает, какая вершина связана с другой и в каком направлении можно перемещаться от одной вершины к другой.
Дуги также могут использоваться для представления веса или стоимости связи между вершинами. Например, в весовом графе дуга может иметь числовое значение, которое указывает на стоимость перехода от одной вершины к другой. Это позволяет рассчитывать оптимальные пути или находить кратчайший путь между вершинами.
Дуги также могут быть использованы для представления потока информации или передачи данных в графе. В этом случае дуги могут иметь разную пропускную способность или вместимость, что позволяет моделировать передачу данных по сети или поток информации между устройствами.
Кроме того, дуги могут использоваться для моделирования различных видов отношений, таких как родитель-ребенок, следование или зависимость. Например, в дереве дуги могут представлять собой связи между родительской и дочерней вершиной, показывая иерархию.
В целом, роль дуги в графе заключается в объединении вершин и представлении их связей и отношений. Благодаря дугам мы можем анализировать и моделировать различные виды систем, связей и процессов, представленных в виде графов.
Вопрос-ответ:
Что такое граф в терминах математики?
Граф — это абстрактная математическая модель, используемая для представления сетей связей между объектами.
Как называется вершина в графе?
Вершина в графе называется точкой, узлом или углом.
Что означает дуга в графе?
Дуга в графе представляет собой связь между двумя вершинами. Она может быть направленной или ненаправленной.
Как называется граф, вершины которого соединены дугами?
Такой граф называется ориентированным графом или диграфом.
Какие основные типы графов существуют?
Существуют ориентированные и неориентированные графы. Ориентированный граф — это граф, в котором дуги имеют направление, а неориентированный граф — это граф, в котором дуги не имеют направления.