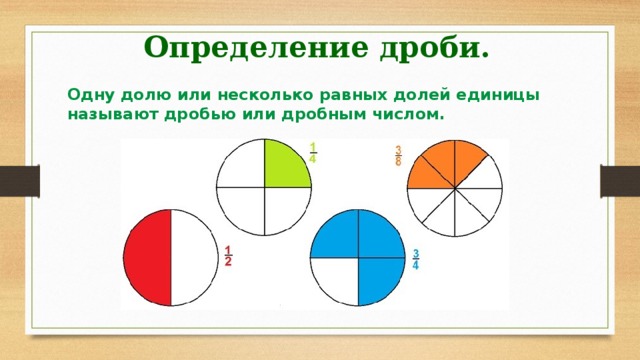
Положительные рациональные числа – это числа, которые могут быть представлены в виде дробей со знаменателем, не равным нулю, и числителем, который может быть любым натуральным числом.
Дробь – это математический объект, представляющий собой отношение двух чисел – числителя и знаменателя. Числитель – это верхняя часть дроби, которая указывает на количество единиц, а знаменатель – это нижняя часть дроби, которая указывает на количество частей на, которые число разделено.
Для того чтобы дробь была положительной и рациональной, числитель должен быть больше или равен нулю, а знаменатель должен быть больше нуля. Если числитель равен нулю, то дроби называются равными нулю. Если числитель меньше нуля, то дробь будет отрицательной и может быть представлена как положительная дробь с отрицательным числителем.
Что такое положительное рациональное число дробью?
Положительные рациональные числа дробью часто используются для измерения величин, которые могут быть разделены на равные части. Например, если у нас есть торт, который разделен на 8 равных частей, и мы возьмем 3 из них, то мы можем выразить это как положительное рациональное число дробью: 3/8.
Положительные рациональные числа дробью также могут быть представлены в виде десятичной дроби. Например, 1/2 в десятичном представлении будет равно 0.5, а 3/4 — 0.75.
Однако важно помнить, что положительные рациональные числа дробью не ограничиваются только десятичным представлением. Они могут быть представлены в различных форматах, таких как смешанные числа, проценты и т. д.
Важно отметить, что положительные рациональные числа дробью отличаются от отрицательных рациональных чисел дробью, где числитель или знаменатель могут быть отрицательными, или от иррациональных чисел, которые не могут быть выражены в виде дроби.
Определение положительного рационального числа

Пример:
1/2, 5/3, 7/8 — все эти числа являются положительными рациональными числами.
Положительные рациональные числа можно представить на числовой оси в интервале от 0 до бесконечности справа от нуля. Они могут быть как конечными (например, 1/2 или 3/4), так и бесконечными (например, 2/3 или 5/7). Каждое положительное рациональное число может быть представлено несколькими дробями, так как дробь можно сократить до несократимой формы.
Важно помнить:
- Положительные рациональные числа являются одной из частей множества рациональных чисел, которое включает в себя как положительные, так и отрицательные числа.
- Они можно использовать для описания различных величин, таких как доли, проценты, коэффициенты увеличения или уменьшения, вероятности и т.д.
Знание и понимание положительных рациональных чисел является важным компонентом в широком спектре математических и прикладных наук, а также имеет практическое применение в повседневной жизни.
Понятие дроби и ее структура
Структура дроби
Дробь состоит из двух основных частей: числителя и знаменателя. Числитель указывает, сколько частей целого числа имеется, а знаменатель определяет, на сколько частей разделено целое число.
Числитель и знаменатель могут быть положительными или отрицательными целыми числами. Они состоят из цифр и могут быть представлены как натуральные числа (1, 2, 3, …), нуль (0) или отрицательные целые числа (-1, -2, -3, …).
В дроби числитель обычно записывается над знаменателем и разделен чертой. Например: 3/4. Это означает, что имеется 3 части из 4.
Пример: Дробь 5/8 представляет отношение 5 частей к 8 частям целого числа.
Также, дробь может быть представлена в виде смешанной дроби, которая состоит из целой части и правильной дроби. Например: 3 1/2.
Дробь может быть сокращена, если числитель и знаменатель имеют общие делители, которые можно убрать. Результат сокращения – простая дробь, у которой числитель и знаменатель взаимно просты (у них нет общих делителей, кроме 1).
Понимание понятия дроби и ее структуры важно для работы с числами, выполняемых математических операций и решения различных задач в повседневной жизни и научных областях.
Числитель и знаменатель дроби
Дробь представляет собой математическую конструкцию, которая состоит из двух чисел: числителя и знаменателя. Числитель указывает на количество частей, на которые нужно разделить целое число, а знаменатель определяет, на сколько равных частей нужно разделить целое число.
Числитель обозначается верхней частью дроби, а знаменатель — нижней. Например, в дроби 3/4 числитель равен 3, а знаменатель равен 4.
Числитель и знаменатель могут быть как положительными, так и отрицательными числами. Положительный знаменатель говорит о том, что части дроби больше единицы, а отрицательный знаменатель обозначает, что части дроби меньше единицы. Например, в дроби -2/3 числитель равен -2, а знаменатель равен 3.
Числа, представленные числителем и знаменателем, могут быть как целыми, так и десятичными, зависит от контекста. Для работы с дробями используются особые правила, включая операции сложения, вычитания, умножения и деления.
Как определить положительность рационального числа
1. Если числитель и знаменатель имеют одинаковые знаки (оба положительные или оба отрицательные), то рациональное число является положительным.
2. Если числитель и знаменатель имеют разные знаки (один положительный и один отрицательный), то рациональное число является отрицательным.
3. Если числитель равен нулю, то рациональное число считается равным нулю и не имеет знака (не положительное и не отрицательное).
4. Если знаменатель равен нулю, то такая дробь считается неопределенной и не имеет положительного или отрицательного значения.
Важно отметить, что при выполнении арифметических операций с рациональными числами их положительность может изменяться.
Примеры положительных рациональных чисел в дробной форме
Пример 1: 3/4
В этом примере числитель равен 3, а знаменатель равен 4. Дробь 3/4 является положительным рациональным числом, так как она больше нуля.
Пример 2: 5/2
В этом примере числитель равен 5, а знаменатель равен 2. Дробь 5/2 также является положительным рациональным числом, так как она больше нуля.
Таким образом, примеры положительных рациональных чисел в дробной форме включают дроби типа 3/4 и 5/2 и т.д.
Как представить положительное рациональное число десятичной дробью
Положительное рациональное число может быть представлено в виде десятичной дроби, которая состоит из целой части и дробной части. Чтобы представить число в виде десятичной дроби, нужно разделить его на 10, 100, 1000 и т.д. в зависимости от количества десятичных разрядов.
Процесс представления числа в виде десятичной дроби можно представить следующим образом:
- Определите количество цифр в дробной части числа.
- Разделите число на 10 в степени, соответствующей количеству цифр в дробной части.
- Полученное число будет иметь десятичную дробь, где целая часть будет равна нулю, а дробная часть будет соответствовать остатку.
Например, если у нас есть число 5/2, то мы можем представить его в виде десятичной дроби следующим образом:
- Дробная часть числа — 2.
- Разделим число на 10 в степени 1 (так как дробная часть состоит из одной цифры).
- Получаем 2/10, что равно 0.2.
Таким образом, число 5/2 представлено в виде десятичной дроби 0.2. Аналогично, любое положительное рациональное число можно представить в виде десятичной дроби, следуя вышеуказанным шагам.
Использование положительных рациональных чисел в реальной жизни
Одной из областей, где положительные рациональные числа наиболее активно используются, является финансовая сфера. Например, когда мы совершаем покупку в магазине, цена товара может быть выражена с помощью положительного рационального числа. Дробной частью этого числа может быть цена за грамм или миллилитр товара, а целая часть — количество грамм или миллилитров товара, который мы покупаем.
Еще одним примером использования положительных рациональных чисел в реальной жизни является строительство. При проектировании и расчете конструкций, инженеры используют дроби для определения необходимого количества материала, точности измерений и распределения нагрузки на конструкцию.
Кроме того, положительные рациональные числа используются в науке и технике для описания физических величин, таких как скорости, температуры и массы. Например, при изучении движения тела насколько оно быстрое можно выразить с помощью положительных рациональных чисел, где числитель будет обозначать пройденное расстояние, а знаменатель — время, затраченное для преодоления этого расстояния.
Таким образом, положительные рациональные числа имеют широкое применение в реальной жизни и используются в различных сферах, включая финансы, строительство, науку и технику. Они помогают нам точно описывать и измерять различные физические и математические явления, а также принимать обоснованные решения в повседневной жизни.
Вопрос-ответ:
Что такое положительное рациональное число?
Положительным рациональным числом называется число, которое может быть представлено в виде обыкновенной дроби, где числитель и знаменатель являются целыми числами и знаменатель не равен нулю. При этом числитель и знаменатель могут быть как положительными, так и отрицательными числами, но результат дроби всегда будет положительным числом.
Можно ли отрицательным числом быть положительным рациональным числом?
Нет, положительное рациональное число всегда положительно. Отрицательное число дробь называется отрицательным рациональным числом.
Какие числа могут быть представлены в виде обыкновенной дроби?
Все числа, которые можно представить в виде обыкновенной дроби, называются рациональными числами. Это включает в себя как положительные, так и отрицательные числа.
Как проверить, является ли число положительным рациональным числом?
Чтобы проверить, является ли число положительным рациональным числом, необходимо убедиться, что оно может быть представлено в виде обыкновенной дроби, где числитель и знаменатель являются целыми числами и знаменатель не равен нулю. Если это условие выполняется, то число является положительным рациональным числом.