
Арифметические выражения — это математические выражения, которые состоят из чисел, операций и скобок. Они используются для описания арифметических операций, таких как сложение, вычитание, умножение и деление.
Арифметические выражения могут быть простыми или сложными, в зависимости от количества и сложности операций, которые они содержат. Примеры простых арифметических выражений включают «2 + 3», «4 * 5» и «10 / 2». Более сложные выражения могут включать комбинации операций и скобок, например, «(2 + 3) * 4» или «3 * (4 + 2)».
Арифметические выражения широко используются в математике, программировании и других областях, где требуется выполнение математических операций. Они используются для вычисления значений и решения задач, связанных с числами и операциями над ними.
Определение арифметического выражения
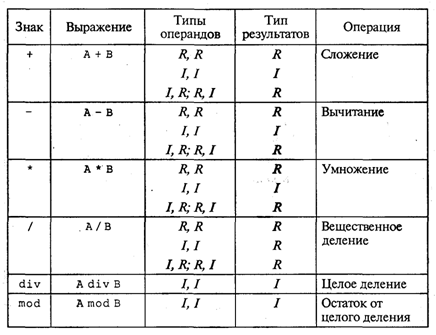
Арифметическое выражение может содержать следующие элементы:
- Числа — это значения, используемые в вычислениях. Например, числа 1, 2, 3 и т. д.
- Переменные — это символы, представляющие неизвестные или изменяющиеся значения. Например, переменные x, y, z и т. д.
- Арифметические операции — это действия, выполняемые над числами и переменными. Например, сложение (+), вычитание (-), умножение (*), деление (/), и т. д.
- Скобки — используются для установления порядка выполнения операций. Например, выражение (2 + 3) * 4 будет иметь разные значения, если скобки будут применяться по-разному, то есть 2 + (3 * 4) и (2 + 3) * 4.
Арифметическое выражение может быть простым, состоящим из одной операции, или сложным, состоящим из нескольких операций и вложенных скобок.
Основные элементы арифметического выражения
Арифметическое выражение представляет собой комбинацию чисел и математических операций, которые выполняются в определенном порядке. Оно состоит из следующих основных элементов:
1. Числа
Числа — это основные составные элементы арифметического выражения. Они могут быть целыми или десятичными числами. В выражении может быть как одно число, так и несколько чисел, объединенных операциями.
2. Операции
Операции представляют собой действия, выполняемые над числами. В арифметическом выражении можно использовать следующие операции:
- Сложение (+) – операция, при которой два числа складываются.
- Вычитание (-) – операция, при которой из одного числа вычитается другое.
- Умножение (*) – операция, при которой два числа перемножаются.
- Деление (/) – операция, при которой одно число делится на другое.
- Степень (**) – операция, при которой число возводится в указанную степень.
Операции в арифметическом выражении могут быть объединены в комплексные выражения с использованием скобок или приоритета операций.
Пример арифметического выражения:
3 + 5 * (7 — 2) / 4 ** 2
В данном выражении числа 3 и 5 объединены операцией сложения, числа 7 и 2 объединены операцией вычитания, а затем результат умножается на 5. Полученное значение делится на 4, а затем возводится в квадрат.
Арифметические операции в выражении
В арифметике выражение представляет собой комбинацию чисел и операций над ними. Арифметические операции выполняются в определенном порядке, который определяется приоритетом операций. В выражении можно использовать следующие арифметические операции:
- Сложение (+) — операция сложения двух чисел.
- Вычитание (-) — операция вычитания одного числа из другого.
- Умножение (*) — операция умножения двух чисел.
- Деление (/) — операция деления одного числа на другое.
- Возведение в степень (^) — операция возведения числа в заданную степень.
- Модуль (%) — операция нахождения остатка от деления одного числа на другое.
При написании выражений важно соблюдать правила порядка операций. В первую очередь выполняются операции в скобках, затем операции возведения в степень, после этого умножение и деление, и, наконец, сложение и вычитание.
Например, выражение 2 + 3 * 4 будет вычислено следующим образом: сначала будет выполнено умножение чисел 3 и 4, что даст 12, и затем будет выполнено сложение числа 2 и полученного результата 12, что даст итоговый результат равный 14.
В выражениях также можно использовать скобки для явного указания порядка выполнения операций. Например, выражение (2 + 3) * 4 будет вычислено следующим образом: сначала будет выполнено сложение чисел 2 и 3, что даст 5, а затем будет выполнено умножение числа 5 и числа 4, что даст итоговый результат равный 20.
При работе с арифметическими операциями важно учитывать правила округления и обработки ошибок при делении на ноль. Также следует помнить о приоритетности операций и использовании скобок для явного задания порядка выполнения операций в выражении.
Порядок выполнения операций в выражении
Порядок выполнения операций в выражении определяется следующими правилами:
- Скобки: операции, заключенные в скобки, выполняются первыми.
- Умножение и деление: операции умножения и деления выполняются перед операциями сложения и вычитания.
- Сложение и вычитание: операции сложения и вычитания выполняются в последнюю очередь.
Если в выражении присутствуют операции одного приоритета, они выполняются слева направо.
С помощью скобок можно изменить порядок операций. Выражение внутри самых внешних скобок будет выполнено первым.
Использование скобок позволяет упростить выражение и явно указать порядок выполнения операций. Оно также помогает избежать ошибок при интерпретации выражения.
Знание правил порядка выполнения операций позволяет правильно вычислить значение арифметического выражения и получить точный результат.
Примеры арифметических выражений
Арифметическое выражение представляет собой комбинацию чисел, операций и скобок, в которых выполняются математические операции. Вот несколько примеров арифметических выражений:
Пример 1:
Выражение: 2 + 3 * 4
Решение: Сначала выполняется умножение, затем сложение.
Результат: 14
Пример 2:
Выражение: (5 — 2) * 8
Решение: Вычитание в скобках выполняется первым, затем умножение.
Результат: 24
Пример 3:
Выражение: 10 / (4 — 2)
Решение: Вычитание в скобках выполняется первым, затем деление.
Результат: 5
В этих примерах показаны различные операции (сложение, вычитание, умножение, деление) и использование скобок для указания порядка операций. Арифметические выражения могут быть намного более сложными и содержать большее количество операций и чисел.
Для более подробного изучения арифметических выражений и их решения можно обратиться к учебникам по математике или использовать онлайн-ресурсы и калькуляторы с функцией решения выражений.
| Операция | Пример | Результат |
|---|---|---|
| Сложение | 2 + 3 | 5 |
| Вычитание | 5 — 2 | 3 |
| Умножение | 3 * 4 | 12 |
| Деление | 10 / 2 | 5 |
Преобразование выражений
Преобразование выражений может включать в себя использование следующих методов:
- Факторизация — разложение выражения на множители для упрощения его формы и сокращения.
- Раскрытие скобок — преобразование выражения, содержащего скобки, путем распределения операций на множители внутри скобок.
- Перегруппировка — изменение порядка сложения или умножения операндов внутри выражения.
- Упрощение — преобразование выражения с использованием свойств арифметических операций для сокращения его длины или сложности.
- Замена переменных — замена одной или нескольких переменных на другие, чтобы упростить или решить выражение.
Преобразование выражений является важной и полезной математической техникой, которая помогает улучшить понимание и решение математических задач.
Вопрос-ответ:
Что такое арифметическое выражение?
Арифметическое выражение — это математическая запись, в которой используются числа, операции и знаки, определенные для конкретных операций. Примеры арифметических выражений: 2 + 3, 5 * (4 — 2), 10 / (2 + 3).
Какие операции могут входить в арифметическое выражение?
В арифметическом выражении могут быть использованы следующие операции: сложение (+), вычитание (-), умножение (*), деление (/), возведение в степень (^), взятие остатка от деления (%), а также скобки для определения порядка выполнения операций.
Можно ли использовать переменные в арифметических выражениях?
Да, в арифметических выражениях можно использовать переменные. Переменная — это символ, обозначающий неизвестное значение. Примеры использования переменных в арифметических выражениях: x + 5, 2 * y — 3.
Как определить порядок выполнения операций в арифметическом выражении?
В арифметическом выражении порядок выполнения операций определяется с учетом приоритета операций. Обычно умножение и деление имеют более высокий приоритет, чем сложение и вычитание. Если в выражении есть скобки, то операции внутри скобок выполняются первыми.