
Математика – это наука о числах и их взаимоотношениях. В ней есть множество операций, которые позволяют нам выполнять различные вычисления. Одним из таких важных действий являются умножение и деление.
При умножении мы складываем число столько раз, сколько указывает множитель. Результирующее число называется произведением. В математике для обозначения произведения мы используем знак умножения — «×».
Произведение числа на 1 равно самому числу. Это нейтральный элемент умножения, который не изменяет число. Однако, умножение на 0 даёт 0. В этом случае, любое число умноженное на 0 равно 0.
А что касается деления, то здесь всё немного сложнее. Деление – это обратная операция умножению. Она позволяет нам разделить число на указанное количество частей. Процесс деления представляет собой подсчёт, сколько раз делитель содержится в нашем числе. Результирующее число называется частным, а число, которое мы делим, – делимым.
Если же мы делаем деление на 0, то результатом будет бесконечность. В математике бесконечность также обозначается специальным символом – ∞.
Числа в умножении
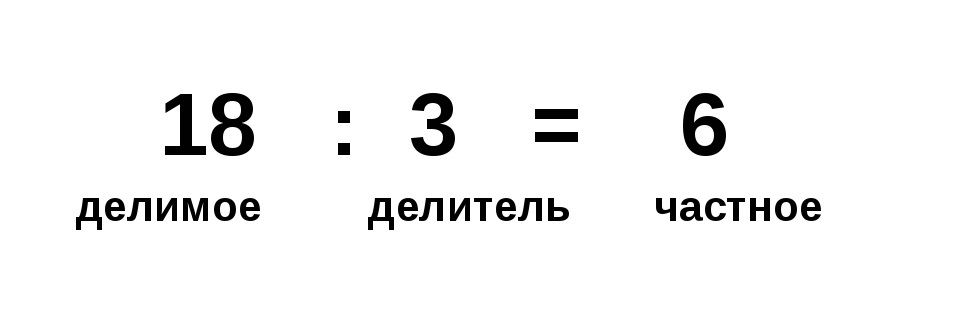
Множитель
Множитель — это число, которое участвует в умножении и определяет количество повторений или соединений другого числа. Множитель может быть как положительным, так и отрицательным.
Множимое
Множимое — это число, которое умножается на множитель и определяет, сколько повторений или соединений будет в результате умножения.
Умножение может быть представлено в виде таблицы, известной как таблица умножения. В таблице умножения пересекаются множители, и в каждой ячейке таблицы указывается произведение соответствующих множителей. Такая таблица позволяет быстро находить произведение двух чисел.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 2 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 |
| 3 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 |
| 4 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 |
| 5 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 |
| 6 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 |
| 7 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 |
| 8 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 |
| 9 | 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 |
Числа в умножении имеют свои особенности и свойства, которые помогают в решении различных задач с использованием умножения. Знание этих свойств позволяет более эффективно выполнять умножение и применять его в реальных ситуациях.
Множимое
Важно помнить, что при умножении, множимые могут быть как положительными, так и отрицательными числами. Например, в выражении «3 * 4 = 12», число «3» является множимым. В случае, если множимое отрицательное, знак минуса также учитывается при вычислении произведения.
Множимые могут быть различной природы — это могут быть целые числа, десятичные дроби, бесконечные числа или даже переменные в алгебраических выражениях. Умножение множимых производится по определенным правилам, установленным в математике. Знание множимых и их свойств позволяет эффективно работать с уравнениями и решать разнообразные задачи.
Множитель
Множитель может быть положительным, отрицательным или нулем. Если множитель положителен, результат умножения будет больше нуля. Если множитель отрицателен, результат умножения будет меньше нуля. Умножение на ноль дает ноль.
Например, в уравнении 2 * 3 = 6, число 2 является множителем, а число 3 — множимым. Результатом умножения двух чисел будет 6.
В математике умножение называется операцией коммутативным, что означает порядок множителей не имеет значения. Например, 2 * 3 и 3 * 2 дадут один и тот же результат 6.
Множители также используются в делении. В выражении 6 / 2 = 3, число 6 является делимым, а число 2 является делителем. Результатом деления двух чисел будет 3.
Использование правильных множителей в умножении и делении является важным аспектом решения математических задач и применения математики в повседневной жизни.
Произведение
Умножение — это одна из основных арифметических операций. Оно используется для повторения сложения одного числа на протяжении определенного количества раз. Например, чтобы посчитать произведение 5 × 3, нужно прибавить 5 к самому себе 3 раза: 5 + 5 + 5 = 15.
Произведение может быть коммутативным, то есть порядок множителей не имеет значения. Например, 2 × 3 = 3 × 2 = 6. Однако, произведение не является ассоциативным, то есть порядок вычисления имеет значение. Например, (2 × 3) × 4 = 6 × 4 = 24, но 2 × (3 × 4) = 2 × 12 = 24.
Важно помнить, что произведение нуля на любое число всегда равно нулю: 0 × x = 0, где x — любое число. Также результатом деления нуля на любое число будет ноль: 0 ÷ x = 0, где x — любое число, кроме нуля.
В случае умножения или деления дробных чисел, результат также будет дробным числом. Например, 2.5 × 0.5 = 1.25 или 4 ÷ 2 = 2.
Операция деления также является обратной к умножению. Если произведение двух чисел равно третьему числу, то деление этого числа на одно из множителей дает другой множитель. Например, 4 × 5 = 20, поэтому 20 ÷ 4 = 5 и 20 ÷ 5 = 4.
| Пример | Произведение |
|---|---|
| 2 × 3 | 6 |
| 3.5 × 2 | 7 |
| 0 × 5 | 0 |
| 2.5 × 0.5 | 1.25 |
| 20 ÷ 4 | 5 |
Числа в делении
Вычисление частного в делении включает в себя следующие числа:
Делимое — число, которое необходимо разделить на другое число.
Делитель — число, на которое делится делимое.
Частное — результат деления, значение, которое получается при делении делимого на делитель.
Для обозначения операции деления часто используется символ «/» или горизонтальная черта. Например, 10/2 или 10÷2 означает, что число 10 делится на число 2, и результатом будет число 5.
Важно помнить, что в делении существует также понятие остатка. Если деление некоторых чисел не происходит без остатка, то получается десятичная или обыкновенная дробь. Остаток от деления обозначается символом «%». Например, 10%3 означает, что при делении числа 10 на число 3 остаток будет равен 1.
При выполнении вычислений с числами, важно учитывать правила операций и приоритетность арифметических действий, чтобы получить корректный результат.
Делимое

Делимое играет важную роль в математике, особенно при решении задач, связанных с делением. Величина и значение делимого могут быть разными в зависимости от контекста или задачи.
Например, в выражении 10 ÷ 2 = 5, число 10 является делимым, так как оно будет разделено на число 2 без остатка. В этом случае частное равно 5.
Делимое может быть как положительным, так и отрицательным числом. В математике существуют правила и свойства, которые позволяют совершать операции с делимыми числами, чтобы получать правильные результаты.
Не следует путать делимое с результатом деления, который называется частным. Делимое — это число, которое делится, в то время как частное — это результат этого деления.
Важно понимать понятие делимого для успешного решения задач, связанных с делением, и для общего понимания математики.
Делитель
Делитель может быть любым числом, включая натуральные числа, целые числа, десятичные дроби и даже отрицательные числа.
При делении, делитель указывается справа от знака деления, который обозначается символом «/» или символом «:». Например, в выражении «12 / 4» число 4 является делителем числа 12.
Помимо использования делителей в математике, они также находят применение в других областях, таких как программирование, физика и экономика. В программировании, например, можно использовать делители для проверки делимости чисел или для определения остатка от деления.
Частное
Например, если у нас есть число 10 и мы делим его на число 2, то получаем частное равное 5. Это означает, что 10 разделить на 2 равно 5.
Другой пример: если у нас есть число 15 и мы делим его на число 3, то получаем частное равное 5. Это означает, что 15 разделить на 3 также равно 5.
Частное может быть как целым числом, так и десятичной дробью. Например, если у нас есть число 6 и мы делим его на число 4, то получаем частное равное 1.5.
Также стоит помнить, что если мы делим ноль на любое число, то получаем ноль в качестве частного.
Частное имеет несколько свойств, например:
- Если мы умножим частное на делитель, то получим делимое.
- Если мы умножим частное на результат деления, то получим делимое.
Примеры:
Пусть у нас есть делимое 8 и делитель 4. Тогда частное равно 2. Если мы умножим 2 на 4, то получим 8.
Пусть у нас есть делимое 12 и делитель 6. Тогда частное равно 2. Если мы умножим 2 на 6, то также получим 12.
Вопрос-ответ:
Что такое множители и произведение?
Множители — это числа, которые участвуют в операции умножения. Произведение — это результат умножения двух или более множителей.
Как называется число, которое делится на другое число без остатка?
Такое число называется «делитель». Например, если число 8 делится на число 2 без остатка, то 2 является делителем числа 8.
Что такое делимое и делитель?
Делимое — это число, которое делится на другое число без остатка. Делитель — это число, на которое делится делимое.
Что будет, если делитель равен нулю?
Если делитель равен нулю, то операция деления невозможна. Математический закон гласит, что на ноль делить нельзя.
Как называется число, которое является результатом деления одного числа на другое?
Это число называется «частное». Например, если число 10 делится на число 2, то 5 является частным от деления 10 на 2.
Что такое множители и произведение?
Множители – это числа, которые участвуют в операции умножения. Произведение – это результат умножения двух или более множителей.
Как называется число, которое делится на другое число?
Число, которое делится на другое число, называется делимым. А число, на которое делится другое число, называется делителем.