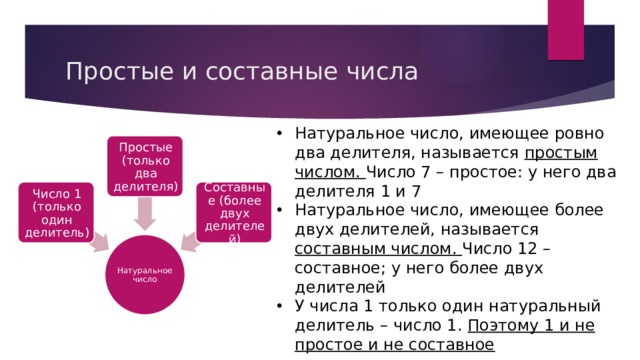
Математика – это удивительная наука, которая изучает числа и их свойства. Одно из самых интересных понятий в математике – это числа, которые имеют более двух делителей. Такие числа называются составными числами.
Составные числа отличаются от простых чисел, которые имеют только два делителя: 1 и само число. Например, числа 2, 3 и 5 являются простыми, потому что у них только два делителя – 1 и само число. Однако числа 4, 6 и 8 являются составными, так как они имеют больше двух делителей.
Составные числа можно разложить на простые множители, то есть на множители, которые сами являются простыми числами. Например, число 12 можно разложить на простые множители: 2 * 2 * 3. Таким образом, составное число 12 имеет три делителя: 1, 2 и 3.
Что такое простое число?
Простые числа важны в математике и имеют много применений в различных областях. Они используются в криптографии для создания защищенных алгоритмов шифрования. Также простые числа широко применяются в теории чисел и в различных алгоритмах.
Определение простого числа базируется на основных принципах теории чисел и является одним из ключевых понятий в математике. Изучение простых чисел помогает углубить понимание числовых систем и их свойств.
Простые числа и их свойства
Простые числа играют важную роль в математике и криптографии. Например, они используются для шифрования данных и создания надежных алгоритмов.
У простых чисел есть несколько интересных свойств:
- Простые числа можно определить по формуле «N простое, если оно не делится нацело ни на одно число от 2 до корня из N». То есть, чтобы проверить, является ли число простым, достаточно проверить его деление на все числа от 2 до корня из N.
-
Множество простых чисел бесконечно. Это было доказано Евклидом более двух тысячелетий назад. Евклид предложил способ построения нового простого числа на основе уже существующих простых чисел.
-
Простые числа равномерно распределены по числовой прямой. Это означает, что с увеличением числа N вероятность его простоты не уменьшается.
-
Простые числа отлично подходят для задач факторизации и поиска наибольшего общего делителя. Также они являются основой для различных алгоритмов в криптографии, таких как алгоритм RSA.
Примеры простых чисел
Вот несколько примеров простых чисел:
2 — это самое маленькое простое число, которое является единственным четным простым числом.
3 — это следующее простое число и является самым маленьким нечетным простым числом.
5 — это простое число, которое не делится нацело ни на какое другое число, кроме 1 и 5.
7 — это еще одно простое число, которое не имеет делителей, кроме 1 и 7.
11 — простое число, которое не делится нацело ни на какое другое число, кроме 1 и 11.
Простые числа имеют важное значение в различных областях математики, таких как криптография, алгоритмы и факторизация. Они также используются в создании псевдослучайных чисел.
Составные числа
Делители составных чисел могут быть как целыми числами, так и десятичными дробями. Это означает, что составные числа могут быть разложены на простые множители, которые могут повторяться несколько раз.
Например, число 12 является составным числом, потому что оно может быть разделено на 1, 2, 3, 4, 6 и 12. Его простые множители — 2 и 3 — соответственно, и число 12 можно записать в виде произведения этих простых множителей: 2 * 2 * 3.
Составные числа играют важную роль в теории чисел и математике в целом. Они используются, например, в криптографии для создания безопасных шифров и в факторизации чисел для решения сложных математических проблем.
Важно отличать составные числа от простых, поскольку они имеют разные свойства и могут быть использованы в разных математических операциях. Понимание составных чисел помогает лучше понять структуру и свойства чисел в целом.
Определение составных чисел
Составным числом называется натуральное число, имеющее больше двух делителей, то есть не являющееся простым числом.
Простым числом называется натуральное число, имеющее только два делителя: единицу и само число.
Например:
Число 6 является составным числом, так как кроме единицы и самого числа 6, оно делится также на 2 и 3. В отличие от этого, число 5 является простым числом, так как оно делится только на 1 и 5.
Классификация чисел на простые и составные имеет важное значение в теории чисел и является одной из основных тем изучения математики.
Примеры составных чисел
Составным числом называется число, которое имеет более двух делителей. Вот некоторые примеры составных чисел:
- 4 — это составное число, так как оно делится на 1, 2 и 4.
- 9 — также является составным числом, так как оно делится на 1, 3 и 9.
- 25 — это составное число, так как оно делится на 1, 5 и 25.
- 49 — также является составным числом, так как оно делится на 1, 7 и 49.
- 100 — это еще один пример составного числа, оно делится на 1, 2, 4, 5, 10, 20, 25, 50 и 100.
Таким образом, составные числа имеют множество делителей, включая 1 и само число. Они отличаются от простых чисел, которые имеют только два делителя — 1 и само число.
Вопрос-ответ:
Что такое число с более чем двумя делителями?
Число с более чем двумя делителями — это число, которое может делиться не только на 1 и на само себя, но и на другие натуральные числа.
Как называется число, которое имеет более двух делителей?
Число, которое имеет более двух делителей, называется составным числом.
Можно ли найти примеры чисел с более чем двумя делителями?
Да, конечно. Некоторыми примерами чисел с более чем двумя делителями являются 4, 6, 8, 9 и т.д. Эти числа могут делиться на разные натуральные числа, а не только на 1 и на себя.
Для чего нужно знать понятие чисел с более чем двумя делителями?
Знание понятия чисел с более чем двумя делителями может быть полезным при решении различных математических задач, в том числе при факторизации чисел, нахождении наименьшего общего кратного и т.д.