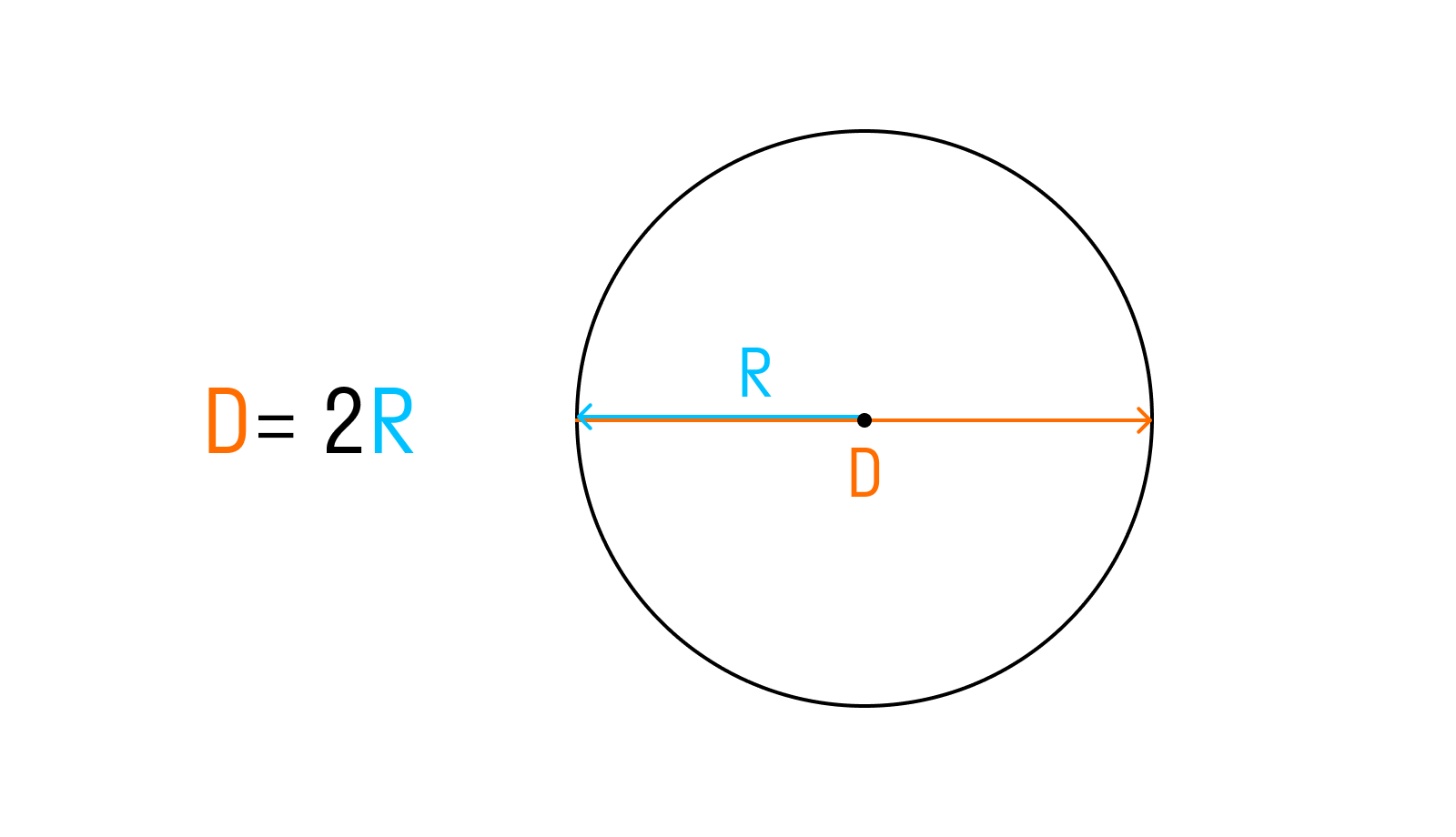
Окружность – это геометрическая фигура, которая представляет собой множество точек, расположенных на одной и той же плоскости и находящихся на одинаковом расстоянии от центра. Диаметр окружности – это отрезок, соединяющий две противоположные точки на этой окружности и проходящий через ее центр. Диаметр является одним из основных свойств окружности и имеет некоторые интересные неизменные характеристики.
Первое свойство, которым обладает диаметр окружности, – это то, что он является самой длинной хордой соединяющей две точки на окружности. Хорда – это отрезок, соединяющий две произвольные точки на окружности. Диаметр всегда будет иметь наибольшую длину среди всех хорд, проведенных на окружности, и ее значение будет равно удвоенной длине радиуса.
Второе свойство диаметра заключается в том, что он делит окружность на две половины, которые называются дугами. Дуга – это часть окружности, ограниченная двумя точками на окружности и соединяющая их кратчайшим путем. Когда диаметр делит окружность, образуются две равные дуги из всех дуг, которые можно получить на окружности. Это значит, что каждая дуга будет содержать по половине окружности.
Третье важное свойство диаметра окружности связано с его связью с радиусом. Радиус – это отрезок, соединяющий центр окружности с произвольной точкой на ее границе. Диаметр и радиус всегда связаны между собой таким образом, что диаметр будет равен удвоенному значению радиуса. То есть, радиус является половиной диаметра, и диаметр является удвоенной длиной радиуса.
Общая информация о диаметре окружности
| Свойство | Описание |
|---|---|
| Длина диаметра | Длина диаметра равна удвоенному радиусу окружности. Чтобы найти длину диаметра, умножьте радиус на 2. Формула для вычисления длины диаметра: L = 2r |
| Соотношение с другими свойствами окружности | Диаметр входит в ряд формул и соотношений, связанных с окружностью. Например, длина окружности связана с диаметром следующим образом: L = πd, где L — длина окружности, π — число Пи (примерно равное 3.14159), а d — диаметр. |
| Связь с понятием «радиус» | Диаметр связан с длиной радиуса окружности следующим образом: d = 2r, где d — диаметр, а r — радиус. Это означает, что радиус равен половине диаметра. |
| Диаметр как диагональ окружности | Диаметр также можно рассматривать как диагональ окружности, поскольку он проходит через центр и соединяет две противоположные точки на границе окружности. |
Таким образом, диаметр окружности является важным понятием, которое играет ключевую роль в разных аспектах геометрии и математики.
Что такое диаметр окружности
Свойства диаметра окружности:
- Диаметр является осью симметрии для окружности. Это означает, что если отразить окружность относительно диаметра, она останется неизменной.
- Каждая точка на окружности находится на равном расстоянии от диаметра.
- Диаметр делит окружность на две равные дуги.
- Длина диаметра выражается через радиус окружности по формуле: d = 2r, где d — длина диаметра, а r — радиус окружности.
- Диаметр окружности также определяет ее общую характеристику — ее длину. Формула для расчета окружности по диаметру выглядит следующим образом: L = πd, где L — длина окружности, π — число пи, а d — длина диаметра.
Знание и понимание диаметра окружности являются основой геометрии и позволяют применять его в различных математических и технических областях. Использование диаметра позволяет решать задачи по построению фигур, вычислению площадей и объемов, а также в конструировании и проектировании различных устройств и механизмов.
Формула для расчета диаметра окружности
Формула для расчета диаметра окружности выглядит следующим образом:
Д = 2 * R, где:
- Д — диаметр окружности
- R — радиус окружности
То есть, чтобы найти диаметр окружности, нужно умножить радиус на 2.
Например, если радиус окружности равен 5 сантиметров, то диаметр будет равен 10 сантиметров (2 * 5).
Основные свойства диаметра окружности
Основные свойства диаметра окружности:
- Диаметр – это отрезок, соединяющий две точки на окружности и проходящий через ее центр.
- Диаметр является наибольшей длиной отрезков, которые можно провести на окружности.
- Диаметр делит окружность на две равные дуги, называемые полуокружностями. Каждая полуокружность содержит по половине окружности и имеет длину, равную половине окружности.
- Диаметр является осью симметрии окружности. Если отразить окружность относительно ее диаметра, то получится идентичная окружность.
- Диаметр также используется для вычисления других свойств окружности, таких как радиус и длина окружности.
Эти свойства диаметра окружности помогают понять и использовать его значимость в различных математических и инженерных задачах, а также в анализе и моделировании геометрических объектов.
Связь диаметра с радиусом окружности
Связь между диаметром и радиусом окружности можно выразить простым математическим соотношением. Радиус окружности представляет собой половину диаметра, то есть радиус равен диаметру, деленному на 2.
Это соотношение можно записать следующим образом:
- Радиус = Диаметр / 2
Таким образом, зная значение диаметра окружности, можно легко вычислить радиус по формуле радиуса.
Связь между диаметром и радиусом является важным свойством окружности, которое позволяет выполнять различные геометрические вычисления и построения.
Расчет диаметра по радиусу окружности
Окружность и ее диаметр связаны соотношением: диаметр равен удвоенному радиусу.
Для расчета диаметра по заданному радиусу следует использовать следующую формулу:
Диаметр = 2 * Радиус
Например, если радиус окружности равен 5 см, то диаметр будет равен 10 см.
Зная диаметр окружности, можно вычислить ее площадь и длину. Площадь окружности равна π * (Диаметр/2)2, где π (пи) — это математическая константа, приближенное значение которой равно 3,14159. Длина окружности можно найти, применив формулу длина = π * Диаметр.
Диаметр и длина окружности
Диаметр является важным свойством окружности и имеет ряд интересных свойств:
- Диаметр окружности в два раза больше ее радиуса. То есть, если радиус равен R, то диаметр будет равен 2R.
- Через центр окружности можно провести бесконечное количество диаметров, и все они будут равны между собой.
- Длина диаметра можно вычислить по формуле: d = 2R, где d — длина диаметра, R — радиус окружности. Как видно, длина диаметра равна двум радиусам окружности.
Длина окружности — это длина замкнутой кривой, образованной окружностью. Она обозначается символом C или с помощью формулы «два радиуса, умноженные на число Пи», где R — радиус окружности, а π (пи) — математическая константа, которая приближенно равна 3.14159.
Длина окружности можно вычислить по формуле: C = 2πR, где C — длина окружности, R — радиус окружности.
Зная диаметр окружности, можно вычислить ее длину по формуле: C = πd, где C — длина окружности, d — диаметр окружности.
Диаметр и длина окружности взаимосвязаны и являются важными параметрами для решения геометрических задач и расчетов в различных областях науки и техники.
Как выразить длину окружности через диаметр
Длина окружности связана с ее диаметром особой формулой. Если мы знаем диаметр, мы можем легко найти длину окружности, применив следующую формулу:
Длина окружности = π * диаметр,
где π (пи) – это математическая константа, равная приблизительно 3,14159. Она используется для приближенного вычисления длины окружности.
Таким образом, если нам известен диаметр окружности, мы можем легко найти ее длину, умножив диаметр на π. Это простая и эффективная формула, которая широко применяется в геометрии, астрономии, физике и других науках.
Вопрос-ответ:
Что такое диаметр окружности?
Диаметр окружности — это отрезок, проходящий через центр окружности и соединяющий две точки на ее границе. Диаметр является наибольшей хордой окружности и равен удвоенному значению радиуса.
Как найти диаметр окружности, если известен ее радиус?
Для нахождения диаметра окружности по известному радиусу необходимо умножить значение радиуса на 2. То есть, диаметр равен двум радиусам. Формула для вычисления диаметра выглядит следующим образом: D = 2 * R.
Как связаны диаметр и окружность?
Диаметр и окружность тесно связаны между собой. Диаметр — это отрезок, проходящий через центр окружности и соединяющий две точки на ее границе. Диаметр является наибольшей хордой окружности. В свою очередь, окружность представляет собой замкнутую кривую линию, состоящую из всех точек на одинаковом расстоянии от центра. Таким образом, диаметр окружности является одной из основных характеристик окружности.
Что такое диаметр окружности?
Диаметр окружности — это отрезок, проходящий через центр окружности и соединяющий две точки ее периферии.
Как найти диаметр окружности, если известна ее длина?
Диаметр окружности можно найти, разделив ее длину на число π (пи).