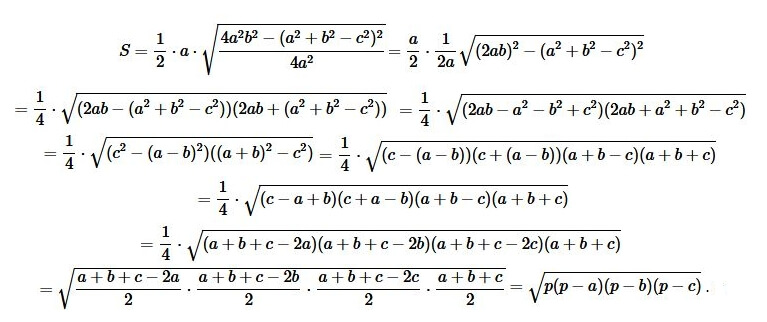
Формула Герона — одна из наиболее часто используемых формул в геометрии и математике, предназначенная для нахождения площади треугольника. Название формула получила в честь Дионисия Александрийского, который восстановил эту формулу в III веке до нашей эры. Формула Герона основана на длинах сторон треугольника и является методом, позволяющим найти площадь треугольника без использования высоты и углов.
Как пользоваться формулой Герона? Для использования формулы Герона необходимо знать длины всех трех сторон треугольника. Формула записывается следующим образом:
S = √(p(p-a)(p-b)(p-c))
Где S — площадь треугольника, p — полупериметр теругольника, a, b и c — длины сторон треугольника. Полупериметр вычисляется по формуле:
p = (a + b + c) / 2
После вычисления полупериметра треугольника, можно использовать его в формуле Герона для нахождения площади треугольника. Полученный результат будет выражен в единицах площади (например, квадратных метрах или квадратных сантиметрах), соответствующих используемым единицам измерения длины сторон треугольника.
Что такое Формула Герона и как ей пользоваться?
Формула Герона основана на полупериметре треугольника, который равен сумме длин всех его сторон, разделенной на 2. Используя эту величину, вычисляется площадь треугольника по следующей формуле:
| S = √(s * (s — a) * (s — b) * (s — c)) |
где S – площадь треугольника, s – полупериметр, a, b, c – длины сторон треугольника.
Для использования формулы Герона необходимо знать длины всех трех сторон треугольника. После этого, подставляем значения в формулу и выполняем все необходимые вычисления. В результате получаем площадь треугольника, выраженную в квадратных единицах.
Формула Герона позволяет вычислить площадь треугольника без необходимости знания его высоты. Это делает ее удобным инструментом для решения задач, связанных с геометрией и построением фигур.
Определение и назначение
Назначение формулы Герона заключается в том, чтобы дать точный и быстрый способ определить площадь треугольника, зная лишь длины его сторон. Это особенно полезно, когда недоступны другие методы измерения площади, например, при работе с картой или планом местности.
Формула Герона основана на полупериметре треугольника, который находится как сумма длин всех трех сторон, деленная на два:
S = sqrt(p * (p — a) * (p — b) * (p — c))
где S – площадь треугольника, a, b, c – длины сторон треугольника, а p = (a + b + c) / 2 – полупериметр.
С помощью этой формулы можно легко и быстро вычислить площадь треугольника по его сторонам, даже без необходимости знать его высоту или углы.
Формула для вычисления площади треугольника
Данная формула имеет следующий вид:
S = √(p · (p — a) · (p — b) · (p — c))
где:
- S – площадь треугольника;
- p – полупериметр треугольника, равный сумме длин всех его сторон, деленной на 2;
- a, b, c – длины сторон треугольника.
Чтобы использовать формулу Герона и вычислить площадь треугольника, необходимо знать длины всех его сторон. После этого можно вычислить полупериметр треугольника, затем подставить значения в формулу и выполнить вычисления.
Например, рассмотрим треугольник со сторонами длиной 5, 9 и 12. Сначала найдем полупериметр:
p = (5 + 9 + 12) / 2 = 13
Затем вычислим площадь, подставив значения в формулу:
S = √(13 · (13 — 5) · (13 — 9) · (13 — 12)) = √(13 · 8 · 4 · 1) = √416 = 20.396
Таким образом, площадь треугольника со сторонами 5, 9 и 12 равна 20.396 квадратных единиц.
Применение Формулы Герона в геометрии
Формула Герона имеет следующий вид:
S = √(p(p — a)(p — b)(p — c)),
где S — площадь треугольника, a, b, c — длины сторон треугольника, p — полупериметр треугольника, который вычисляется по формуле:
p = (a + b + c) / 2.
Применение формулы Герона особенно полезно, когда известны длины сторон треугольника, но отсутствует возможность определить высоту и основание для вычисления площади. Формула Герона позволяет найти площадь треугольника только по его сторонам.
Для использования формулы Герона необходимо знать длины всех трех сторон треугольника. Сначала вычисляем полупериметр треугольника — сумму длин всех сторон, деленную на 2. Затем вычисляем выражение под корнем в формуле Герона и извлекаем его квадратный корень. Полученное значение будет площадью треугольника.
Например, пусть у нас есть треугольник со сторонами a = 3, b = 4 и c = 5. Полупериметр треугольника равен:
p = (3 + 4 + 5) / 2 = 6.
Теперь мы можем вычислить площадь треугольника:
S = √(6(6 — 3)(6 — 4)(6 — 5)) = √(6 * 3 * 2 * 1) = √36 = 6.
Таким образом, площадь треугольника равна 6 единицам площади.
Формула Герона находит широкое применение в геометрии и позволяет быстро и удобно вычислять площадь треугольника, особенно в случаях, когда нет возможности использовать другие способы.
Как использовать Формулу Герона для вычисления площади треугольника?
Шаги для использования Формулы Герона:
- Измерьте длины всех трех сторон треугольника. Обозначим их как a, b и c.
- Вычислите полупериметр треугольника, который равен сумме всех сторон, деленной на 2. Формула для вычисления полупериметра: p = (a + b + c) / 2.
- Вычислите площадь треугольника, используя формулу Герона: S = √(p(p-a)(p-b)(p-c)), где S — площадь, а p — полупериметр треугольника.
Пример использования Формулы Герона:
- Допустим, у нас есть треугольник со сторонами длиной 4, 5 и 6.
- Вычисляем полупериметр: p = (4 + 5 + 6) / 2 = 7.5.
- Вычисляем площадь: S = √(7.5(7.5-4)(7.5-5)(7.5-6)) = √(7.5 * 3.5 * 2.5 * 1.5) = √(82.03125) ≈ 9.06.
Таким образом, площадь данного треугольника приближенно равна 9.06 квадратных единиц.
Формула Герона является удобным инструментом для вычисления площади треугольника, особенно когда неизвестна высота треугольника или углы треугольника. Она может быть полезной в различных областях, таких как геометрия, строительство и дизайн.
Понять значения всех сторон треугольника
Для понимания формулы Герона и вычисления площади треугольника по этой формуле необходимо знать значения всех его сторон. Стороны треугольника обозначаются буквами a, b и c.
Сторона a является основанием треугольника, к которому располагается высота. Сторона b и c — это боковые стороны треугольника. Для применения формулы Герона необходимо измерить длины всех трех сторон треугольника в одних и тех же единицах измерения, например в сантиметрах.
Значения сторон треугольника могут быть даны в условии задачи, измерены с помощью линейки или вычислены по теореме Пифагора или другим геометрическим методом.
Зная значения всех сторон треугольника, можно приступить к вычислению его площади с помощью формулы Герона.
| Сторона треугольника | Обозначение |
|---|---|
| Основание | a |
| Боковая сторона | b |
| Боковая сторона | c |
Вычислить полупериметр треугольника
Перед тем, как воспользоваться формулой Герона для вычисления площади треугольника, необходимо вычислить полупериметр.
Полупериметр треугольника — это сумма длин всех его сторон, разделенная на 2.
Чтобы вычислить полупериметр, необходимо знать длины всех трех сторон треугольника. Обозначим их соответственно как a, b и c.
Для вычисления полупериметра необходимо выполнить следующую формулу:
- Сложите длины всех трех сторон: a + b + c.
- Разделите получившуюся сумму на 2: (a + b + c) / 2.
Результат этого вычисления и будет значение полупериметра треугольника.
Полученное значение полупериметра можно затем использовать в формуле Герона для вычисления площади треугольника.
Применить Формулу Герона для вычисления площади
Чтобы применить Формулу Герона, нужно знать длины всех сторон треугольника. Предположим, у нас есть треугольник со сторонами a, b и c. Тогда площадь треугольника можно вычислить по следующей формуле:
S = √(p * (p — a) * (p — b) * (p — c))
где S — площадь треугольника, a, b и c — длины сторон, а p — полупериметр треугольника. Полупериметр вычисляется следующим образом:
p = (a + b + c) / 2
Итак, чтобы применить Формулу Герона для вычисления площади треугольника, нужно знать длины всех его сторон. Подставить значения сторон в формулу, вычислить полупериметр и найти квадратный корень от произведения разности полупериметра и каждой стороны треугольника. Полученный результат будет являться площадью треугольника.
Формула Герона позволяет вычислить площадь треугольника любой формы, если известны длины его сторон. Этот метод является эффективным и удобным для применения в практических задачах, связанных с геометрией и строительством.
Вопрос-ответ:
Что такое формула Герона?
Формула Герона — это математическая формула, которая позволяет вычислить площадь треугольника по длинам его сторон. Она была получена греческим математиком Героном.
Как выглядит формула Герона?
Формула Герона имеет вид: S = √(p(p — a)(p — b)(p — c)), где S — площадь треугольника, a, b, c — длины его сторон, p — полупериметр треугольника (сумма длин сторон, деленная на 2).
Зачем нужна формула Герона?
Формула Герона позволяет найти площадь треугольника, зная только длины его сторон, что делает ее очень полезной при решении различных геометрических задач.
Как пользоваться формулой Герона?
Чтобы воспользоваться формулой Герона, необходимо знать длины сторон треугольника. После этого нужно вычислить полупериметр треугольника, затем подставить все значения в формулу и выполнить несложные вычисления.
Есть ли какие-то примеры использования формулы Герона?
Да, конечно. Например, если у вас есть треугольник со сторонами длиной 5, 7 и 9, то вы можете найти его площадь с помощью формулы Герона: S = √(p(p — a)(p — b)(p — c)), где a = 5, b = 7, c = 9, а p = (5 + 7 + 9) / 2 = 21 / 2 = 10.5. Подставим значения и получим S = √(10.5(10.5 — 5)(10.5 — 7)(10.5 — 9)) = √(10.5 * 5.5 * 3.5 * 1.5) = √317.7 ≈ 17.83.
Что такое формула Герона?
Формула Герона — это формула, которая позволяет вычислить площадь треугольника, зная длины его сторон.