Объясните какая фигура называется ломаной геометрия 8 класс

Ломаная — одна из основных геометрических фигур, изучаемых в 8 классе. Она представляет собой линию, состоящую из конечного числа отрезков, которые могут быть прямолинейными или кривыми. Каждый из отрезков называется звеном ломаной. Важно отметить, что концы каждого звена ломаной соединены точками, и эти точки могут быть как начальными, так и конечными для других звеньев.

Ломаные часто встречаются в реальной жизни и используются для описания различных объектов и феноменов. Например, они могут представлять географические маршруты или траектории движения. Также ломаные находят применение в различных областях, включая архитектуру, дизайн, инженерию и картографию.

Изучение ломаных в геометрии связано с понятиями и свойствами углов, секущих и касательных линий, а также с тем, как ломаные могут быть классифицированы в зависимости от их формы и свойств. Знание и понимание этих понятий позволяет анализировать и строить ломаные, а также используется при решении задач на построение геометрических объектов.

Таким образом, знакомство с ломаными в геометрии 8 класса является важной частью курса геометрии. Это помогает учащимся развивать навыки анализа и решения геометрических задач, а также применять полученные знания в реальной жизни.

Содержание

Что такое геометрия?

Существуют два основных направления геометрии: планиметрия и стереометрия.

Планиметрия

Планиметрия изучает фигуры и объекты в двухмерном пространстве — плоскости. Она включает в себя изучение таких понятий, как прямая, отрезок, угол, треугольник, четырехугольник, окружность и многое другое. Планиметрия занимается измерением и вычислением периметра, площади и других свойств фигур на плоскости.

Стереометрия

Стереометрия изучает фигуры и объекты в трехмерном пространстве. Этот раздел геометрии занимается изучением таких понятий, как объем, площадь поверхности, пространственные углы, параллельность и перпендикулярность. Стереометрия помогает нам понять форму и размеры трехмерных объектов, таких как куб, цилиндр, конус, пирамида и шар.

Для более удобного и точного изучения геометрических фигур и их свойств используется система аксиом и теорем, основы которых легли в древности и были разработаны такими великими учеными, как Евклид и Архимед.

Планиметрия	Стереометрия
Изучает фигуры в двумерном пространстве (плоскости)	Изучает фигуры в трехмерном пространстве
Основные фигуры: прямая, треугольник, четырехугольник, окружность и т.д.	Основные фигуры: куб, цилиндр, конус, пирамида, шар и т.д.
Свойства: периметр, площадь	Свойства: объем, площадь поверхности

Виды геометрии

В геометрии существует несколько видов геометрии, каждая из которых изучает определенные понятия и свойства пространства и фигур. Рассмотрим некоторые из них:

1. Евклидова геометрия

Евклидова геометрия основана на аксиомах Евклида и изучает плоские и пространственные фигуры, свойства линий, углов, площадей и объемов. Здесь применяются прямые, окружности, треугольники, квадраты и другие известные геометрические фигуры. Евклидова геометрия используется в повседневной жизни и является одной из основных разделов математики.

2. Аналитическая геометрия

Аналитическая геометрия изучает геометрические фигуры с помощью алгебраических методов и координат. Здесь применяются оси координат, уравнения прямых, окружностей, парабол и других кривых. Аналитическая геометрия позволяет более точно и удобно описывать фигуры и решать геометрические задачи с использованием алгебраических методов.

3. Неевклидова геометрия

Неевклидова геометрия изучает геометрические пространства, в которых не выполняются все аксиомы Евклида. В неевклидовой геометрии существуют различные модели пространств с необычными свойствами, например, гиперболическая и эллиптическая геометрия.

Кроме этих основных видов геометрии, существуют также специальные разделы геометрии, изучающие определенные классы фигур или особенности пространства, например, проективная геометрия, дифференциальная геометрия, коническая геометрия и другие.

Изучение геометрии помогает развивать пространственное мышление, а также находит применение в различных науках и практических областях, таких как архитектура, инженерия, физика и компьютерная графика.

Ломаная геометрия: определение и свойства

Ломаная может иметь различную форму: она может быть замкнутой, когда последняя точка соединяется с первой, или разомкнутой. В разомкнутой ломаной первая и последняя точки не соединены.

Свойства ломаной геометрии:

1. Длина ломаной. Длина ломаной равна сумме длин всех ее звеньев. Длину отдельного звена можно найти по формуле, используя координаты точек, которые он соединяет.

2. Стороны и углы. Ломаная разбивает плоскость на фигуры, ограниченные ее звеньями. Внутри каждой фигуры можно выделить стороны и углы.

3. Периметр. Периметр ломаной представляет собой сумму длин всех ее звеньев. Этот параметр полезен при определении длины ограниченной ломаной фигуры.

4. Свойства звеньев. Звенья ломаной не обязательно должны быть прямыми отрезками. Они могут быть кривыми и иметь различную форму, включая дуги окружностей или ломаные линии.

Ломаная геометрия широко применяется в различных областях: строительстве, машиностроении, компьютерной графике и т.д. Понимание ее свойств и особенностей поможет лучше понять пространственные отношения и выполнить точные измерения.

Ознакомившись с определением и свойствами ломаной геометрии, вы сможете более глубоко изучить эту тему и применить полученные знания на практике.

Фигуры в ломаной геометрии

Для ломаной геометрии характерны основные фигуры, которые могут быть использованы в ее построении. Вот несколько часто встречающихся фигур:

Отрезок – самая простая фигура в ломаной геометрии. Он состоит из двух конечных точек, соединенных прямой линией.
Угол – образуется при пересечении двух отрезков. Он имеет вершину и две стороны.
Треугольник – фигура с тремя сторонами и тремя углами. Он может быть использован для построения сложных ломаных фигур.
Прямоугольник – фигура с четырьмя углами, у которых противоположные стороны параллельны.
Пятиугольник – фигура с пятью сторонами и пятью углами.

Это лишь некоторые из фигур, которые могут быть использованы в ломаной геометрии. С помощью этих фигур можно строить более сложные ломаные, состоящие из множества отрезков и углов.

Ломаная геометрия представляет собой важное направление в изучении геометрии, которое находит применение в различных областях, таких как архитектура, дизайн, компьютерная графика и многое другое.

Треугольник

Треугольники классифицируются по длинам и углам своих сторон:

Равнобедренные треугольники: две стороны треугольника равны друг другу. У таких треугольников два равных угла.
Равносторонние треугольники: все три стороны треугольника равны друг другу. У таких треугольников три равных угла, каждый из которых равен 60 градусам.
Прямоугольные треугольники: один из углов треугольника равен 90 градусам, а две другие стороны перпендикулярны друг другу. Одна из сторон треугольника называется гипотенузой, а две другие стороны — катетами.

Треугольники играют важную роль в геометрии и имеют множество свойств и теорем. Изучение треугольников позволяет проводить различные доказательства и решать геометрические задачи. Они также широко применяются в практических областях, таких как строительство, архитектура и дизайн.

Прямоугольник

В прямоугольнике все углы равны 90 градусам, поэтому его стороны являются перпендикулярными. Это делает прямоугольник идеальной фигурой для создания прямых углов и равных сторон.

Прямоугольники широко применяются во многих областях, включая математику, инженерию, архитектуру и строительство. Они являются основой для создания параллелограммов, трапеций и ромбов.

Свойства прямоугольника:

Четыре прямых угла: Каждый угол прямоугольника равен 90 градусам, что делает его прямоугольником.
Равные противоположные стороны: Противоположные стороны прямоугольника имеют одинаковую длину.
Противоположные стороны параллельны: Две противоположные стороны прямоугольника всегда параллельны друг другу.
Диагонали равны: Диагонали прямоугольника имеют одинаковую длину и делят его на два равных треугольника.

Прямоугольник является важной фигурой в геометрии и имеет множество применений в реальном мире.

Параллелограмм

Основные характеристики параллелограмма:

Сторона	Линия, образующая параллелограмм
Угол	Угол между двумя противоположными сторонами
Диагональ	Отрезок, соединяющий две непараллельные вершины параллелограмма

Параллелограмм имеет несколько свойств, которые можно использовать при его изучении:

Противоположные стороны параллельны и равны
Противоположные углы равны
Сумма углов параллелограмма равна 360 градусов
Диагонали параллелограмма делятся пополам

Изучение параллелограмма важно для понимания геометрических принципов и построения сложных фигур. Например, многие другие фигуры, такие как прямоугольник или ромб, являются частными случаями параллелограмма.

Трапеция

Трапеция имеет следующие элементы:

Основания – это параллельные стороны трапеции, которые определяют ее размер и форму. Основание, которое является большей стороной, называется большим основанием, а основание, которое является меньшей стороной, называется малым основанием.
Боковые стороны – это непараллельные стороны трапеции, которые соединяют соответствующие концы оснований. Они могут быть разной длины.
Углы – трапеция имеет два прямых угла, которые находятся на противоположных сторонах трапеции. Остальные два угла трапеции могут быть острыми, тупыми или прямыми.
Высота – это перпендикуляр, опущенный из одного основания на другое основание. Высота трапеции является самым коротким длинным отрезком между двумя параллельными сторонами.
Средняя линия – это отрезок, который соединяет средние точки боковых сторон трапеции. Средняя линия является параллельной основаниям и равна полусумме их длин.

Трапеции часто встречаются в повседневной жизни, например, в форме крыши дома или таблички на дороге. Они также широко используются в геометрии для решения задач и анализа различных фигур.

Важно отметить, что трапеция является одной из множества ломаных геометрических фигур, которые могут быть представлены последовательным соединением отрезков. Ломаная геометрия включает в себя фигуры с разными формами и количеством сторон, такие как треугольники, прямоугольники и многоугольники.

Примеры использования ломаной геометрии

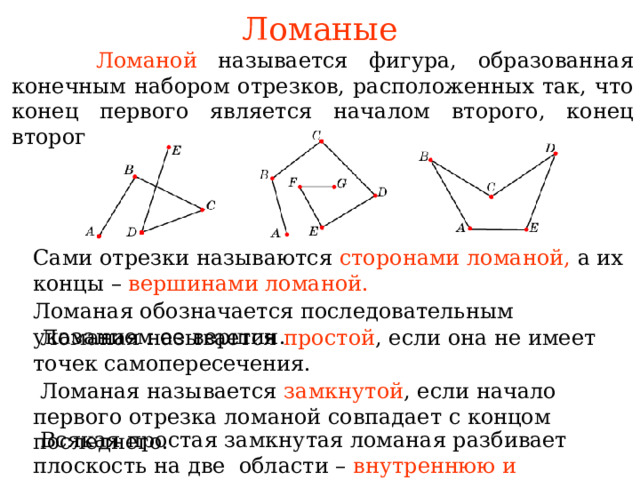
Ломаная геометрия находит свое применение в различных областях. Вот несколько примеров:

1. Карты и планы

Ломаная геометрия широко используется при создании карт и планов. Она позволяет точно передать форму и контур объектов на рисунке. Так, например, ломаная может использоваться для отображения улиц и дорог. Криволинейные части трасс могут быть разбиты на множество отрезков ломаных линий, что позволяет приближенно воссоздать реальные маршруты.

2. Графики функций

Ломаная геометрия также активно применяется при построении графиков функций. Она позволяет визуализировать зависимость одной переменной от другой. Например, график линейной функции представляет собой ломаную линию, соединяющую точки с координатами (x, y), где x и y — значения переменных.

3. Программирование

Ломаная геометрия имеет также практическое применение в программировании. Она может быть использована для построения графических элементов интерфейса, таких как линии, полилинии, границы объектов и многое другое. Такие элементы могут быть созданы с помощью отрезков ломаных линий, что дает возможность рисовать сложные формы и очертания.

4. Обработка изображений

В области обработки изображений ломаная геометрия применяется для выделения контуров объектов. Алгоритмы, основанные на ломаных линиях, позволяют определить границы между объектами на изображении. Такой подход может использоваться, например, при распознавании лиц на фотографиях или для автоматического выделения объектов на изображении.

Таким образом, ломаная геометрия является важным инструментом для представления и визуализации различных объектов и зависимостей в геометрии, науке и технике.

Вопрос-ответ:

Что такое ломаная в геометрии?

Ломаная — это геометрическая фигура, состоящая из отрезков, соединяющих точки на плоскости. Она может быть и замкнутой, и незамкнутой.

Как называются точки, соединенные отрезками в ломаной?

Точки, соединенные отрезками в ломаной, называются вершинами ломаной.

Какие свойства имеет ломаная?

У ломаной есть несколько свойств. Например, сумма всех углов при вершинах ломаной равна 180 градусов. Также, если все отрезки ломаной равны друг другу, то она называется равнобочной.