
Графы являются одной из основных структур данных в теории графов и находят широкое применение в различных областях, начиная от компьютерной науки и математики и заканчивая социологией и транспортными системами. Графы могут быть ориентированными и неориентированными, причем в данной статье мы рассмотрим неориентированные графы.
Неориентированный граф представляет собой совокупность вершин и ребер, где ребра не имеют направления. В таком графе каждое ребро представляет собой связь между двумя вершинами и может быть представлено как неупорядоченная пара вершин. При этом, отношение «смежности» между двумя вершинами в неориентированном графе является симметричным, то есть если вершина A связана с вершиной B, то и вершина B связана с вершиной A.
Примером неориентированного графа может служить граф дружеских связей среди группы людей. Каждая вершина графа может представлять конкретного человека, а ребро — дружескую связь между двумя людьми. В таком графе, отношение «дружбы» является взаимным и не имеет направления.
Неориентированный граф: что это такое?
Неориентированный граф полезен для моделирования различных ситуаций, где связи между объектами не имеют строго установленного направления. Такой граф может быть использован, например, для представления социальных сетей, дорожных сетей, системы связей между компьютерами и других объектов, где взаимодействие происходит в обоих направлениях.
Основные понятия
Для работы с неориентированным графом существуют несколько основных понятий:
- Вершина — это один из элементов графа. Вершины могут представлять собой объекты, точки на карте или другие абстрактные понятия.
- Ребро — это связь между двумя вершинами. Ребра могут иметь различные свойства, такие как вес, цвет или пропускная способность.
- Степень вершины — это количество ребер, связанных с данной вершиной.
Примеры неориентированных графов
Существует множество примеров неориентированных графов:
- Граф дружеских связей — вершинами являются люди, а ребра представляют собой дружбу между ними.
- Граф дорожной сети — вершинами являются перекрестки или города, а ребра представляют собой дороги между ними.
- Граф компьютерной сети — вершинами являются компьютеры или узлы, а ребра представляют собой сетевые связи.
Неориентированный граф играет важную роль в теории графов и имеет много применений в реальном мире. Изучение его основных понятий и свойств позволяет анализировать и решать различные задачи, связанные с моделированием и оптимизацией сложных систем.
Основные понятия и определения
В неориентированном графе узлы (вершины) представляют отдельные объекты, а ребра — связи между ними. Каждое ребро может быть представлено в виде упорядоченной пары вершин, которые оно соединяет.
Множество всех вершин в графе называется вершинным множеством, обозначается V.
Множество всех ребер в графе называется реберным множеством, обозначается E.
Степенью вершины графа называется число ребер, оканчивающихся в этой вершине. Простейшим примером степени вершины может быть количество смежных с ней ребер.
Путь в графе — это последовательность ребер, соединяющих вершины. Если все вершины разные, путь называется простым.
Цикл в графе — это путь, в котором первая и последняя вершины совпадают.
Связный граф, или компонента связности, — это максимальный подграф, в котором есть путь между любыми двумя вершинами.
Изолированная вершина — это вершина, не соединенная ни с одним ребром.
Петля — это ребро, соединяющее вершину с самой собой.
Двудольный граф — это граф, вершины которого можно разбить на две непересекающиеся части таким образом, что все его ребра соединяют вершины разных частей.
Полный граф — это граф, в котором каждая пара различных вершин соединена ребром.
Это основные понятия и определения, необходимые для понимания неориентированных графов.
Примеры неориентированных графов
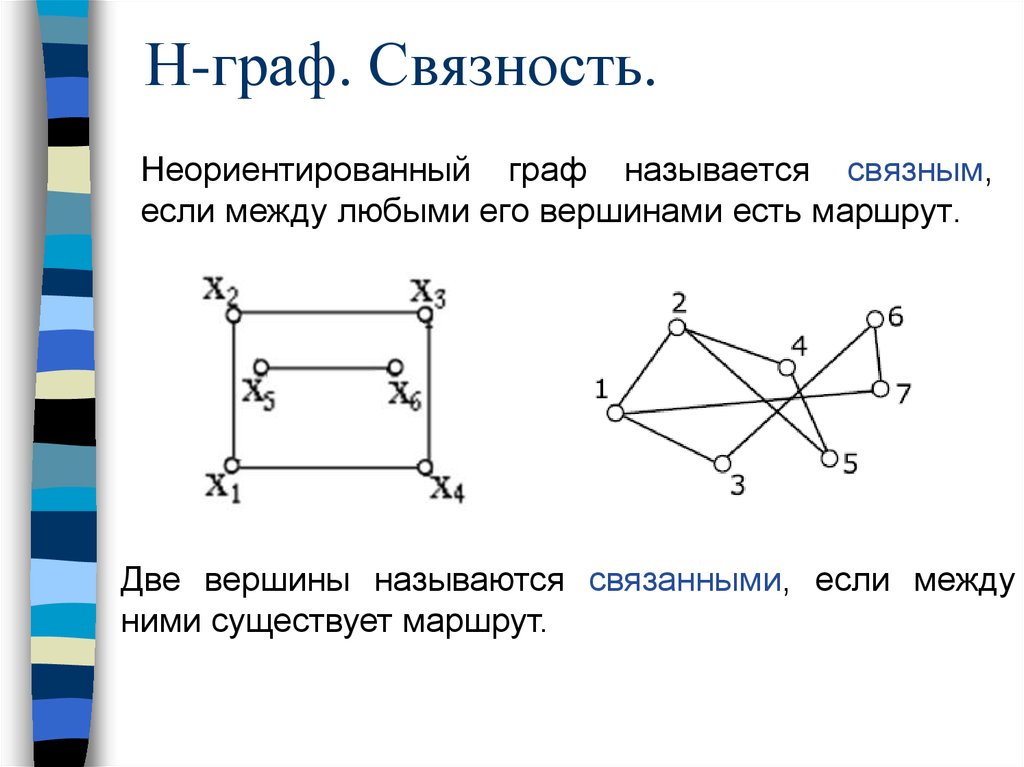
Граф дружбы в социальных сетях
В социальных сетях, таких как Facebook или ВКонтакте, каждый участник представляется вершиной, а дружеские связи между ними — ребрами. При этом связь между двумя людьми является взаимной и не имеет направления. Такой граф можно представить в виде неориентированного графа. Он может использоваться для анализа структуры социальной сети, поиска сообществ и др.
Транспортные сети
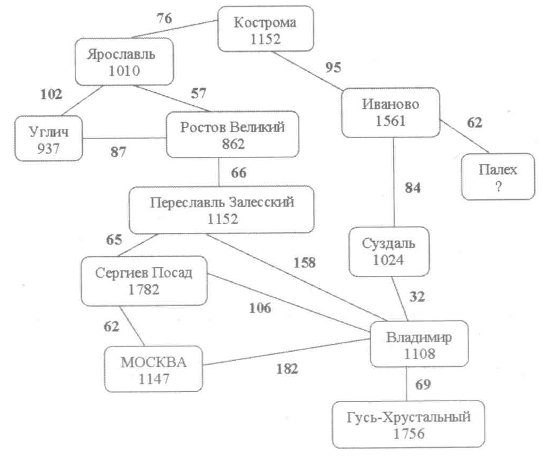
Еще одним примером неориентированного графа является транспортная сеть. В этом случае вершины представляют города или локации, а ребра — дороги или другие виды транспорта, связывающие их. Транспортная связь между двумя городами не зависит от направления движения. Такой граф можно использовать для оптимизации маршрутов и планирования логистических систем.
Примеры неориентированных графов не ограничиваются этими двумя областями. Они могут быть использованы для моделирования множества различных ситуаций, в которых направление ребра не имеет значения.
Пути и циклы в неориентированных графах
Путь в графе — это последовательность вершин, в которой каждая вершина соединена ребром с последующей вершиной в последовательности. Путь может быть направленным от одной вершины к другой или обратно.
Цикл — это путь, включающий начальную и конечную вершины, и имеющий длину больше одного. В неориентированном графе цикл может быть замкнутым и не иметь дублирующих вершин и ребер. Цикл может быть также простым, то есть не иметь повторяющихся вершин кроме начальной и конечной вершины.
Если в графе существует путь между любыми двумя вершинами, то такой граф называется связным. Если же не существует пути между какими-то вершинами, то граф называется несвязным.
Пути и циклы в неориентированных графах играют важную роль в различных областях, таких как транспортная логистика, социальные сети, анализ данных и другие. Изучение свойств и алгоритмов для поиска путей и циклов в неориентированных графах позволяет решать множество задач, связанных с оптимизацией и анализом таких систем.
Сведение ориентированного графа к неориентированному
Для сведения ориентированного графа к неориентированному ребра, направленные в разных направлениях, объединяются в одно неориентированное ребро.
Пример:
Рассмотрим ориентированный граф с вершинами A, B, C и ребрами (A, B), (B, C) и (C, A). Для приведения данного графа к неориентированному, ребра (A, B) и (B, C) объединяются в неориентированное ребро AB, а ребра (C, A) и (B, C) объединяются в неориентированное ребро CA.
Полученный неориентированный граф будет иметь вершины A, B и C, а ребра AB, BC и CA будут неориентированными.
В результате сведения ориентированного графа к неориентированному, мы получаем граф, в котором все ребра не имеют направления. Такой граф называется неориентированным графом.
Применение неориентированных графов в реальной жизни
Социальные сети
Неориентированные графы могут помочь в анализе социальных сетей, таких как Facebook или Twitter. Каждый участник сети представляется как вершина графа, а отношения между участниками — как ребра. Неориентированные графы позволяют анализировать такие важные параметры, как влиятельность, связность и группы друзей.
Транспортные сети
Неориентированные графы находят применение и в области транспортных сетей. Вершины соответствуют пересечениям дорог или остановкам, а ребра — сами дороги или автобусные маршруты. Анализ таких графов помогает оптимизировать планирование маршрутов, снижая транспортные заторы и время в пути.
| Примеры | Описание |
|---|---|
| Граф дорог | Моделирование дорожной сети города, что позволяет анализировать дорожные условия, планировать новые дорожные проекты и оптимизировать движение |
| Граф метро | Изучение маршрутов и подключений в системе метро или железной дороге для максимальной эффективности и удобства пассажиров |
| Граф авиа-маршрутов | Анализ действующих авиалиний, планирование новых маршрутов и определение оптимальных пересадочных точек |
Применение неориентированных графов в транспортных системах помогает создать более эффективные и удобные пути передвижения для людей и грузов.
Таким образом, неориентированные графы играют важную роль в разных областях реальной жизни, позволяя анализировать сложные системы и принимать более информированные решения.
Алгоритмы обработки неориентированных графов
Обработка неориентированных графов имеет важное значение в различных областях, таких как компьютерная графика, социальные сети, транспортные системы и многие другие. У них есть множество применений, начиная от нахождения кратчайшего пути между точками до определения связности в сетях или поиска оптимальных маршрутов.
Алгоритмы поиска пути в неориентированном графе:
- Алгоритм поиска в ширину (BFS) — позволяет найти кратчайший путь между двумя вершинами в графе. Он основывается на принципе обхода «в ширину» от стартовой вершины, постепенно расширяяся к соседним вершинам.
- Алгоритм поиска в глубину (DFS) — позволяет найти путь между двумя вершинами, перебирая все возможные пути от стартовой вершины до целевой. Он основывается на принципе обхода «в глубину» и использует стек для отслеживания пройденных вершин.
Алгоритмы нахождения связной компоненты:
- Алгоритм обхода в глубину (DFS) — позволяет определить, является ли граф связным. Он основывается на принципе обхода вершин и отмечает посещенные вершины, чтобы определить, есть ли путь от одной вершины к другой.
- Алгоритм поиска компонент связности — позволяет найти все связные компоненты в графе. Он основывается на запуске алгоритма обхода в глубину или обхода в ширину из каждой вершины, и помечает пройденные вершины для определения компонент связности.
Это лишь несколько примеров алгоритмов обработки неориентированных графов. В зависимости от задачи, могут использоваться и другие алгоритмы, такие как алгоритмы поиска минимального остовного дерева, нахождения циклов и т. д. Важно выбрать наиболее подходящий алгоритм для конкретной задачи, чтобы эффективно обработать неориентированный граф.
Вопрос-ответ:
Какой граф называется неориентированным?
Неориентированный граф — это граф, в котором отсутствуют направленные ребра. То есть, любая пара вершин соединяется неориентированным ребром, которое можно рассматривать как двунаправленное.
Как отличить ориентированный граф от неориентированного?
Ориентированный граф имеет направленные ребра, в то время как неориентированный граф имеет неориентированные ребра, которые можно рассматривать как двунаправленные. В ориентированном графе можно перемещаться только в направлении от одной вершины к другой, в то время как в неориентированном графе перемещение возможно в обоих направлениях.
Какие примеры неориентированных графов существуют?
Примерами неориентированных графов могут служить: граф, моделирующий дорожную сеть, где каждая вершина представляет собой перекресток или узел, а ребра — дороги; граф, моделирующий социальные связи, где вершины представляют собой людей, а ребра — отношения между ними; граф, моделирующий систему компьютерных сетей, где вершины представляют собой компьютеры, а ребра — соединения между ними.
В чем отличие между простым и несвязным графом?
Простой граф — это граф, в котором нет петель (ребер, соединяющих вершину с самой собой) и кратных ребер (нескольких ребер, соединяющих одну и ту же пару вершин). Несвязный граф — это граф, в котором есть несвязанные между собой компоненты, то есть некоторые вершины не могут быть достигнуты от других вершин.
Какие сложные алгоритмы могут использоваться для работы с неориентированными графами?
Для работы с неориентированными графами могут применяться такие алгоритмы, как обход в ширину (BFS), обход в глубину (DFS), алгоритм Дейкстры для поиска кратчайших путей, алгоритм Прима и алгоритм Крускала для построения минимального остовного дерева, алгоритм Хопкрофта-Карпа для поиска максимального паросочетания и другие.