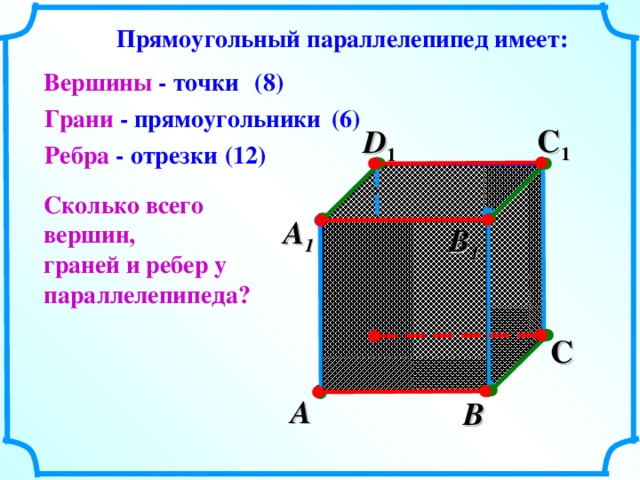
Параллелепипед – это геометрическое тело в трехмерном пространстве, которое обладает определенными свойствами и характеристиками. Это особый тип прямоугольного параллелепипеда, у которого все грани прямоугольные и параллельные друг другу. Такая фигура является одной из основных форм в геометрии и широко применяется в различных областях.
Основные характеристики параллелепипеда – прямые углы и равные противоположные грани. Его грани представляют собой прямоугольники, а все ребра параллельны между собой. Фигура может быть вытянутой вдоль одного из ребер или иметь более компактные симметричные пропорции.
Параллелепипеды широко используются в архитектуре, строительстве, геометрии, физике, геодезии и других областях. Они являются одной из базовых форм, на основе которой создаются различные конструкции и объекты. В архитектуре параллелепипеды часто встречаются в виде зданий и сооружений, в геометрии и физике использование параллелепипедов позволяет решать сложные задачи и проводить точные расчеты.
Определение параллелепипеда
1. Плоские грани
Параллелепипед имеет шесть плоских граней, каждая из которых является прямоугольником. Грани параллелепипеда расположены параллельно друг другу и имеют одинаковые формы и размеры.
2. Ребра и вершины
У параллелепипеда есть 12 ребер, каждое из которых соединяет две смежные вершины. Всего у параллелепипеда восемь вершин, каждая из которых соединена тремя ребрами.
3. Параллельные противоположные грани

Противоположные грани параллелепипеда расположены параллельно друг другу. Это позволяет параллелепипеду обладать особыми свойствами, такими как равномерное распределение сил и одинаковая интенсивность освещения на всех его гранях.
Параллелепипед является одним из основных пространственных геометрических тел и широко применяется в инженерии, строительстве и геометрии. Он может быть различной формы и размеров, но всегда сохраняет свои основные характеристики.
Геометрическая форма

Определение
Параллелепипед — это трехмерный объект, который образован соединением трех параллельных прямоугольных граней. Три попарно перпендикулярных ребра называются ребрами основания, а три попарно перпендикулярных ребра, соединяющие соответствующие вершины этих ребер, называются боковыми ребрами. Все шесть граней параллелепипеда являются прямоугольниками.
Свойства
Параллелепипед обладает рядом свойств:
- У него шесть граней, две из которых всегда параллельны друг другу.
- У каждой грани два параллельных ребра и два перпендикулярных ребра.
- У него 12 ребер и 8 вершин.
- У него равноприметной основание.
- Объем параллелепипеда рассчитывается по формуле V = a * b * c, где a, b и c — длины его трех ребер.
- Площадь поверхности параллелепипеда рассчитывается по формуле S = 2(ab + ac + bc), где a, b и c — длины его трех ребер.
Основные элементы параллелепипеда
Основные элементы параллелепипеда включают:
1. Боковые грани: Параллельные грани параллелепипеда, которые имеют одинаковую форму и размеры.
2. Вершины: Угловые точки параллелепипеда, где пересекаются его ребра.
3. Рёбра: Отрезки прямых линий, которые соединяют вершины параллелепипеда. У параллелепипеда есть 12 ребер, при этом каждое ребро соединяет две вершины.
4. Диагонали: Отрезки прямых линий, которые соединяют противоположные вершины или грани параллелепипеда. Параллелепипед имеет три пары диагоналей, которые проходят через его центр.
5. Высоты: Отрезки прямых линий, которые соединяют вершину параллелепипеда с противоположной гранью. Высоты могут проходить через центр грани или быть наклонными.
Все эти элементы являются важными характеристиками параллелепипеда, позволяющими определить его форму и свойства.
Стороны и углы
У параллелепипеда также есть 12 ребер — это отрезки, соединяющие вершины параллелепипеда. Каждое ребро образуется пересечением двух плоскостей, соединяющих соседние вершины.
Углы
Параллелепипед имеет 8 вершин. На каждой вершине сходятся три ребра и три плоскости. Угол между двумя ребрами, исходящими из одной вершины, называется вершинным углом. Всего в параллелепипеде 8 вершинных углов.
Также у параллелепипеда есть 6 граней — это плоскости, которые образуют параллелограммы. Каждая грань образуется соединением по три вершины.
Важно отметить, что все углы в параллелепипеде прямые, то есть равны 90 градусам.
Объем и площадь параллелепипеда
Объем параллелепипеда
Объем параллелепипеда — это количество пространства, занимаемого этим телом. Для расчета объема параллелепипеда необходимо умножить длину одной из его сторон (a), на ширину другой стороны (b), на высоту (h). Математически это можно записать формулой:
Объем = a * b * h
Площадь параллелепипеда
Площадь параллелепипеда — это сумма площадей его граней. Для расчета площади необходимо найти площадь каждой грани и сложить их. Общая формула для расчета площади параллелепипеда:
Площадь = 2 * (a * b + a * h + b * h)
Где a, b и h — длины сторон параллелепипеда.
Виды параллелепипедов
Прямоугольный параллелепипед — это параллелепипед, у которого все углы прямые.
Квадратный параллелепипед — это параллелепипед, у которого все грани равны квадратам.
Куб — это параллелепипед, у которого все грани равны квадратам и все ребра равны.
Несимметричный параллелепипед — это параллелепипед, у которого все грани являются параллелограммами, но его ребра не равны друг другу.
В зависимости от своей формы и размеров параллелепипеды могут использоваться в различных областях, например, в строительстве, геометрии, физике и других.
Сферы применения параллелепипеда
- Архитектура и строительство: Параллелепипеды широко используются в проектировании и строительстве различных сооружений. Они могут быть использованы как основные структурные элементы зданий, например, в стенах и фундаментах. Кроме того, параллелепипеды могут использоваться в создании оконных и дверных проемов.
- Упаковка и хранение: Параллелепипеды часто используются в упаковке товаров и контейнерах для хранения. Их прямоугольная форма и ровные грани делают их легкими в использовании и стабильными в стопках или рядами.
- Транспорт и логистика: Параллелепипеды используются в транспортных средствах и логистических системах для упаковки и перевозки грузов. Они позволяют оптимизировать использование пространства внутри транспортных средств и упрощают погрузочно-разгрузочные операции.
- Мебельное производство: Параллелепипеды используются в мебельном производстве как основные элементы для создания различных предметов мебели, например, столов, стульев, шкафов и полок.
- Инженерные расчеты: Параллелепипеды используются в инженерных расчетах и моделировании для представления объектов или сред в трехмерном пространстве. Они могут быть использованы для моделирования зданий, оборудования, геологических структур и многого другого.
Это лишь некоторые из множества сфер применения параллелепипеда. Благодаря своим уникальным особенностям и простой форме, параллелепипед остается важным элементом в различных областях науки, техники и искусства.
Вопрос-ответ:
Что такое параллелепипед?
Параллелепипед — это геометрическое тело, у которого все грани являются параллелограммами. У него прямоугольный параллелограмм — основание, и все его боковые грани также являются прямоугольными параллелограммами.
Какая формула позволяет найти объем параллелепипеда?
Для нахождения объема параллелепипеда нужно перемножить длину, ширину и высоту этого тела. Таким образом, формула для нахождения объема параллелепипеда имеет вид: V = a * b * h, где a — длина, b — ширина, h — высота параллелепипеда.
В чем отличие параллелепипеда от куба?
Главное отличие параллелепипеда от куба заключается в том, что у параллелепипеда все ребра имеют разные длины. В то же время, у куба все его ребра одинаковой длины. Куб является особым случаем параллелепипеда, у которого все ребра равны друг другу и все грани параллельные.
Какие свойства имеет параллелепипед?
У параллелепипеда есть несколько характеристик и свойств. Например, его противоположные грани равны и параллельны друг другу, он имеет шесть граней и восемь вершин. Также у параллелепипеда есть три пары параллельных ребер и шесть граней, каждая из которых перпендикулярна двум другим.
Какие примеры можно привести параллелепипедов в реальной жизни?
Параллелепипеды можно встретить в разных сферах жизни. Например, кирпичи, коробки, книги и тетради имеют форму параллелепипеда. Также в некоторых зданиях можно найти комнаты, которые имеют прямоугольную форму с параллельными стенами, а значит, являются параллелепипедами.