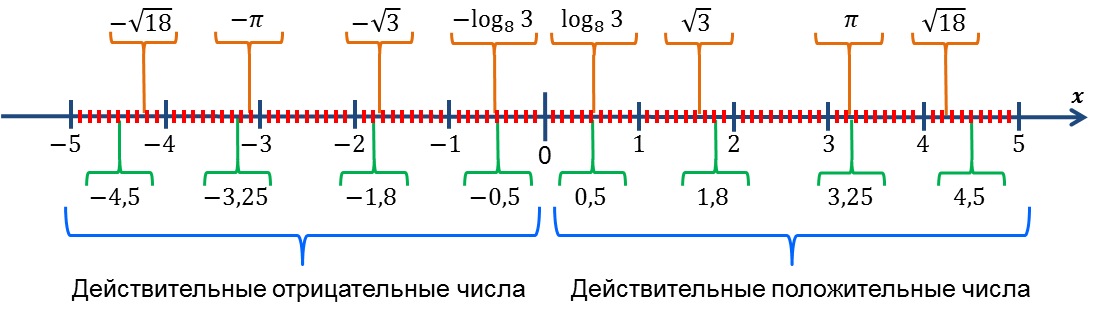
Положительные числа — это числа, которые больше нуля и отличаются от отрицательных чисел. Они имеют важное значение в математике и используются в различных областях жизни.
Одно из основных свойств положительных чисел — они используются для измерения и сравнения. Например, если у вас есть два положительных числа, вы можете сравнить их и определить, какое из них больше или меньше.
Положительные числа также обладают свойством увеличения. Если добавить к положительному числу другое положительное число, результат будет еще больше. Например, если сложить 3 и 5, получится 8, что больше, чем каждое из входных чисел.
Примеры положительных чисел включают такие числа, как 1, 7, 12, 100 и т. д. Они широко используются в нашей повседневной жизни, например, для подсчета денег, измерения времени или оценки успехов в спорте.
Определение положительных чисел
Примеры положительных чисел: 1, 5, 10, 100, 1000.
Что такое положительные числа
Положительные числа играют важную роль в математике и ежедневной жизни. Они используются для измерения массы, длины, времени, температуры и других физических величин. Например, масса тела, равная 2 килограммам, является положительным числом, так как она больше нуля.
| Примеры положительных чисел |
|---|
| 5 |
| 10 |
| 25 |
| 0.75 |
| 3/4 |
Все эти числа являются положительными, так как они больше нуля.
Положительные числа имеют множество свойств и правил, которые позволяют выполнять различные операции с ними, такие как сложение, вычитание, умножение и деление. Знание и понимание положительных чисел играет важную роль в развитии математических навыков и решении задач из разных областей.
Диапазоны положительных чисел
Диапазон положительных целых чисел включает все целые числа, которые больше нуля. Например: 1, 2, 3, 4…
Диапазон положительных десятичных чисел включает все числа, которые больше нуля, но меньше единицы. Например: 0.1, 0.2, 0.3, 0.4…
Диапазон положительных рациональных чисел включает все десятичные числа больше нуля, но меньше бесконечности. Например: 0.2, 0.5, 0.8…
Диапазон положительных иррациональных чисел включает все числа, которые не могут быть представлены десятичной дробью и больше нуля. Например: √2, π, e…
Диапазон положительных дробных чисел включает все числа, которые можно представить десятичной дробью больше нуля. Например: 0.1, 0.25, 0.5…
Диапазон положительных действительных чисел включает все числа, которые могут быть представлены дробью или десятичной дробью и больше нуля. Например: 1, 1.5, 2, 2.7…
Диапазон положительных чисел может быть бесконечным, так как чисел больше нуля бесконечное количество.
Запомните: положительные числа — это числа, которые больше нуля, и они могут включать различные диапазоны, в зависимости от их характеристик.
Свойства положительных чисел
1. Возрастание: Положительные числа увеличиваются по значению, то есть каждое следующее число больше предыдущего. Например, 1, 2, 3, 4, 5 и т.д.
2. Сложение: Положительные числа можно складывать между собой. Результатом сложения двух положительных чисел всегда будет положительное число. Например, 2 + 3 = 5.
3. Умножение: Положительные числа можно умножать между собой. Результатом умножения двух положительных чисел всегда будет положительное число. Например, 2 * 3 = 6.
4. Деление: Положительные числа можно делить между собой. Результатом деления положительного числа на положительное число всегда будет положительное число. Например, 6 / 2 = 3.
5. Свойство неравенства: Если два положительных числа сравниваются, то большее число всегда больше меньшего числа. Например, 5 > 3.
6. Свойство противоположности: Каждое положительное число имеет свое противоположное отрицательное число. Например, противоположное число для 3 является -3.
7. Возведение в степень: Положительные числа можно возводить в степень. Результатом возведения положительного числа в положительную степень всегда будет положительное число. Например, 2^3 = 8.
8. Извлечение корня: Положительные числа можно извлекать корень. Результатом извлечения корня из положительного числа всегда будет положительное число. Например, √9 = 3.
9. Предел: Положительные числа не имеют верхнего предела, то есть их значения могут быть бесконечно большими. Например, число 10^1000 является положительным числом.
10. Иррациональность: Некоторые положительные числа являются иррациональными, то есть их значение не может быть представлено в виде десятичной дроби. Например, число π (пи).
Умножение положительных чисел
Умножение положительных чисел можно представить как повторение сложения. Например, если умножить число 3 на 2, это означает, что мы складываем число 3 два раза: 3 + 3. В результате получаем число 6, которое больше нуля и, следовательно, является положительным числом.
Примеры умножения положительных чисел:
- 2 * 2 = 4: умножение числа 2 на само себя дает произведение 4.
- 4 * 3 = 12: умножение числа 4 на 3 дает произведение 12.
- 5 * 6 = 30: умножение числа 5 на 6 дает произведение 30.
Таким образом, при умножении двух положительных чисел мы всегда получаем положительное число в качестве результата.
Сложение положительных чисел
Примеры сложения положительных чисел:
- 2 + 3 = 5
- 7 + 9 = 16
- 12 + 6 = 18
Когда мы складываем положительные числа, мы объединяем их вместе, чтобы получить общую сумму. Например, если у нас есть 2 яблока и мы добавляем к ним ещё 3 яблока, мы получим 5 яблок в общей сложности.
Сложение положительных чисел можно представить и в виде числовой оси. Если мы имеем начальную точку на числовой оси и прибавляем положительное число, мы перемещаемся вправо по оси.
Сложение положительных чисел является коммутативной операцией, что означает, что порядок слагаемых не имеет значения. Например, 2 + 3 будет равно 3 + 2.
Операция сложения положительных чисел позволяет нам объединять и складывать количество или величину чего-либо. Она широко используется в повседневной жизни, например, при подсчёте суммы покупок или расчёте финансовых величин.
Сравнение положительных чисел
Сравнение положительных чисел можно производить с помощью специальных знаков: «больше» (>) и «меньше» (<). Если число А больше числа В, то говорят, что А > В. Если число А меньше числа В, то говорят, что А < В.
Примеры сравнения положительных чисел:
| Число А | Число В | Результат сравнения |
|---|---|---|
| 4 | 2 | 4 > 2 |
| 7 | 9 | 7 < 9 |
| 12 | 12 | 12 = 12 |
В примерах выше видно, что число 4 больше числа 2 (4 > 2), число 7 меньше числа 9 (7 < 9), а число 12 равно числу 12 (12 = 12).
Сравнение положительных чисел очень важно, так как позволяет устанавливать иерархию между ними и применять их в различных математических операциях.
Вопрос-ответ:
Что такое положительные числа?
Положительные числа — это числа, которые больше нуля. Они находятся справа от нуля на числовой прямой.
Какие примеры положительных чисел можно привести?
Примеры положительных чисел: 1, 2, 3, 4, 5 и так далее. Все числа больше нуля являются положительными.
Какое свойство имеют положительные числа в алгебре?
Одно из свойств положительных чисел в алгебре заключается в том, что их можно складывать и умножать без ограничений. Результатом сложения или умножения положительных чисел также будет положительное число.
Как положительные числа связаны с отрицательными числами?
Положительные числа и отрицательные числа являются противоположными. Отрицательные числа находятся слева от нуля на числовой прямой, в то время как положительные числа — справа от нуля. Отрицательные числа можно представить как дополнение к положительным числам.
Можно ли умножать положительные числа на отрицательные?
Да, положительные числа можно умножать как на положительные, так и на отрицательные числа. Результатом такого умножения будет отрицательное число.
Что такое положительные числа?
Положительные числа — это числа, которые больше нуля. Они обозначаются без знака и используются для представления количества или значения, которыми нельзя измерить отрицательные значения или отсутствие таковых.
Какие особенности имеют положительные числа?
Положительные числа имеют несколько особенностей. Во-первых, они больше нуля и находятся справа от нуля на числовой прямой. Во-вторых, они могут быть складываны, вычитаны, умножены и делены друг на друга. Наконец, положительные числа обладают свойством увеличения при сложении с другими положительными числами.