В мире математики существует множество систем счисления, однако одной из наиболее распространенных и применяемых является система счисления с позиционной нотацией. В этой системе цифры имеют различные количественные эквиваленты в зависимости от их положения в записи числа.
Система счисления с позиционной нотацией основывается на понятии разрядов. Каждый разряд в числе обладает весом, который является степенью основания системы счисления. Например, в десятичной системе счисления вес каждого разряда увеличивается в 10 раз по сравнению с предыдущим разрядом.
Каждая цифра в числе имеет свой вес, исходя из своего положения в записи числа. Например, в числе 9876 вес первой цифры (9) равен 1000, вес второй цифры (8) равен 100, вес третьей цифры (7) равен 10, а вес четвертой цифры (6) равен 1. Таким образом, положение цифры в записи числа определяет ее количественный эквивалент.
Система счисления с позиционной нотацией имеет широкое применение в различных областях, включая информатику, финансы, физику и многие другие. Благодаря этой системе мы можем удобно представлять числа, выполнять арифметические операции и решать различные задачи, связанные с количественными значениями.
Таким образом, система счисления с позиционной нотацией является одной из фундаментальных математических концепций, которая облегчает работу с числами и позволяет нам легко осуществлять различные вычисления и анализ.
Что такое количественный эквивалент цифры в записи числа?
Например, в десятичной системе количественный эквивалент цифры зависит от ее позиции, от единиц до тысяч, миллионов и т.д. Каждая цифра имеет свое значение, умноженное на определенную степень десяти. Например, цифра 7 в числе 578 представляет собой 7 единиц, что эквивалентно 7 * 10^0.
В других системах счисления, таких как двоичная или восьмеричная, значение цифры также зависит от ее положения. Например, в двоичной системе значение цифры может быть либо 0, либо 1, и каждая цифра имеет свою степень двойки.
Количественный эквивалент цифры в записи числа является важным аспектом для правильного понимания чисел и выполнения математических операций. Он помогает определить вес каждой цифры и вычислить общую стоимость числа.
Системы и особенности записи чисел
В позиционной системе счисления каждая цифра имеет свое значение в зависимости от ее положения в числе. Например, в десятичной системе цифра 1 на первом месте имеет значение единицы, аналогично цифра 1 на десятом месте имеет значение десятков. Таким образом, число 365 представляет собой сумму 3*100 + 6*10 + 5*1.
Позиционная система счисления позволяет использовать ограниченное количество символов для записи большого количества чисел. Например, все числа от 0 до 9 могут быть записаны с помощью цифр от 0 до 9. Числа от 10 до 99 записываются с помощью комбинации двух цифр, а числа от 100 до 999 – с помощью комбинации трех цифр.
Одно из преимуществ позиционной системы счисления заключается в ее универсальности. Она позволяет записывать числа любой величины и обеспечивает эффективную работу с ними. Позиционная система также используется в большинстве вычислительных устройств, включая компьютеры и калькуляторы.
Однако, помимо позиционной системы счисления, существуют и другие системы записи чисел, такие как римская система счисления или двоичная система счисления. Каждая из этих систем имеет свои особенности и применяется в определенных областях или для решения конкретных задач.
Важно знать, что системы записи чисел – не только средство математического выражения, но и отображение культурного и исторического развития человечества. Изучение различных систем записи чисел помогает лучше понять историю и культуру нашего мира.
Зависимость эквивалента от положения цифры
Существуют различные системы счисления, в которых количественный эквивалент цифры зависит от ее положения в записи числа. Это означает, что одна и та же цифра, находящаяся в разных разрядах числа, может иметь разную стоимость или вес.
Наиболее распространенной системой счисления, в которой зависимость эквивалента от положения цифры играет важную роль, является десятичная система. В десятичной системе каждая цифра в числе имеет свой вес, который определяется ее положением в числовой записи. Например, в числе 123, цифра 1 имеет вес 100, цифра 2 имеет вес 10, а цифра 3 имеет вес 1.
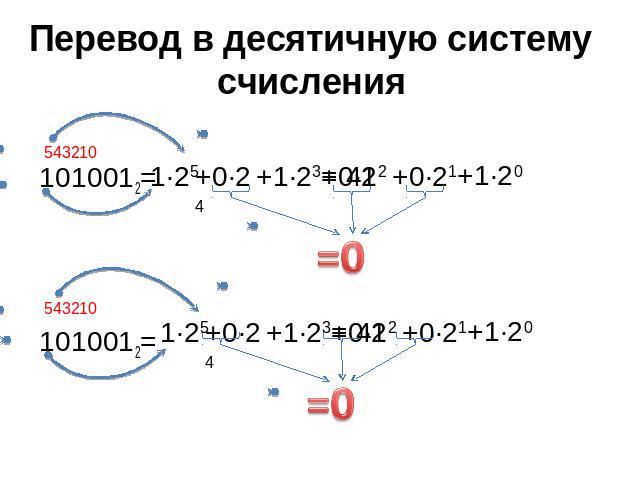
Следующей популярной системой счисления с зависимостью эквивалента от положения цифры является двоичная система. В двоичной системе каждая цифра может быть либо 0, либо 1, и вес каждой цифры также зависит от ее положения в числовой записи. Например, в числе 101, цифра 1 в крайнем правом разряде имеет вес 1, цифра 0 в среднем разряде имеет вес 2, а цифра 1 в крайнем левом разряде имеет вес 4.
Таблица: Зависимость эквивалента от положения цифры в десятичной системе
| Цифра | Положение | Вес |
|---|---|---|
| 1 | Единицы | 1 |
| 2 | Десятки | 10 |
| 3 | Сотни | 100 |
Таблица: Зависимость эквивалента от положения цифры в двоичной системе
| Цифра | Положение | Вес |
|---|---|---|
| 1 | Единицы | 1 |
| 0 | Двоичные десятки | 2 |
| 1 | Двоичные сотни | 4 |
В зависимости от системы счисления, вес каждой цифры может различаться. Это позволяет использовать различные системы счисления в разных областях, в зависимости от конкретных требований и удобства использования.
Десятичная система счисления и эквивалент цифр
Основано она на принципе позиционной записи чисел. Это означает, что в данной системе цифры имеют различный количественный эквивалент в зависимости от их положения в записи числа. Например, цифра 5 в числе 583 будет иметь эквивалент в размере 500, а в числе 356 – эквивалент в размере 50.
Эквивалент цифр в десятичной системе счисления:
| Цифра | Эквивалент |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 4 |
| 5 | 5 |
| 6 | 6 |
| 7 | 7 |
| 8 | 8 |
| 9 | 9 |
Примеры эквивалента цифр:
В числе 347, цифра 3 имеет эквивалент в размере 300, цифра 4 – эквивалент в размере 40, и цифра 7 – эквивалент в размере 7.
Другие системы счисления и их количественные эквиваленты
Существуют различные системы счисления, в которых количественный эквивалент цифры зависит от ее положения в записи числа. Это означает, что одна и та же цифра может иметь различное значение, в зависимости от ее позиции в числе.
Самая распространенная система счисления — десятичная система, или система с основанием 10. В десятичной системе каждая цифра имеет свое значение, зависящее от ее положения в числе. Например, цифра «5», стоящая в позиции единиц, имеет значение «5». Но если эта же цифра «5» стоит в позиции десятков или сотен, то она имеет соответственно значение «50» или «500».
Однако существуют и другие системы счисления, в которых основание отличается от десятичной системы. Например, в двоичной системе счисления основанием является число 2, и только две цифры — «0» и «1» — используются для записи чисел. При этом значение каждой цифры зависит от ее положения в числе: цифра «1» в позиции единиц имеет значение «1», а цифра «1» в позициях двоек или четверок имеет значения «2» или «4», соответственно.
Существуют также системы счисления с другими основаниями, например, восьмеричная (с основанием 
и шестнадцатеричная (с основанием 16). В этих системах счисления каждая цифра имеет свое значение, зависящее от ее положения в числе. Например, восьмеричная система счисления использует цифры от «0» до «7», а шестнадцатеричная система счисления использует цифры от «0» до «9» и буквы от «A» до «F».
Таким образом, системы счисления, в которых количественный эквивалент цифры зависит от ее положения в записи числа, представляют широкий круг математических концепций и инструментов, которые находят применение в различных областях науки и техники.
Разряды и разрядный эквивалент
В числовых системах с позиционным представлением, таких как десятичная система, двоичная система и другие, число представляется в виде последовательности цифр, разделенных на разряды. Эти разряды указывают на положение цифры в числе и определяют ее значимость.
Каждый разряд имеет свою степень. Например, в десятичной системе разряды справа налево имеют следующую степень: единицы (10^0), десятки (10^1), сотни (10^2), тысячи (10^3) и так далее. Аналогично, в двоичной системе разряды имеют степени, соответствующие степеням двойки.
Количество цифр в разряде и их значения влияют на значение числа. Значение каждой цифры зависит от ее положения в разряде. Например, в десятичной системе цифра 2 в разряде десятков имеет значение 2 * 10^1 = 20, а в разряде единиц имеет значение 2 * 10^0 = 2.
Эта система, в которой количественный эквивалент цифры зависит от ее положения в записи числа, называется разрядной системой.
В каждой числовой системе разряды имеют свое обозначение. Например, в десятичной системе разряды обозначены цифрами от 0 до 9, в двоичной — цифрами 0 и 1, восьмеричной — цифрами от 0 до 7, и так далее.
Разряды и разрядный эквивалент являются важной концепцией в числовых системах с позиционным представлением и позволяют эффективно представлять и манипулировать числами различных величин и точности.
Примеры количественного эквивалента цифр
- В десятичной системе счисления, цифра 5, находящаяся в разряде единиц, имеет количественный эквивалент 5.
- В двоичной системе счисления, цифра 1, находящаяся в разряде единиц, имеет количественный эквивалент 1.
- В восьмеричной системе счисления, цифра 7, находящаяся в разряде единиц, имеет количественный эквивалент 7.
- В шестнадцатеричной системе счисления, цифра F, находящаяся в разряде единиц, имеет количественный эквивалент 15.
Когда цифры находятся в более высоких разрядах, их количественный эквивалент увеличивается в зависимости от их положения. Например, в десятичной системе, цифра 5, находящаяся в разряде десятков, имеет количественный эквивалент 50.
Таким образом, в различных системах счисления количественный эквивалент цифр зависит от их положения в записи числа и может иметь различные значения.
Важность понимания эквивалента цифр в записи числа
Понимание этой особенности является важным элементом при работе с числами. Оно помогает человеку правильно интерпретировать числовую информацию и выполнять математические операции.
Рассмотрим пример. В десятичной системе счисления число 253 состоит из трех цифр: 2, 5 и 3. При записи числа 253, цифра 3 находится в единичном разряде, цифра 5 — в десятичном разряде, и цифра 2 — в сотни. Таким образом, количественный эквивалент каждой цифры зависит от ее положения в записи числа. В данном случае, число 253 равно 200 + 50 + 3.
Понимание эквивалента цифр в записи числа играет ключевую роль не только в математике, но и в других областях, таких как программирование, физика, экономика и многое другое. К примеру, в программировании необходимо правильно использовать разряды числа при выполнении операций или преобразованиях.
Таким образом, понимание эквивалента цифр в записи числа является неотъемлемой частью математического образования и является фундаментальным навыком для эффективной работы с числовыми данными.
| Пример | 2 | 5 | 3 |
| Разряд | Сотни | Десятки | Единицы |
| Эквивалент | 200 | 50 | 3 |
Вопрос-ответ:
Что такое система, в которой количественный эквивалент цифры зависит от ее положения в записи числа?
Эта система называется позиционная система счисления.
Какая система счисления использует позиционную систему?
В основном, позиционная система используется в десятичной, двоичной, восьмеричной и шестнадцатеричной системах счисления.
Как работает позиционная система счисления?
В позиционной системе счисления значение цифры определяется не самой цифрой, а ее положением в числе. Каждая цифра в числе имеет свое место, и с помощью этого положения определяется ее количественное значение.
Какие преимущества имеет позиционная система счисления?
Позиционная система счисления позволяет представлять большие числовые значения с помощью ограниченного набора символов. Она также облегчает выполнение арифметических операций, так как основывается на принципе суммирования и умножения столбиком.