Правильным треугольником называют такой треугольник, у которого все три стороны равны и все три угла равны 60 градусов. Такой треугольник является одной из основных фигур в геометрии и обладает рядом интересных свойств.
Правильный треугольник является симметричной фигурой, у которой все три биссектрисы и медианы совпадают с медианами и биссектрисами. Это позволяет использовать правильные треугольники в решении геометрических задач и построения сложных фигур.
Кроме того, правильные треугольники обладают особым соотношением между длиной сторон и углом. Так, например, в правильном треугольнике со стороной длиной 1 единица, радиус описанной окружности будет равен 1, а площадь треугольника будет равна (корень из 3) делить на 4.
Геометрическую фигуру
Различные типы геометрических фигур включают в себя линии, точки, окружности, треугольники, квадраты, прямоугольники, параллелограммы, трапеции, ромбы, шестиугольники и многоугольники.
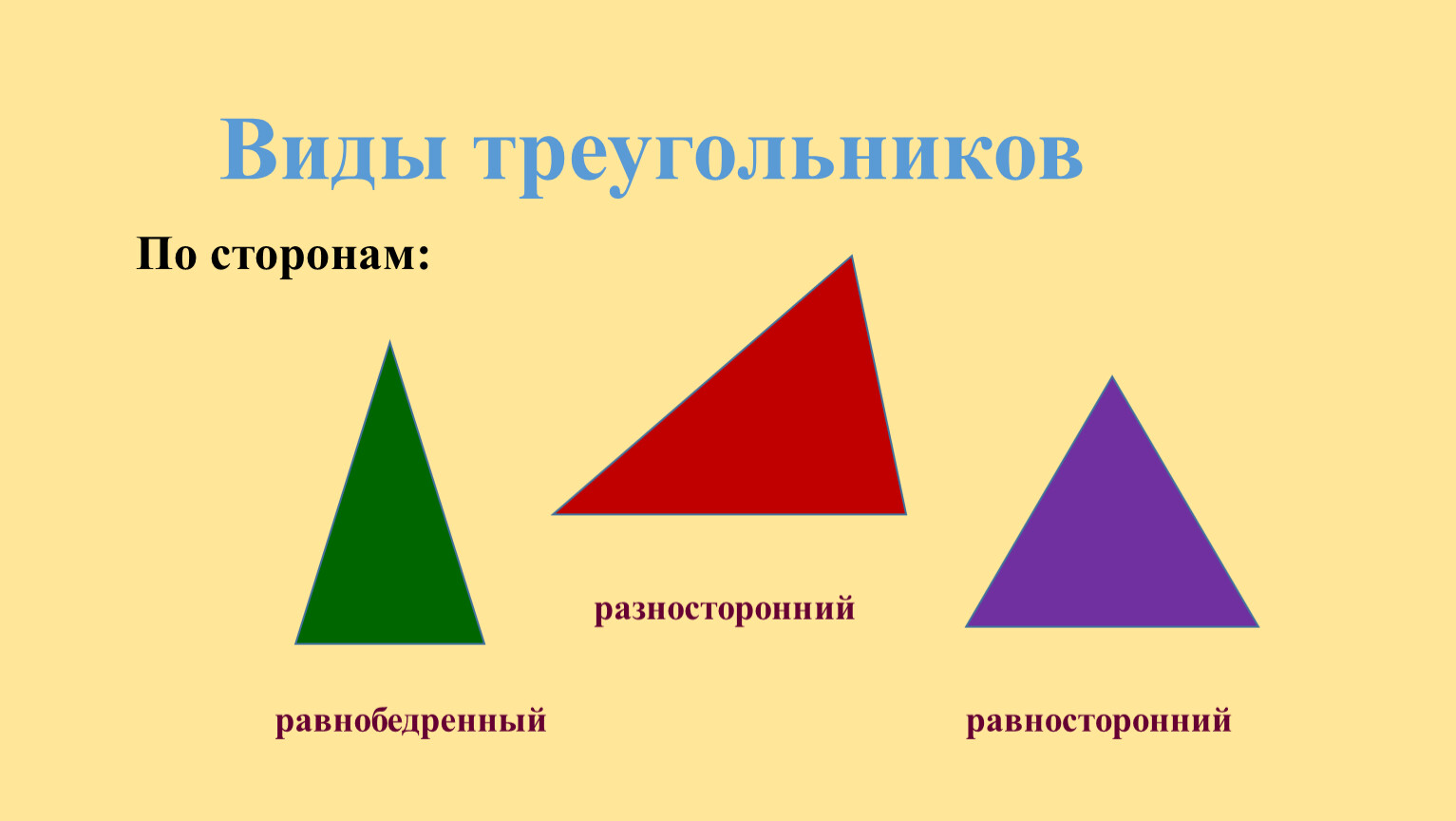
Каждая геометрическая фигура имеет свои характеристики и свойства. Например, треугольник — это геометрическая фигура с тремя сторонами и тремя углами. Существуют различные типы треугольников, такие как равносторонний треугольник, равнобедренный треугольник и разносторонний треугольник.
Геометрические фигуры часто используются в математике, физике, инженерии, архитектуре и других науках. Они помогают нам понять и описать мир вокруг нас, а также решать различные задачи и проблемы.
Треугольник, у которого
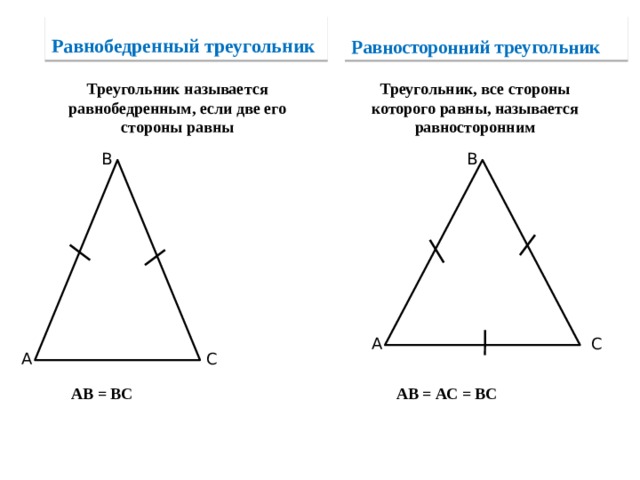
Кроме того, существуют треугольники, у которых две стороны равны между собой. Эти треугольники называются равнобедренными. В равнобедренном треугольнике углы, противолежащие равным сторонам, равны между собой.
А еще есть треугольник, у которого все три угла равны между собой и составляют по 60 градусов. Такой треугольник называется равноугольным. В равноугольном треугольнике все стороны также равны между собой.
Наконец, существует треугольник, у которого все три стороны имеют разные длины и все три угла разные. Этот треугольник называется разносторонним.
Зная эти основные виды треугольников, можно легко определить, к какому типу он относится по данным его сторонам и углам.
Все стороны равны
Если все стороны треугольника равны друг другу, то такой треугольник называется равносторонним.
Равносторонний треугольник имеет следующие свойства:
- Все его стороны имеют одинаковую длину.
- Все его углы равны между собой и равны 60 градусам.
- Проведенная из одной из вершин треугольника высота является медианой и биссектрисой.
Равносторонний треугольник обладает особыми свойствами и часто используется в геометрии и строительстве.
Углы внутри треугольника
Внутри правильного треугольника сумма всех его углов равна 180 градусам.
Так как в правильном треугольнике все стороны равны, то все его углы также равны между собой. Каждый угол составляет по 60 градусов.
Однако, в общем случае, углы внутри треугольника могут иметь любое значение и зависят от длин его сторон и их взаимного положения.
В треугольнике сумма всех его углов всегда равна 180 градусам. Существуют различные виды треугольников в зависимости от значений их углов:
- Остроугольный треугольник – все углы менее 90 градусов
- Тупоугольный треугольник – один из углов больше 90 градусов
- Прямоугольный треугольник – один из углов равен 90 градусов
Углы внутри треугольника играют важную роль при решении различных геометрических задач. Знание свойств углов позволяет определить тип треугольника, построить треугольник по заданным углам и сторонам, а также решать задачи на нахождение неизвестных значений углов и сторон треугольника.
Равны 60 градусам
Правильным треугольником называется треугольник, у которого все три угла равны 60 градусам. Такой треугольник также имеет все стороны равными между собой.
Если в треугольнике все углы равны 60 градусам, значит каждый угол равен одному третьему от 180 градусов – суммы всех углов равностороннего треугольника.
Такие треугольники играют важную роль в геометрии и имеют множество интересных свойств. Одно из этих свойств заключается в том, что в правильном треугольнике высота, проведенная из вершины, делит его на два равных прямоугольных треугольника.
Также в правильном треугольнике радиус вписанной окружности равен половине стороны треугольника, а радиус описанной окружности равен длине стороны треугольника, умноженной на √3.
Правильные треугольники являются основой для строительства различных геометрических конструкций и применяются в различных научных и технических областях, таких как архитектура, физика и программирование.
Свойства правильного треугольника
Правильным треугольником называется треугольник, у которого все стороны и углы равны. Такой треугольник имеет ряд интересных свойств, которые отличают его от обычных треугольников.
Свойство 1: Равные стороны
У правильного треугольника все стороны равны между собой. То есть, если обозначить длины сторон треугольника как a, b и c, то будет выполняться равенство a = b = c. Это делает его особенным и симметричным.
Свойство 2: Равные углы
Углы в правильном треугольнике также равны между собой. Каждый угол составляет 60 градусов. Таким образом, сумма всех углов в правильном треугольнике составляет 180 градусов.
Такие особенности правильного треугольника делают его удобным объектом для изучения геометрии и выполнения различных вычислений. Кроме того, он является базовой формой для построения других правильных многогранников, таких как правильные четырехугольники, пятиугольники и так далее.
Периметр и площадь
Периметр правильного треугольника
Периметр правильного треугольника можно вычислить, зная длину одной его стороны. Для этого нужно умножить длину стороны на 3, так как у правильного треугольника все стороны равны. Таким образом, формула для вычисления периметра равна:
Периметр = длина стороны × 3
Площадь правильного треугольника
Площадь правильного треугольника можно вычислить, зная длину его стороны. Для этого нужно воспользоваться следующей формулой:
Площадь = (длина стороны × длина стороны × √3) / 4
Где √3 — это квадратный корень из числа 3.
Зная длину стороны, можно легко вычислить периметр и площадь правильного треугольника.
Примеры и применение
Правильные треугольники имеют множество применений в различных областях. Вот несколько примеров:
1. Геометрия
В геометрии правильные треугольники служат основой для изучения свойств треугольников в целом. Они являются основным типом треугольников, имеющих равные стороны и углы. Изучение их свойств помогает понять основные концепции геометрии, такие как равенство углов, теорема Пифагора и законы синусов и косинусов.
2. Архитектура
Правильные треугольники широко используются в архитектуре. Они могут быть в основе архитектурных элементов, таких как углы зданий или оконные рамы. Использование правильных треугольников в архитектуре позволяет создать устойчивую и симметричную структуру.
Также, правильные треугольники могут быть использованы в расчетах и проектировании с учетом пропорций и углов зданий и сооружений.
3. Инженерия
В инженерии правильные треугольники часто используются для решения различных задач, связанных с измерениями и расчетами. Например, они могут быть использованы для определения расстояний и высоты объектов, расчета углов наклона скатов и рельсов, а также для создания устойчивых и прочных конструкций.
Также, правильные треугольники могут быть полезны для решения производственных задач, таких как расположение оборудования и компонентов внутри производственных помещений.
4. Информатика и графика
В информатике и графике правильные треугольники используются для создания и отображения геометрических фигур. Они могут быть использованы для создания трехмерных моделей и анимации, а также для создания текстур и паттернов на графических объектах.
Также, правильные треугольники широко применяются в алгоритмах компьютерного зрения, обработке изображений и машинном обучении для распознавания и классификации объектов на основе их формы и углов.
В таблице ниже приведены примеры некоторых использований правильных треугольников в различных областях:
| Область | Примеры применения |
|---|---|
| Геометрия | Изучение свойств треугольников, расчеты углов и сторон |
| Архитектура | Определение углов зданий, создание пропорций и симметрии |
| Инженерия | Расчеты высоты и расстояний, проектирование устойчивых конструкций |
| Информатика и графика | Создание трехмерных моделей, распознавание и классификация объектов |
Вопрос-ответ:
Что такое правильный треугольник?
Правильным треугольником называют треугольник, у которого все три стороны и все три угла равны друг другу. В нем все углы равны 60 градусов.
Какое свойство имеют стороны правильного треугольника?
Все стороны правильного треугольника равны между собой.
Как определить, что треугольник является правильным?
Для того чтобы треугольник был правильным, необходимо, чтобы все его стороны были равны между собой и все его углы были равны 60 градусов.
Какие примеры правильных треугольников вы знаете?
Примерами правильных треугольников являются треугольники со сторонами длиной 1, 2, 3 единицы или со сторонами длиной 10, 10, 10 единиц.
Какое значение имеют углы правильного треугольника?
Все углы правильного треугольника равны между собой и составляют 60 градусов.
Что такое правильный треугольник?
Правильным треугольником называется треугольник, у которого все стороны и все углы равны между собой.