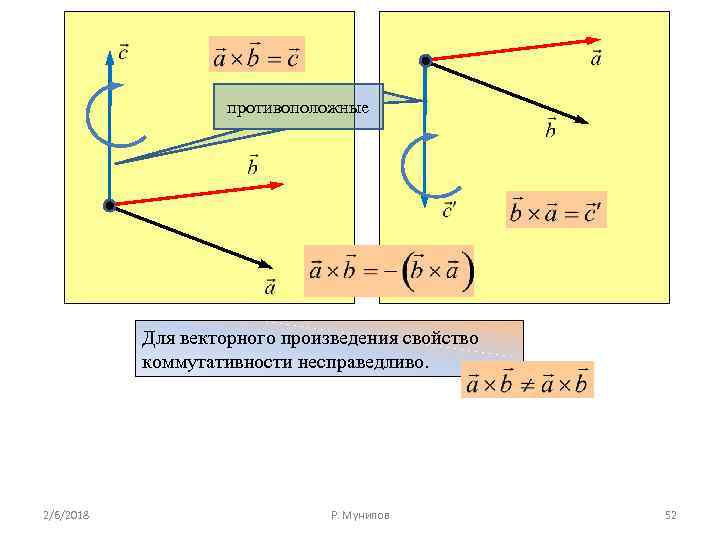
Векторы являются важной частью математики и физики, их понимание позволяет лучше разбираться во многих явлениях и законах природы. Одним из важных понятий векторного анализа является противоположность векторов.
Вектор называется противоположным другому вектору, если они имеют одинаковую длину, но направлены в противоположные стороны. Другими словами, если один вектор направлен вправо, то противоположный ему вектор будет направлен влево.
Противоположные векторы имеют несколько свойств. Во-первых, их сумма равна нулевому вектору. Второе свойство заключается в том, что угол между противоположными векторами составляет 180 градусов, что является максимально возможным значением угла между векторами.
Когда векторы называются противоположными?
Векторы называются противоположными, когда они имеют одинаковую длину, направлены в противоположные стороны и лежат на одной прямой.
Противоположные векторы характеризуются тем, что их сумма равна нулевому вектору. Если вектору A соответствует противоположный ему вектор -A, то их сумма A + (-A) будет равна нулевому вектору O.
Сумма двух противоположных векторов образует вектор, который равен нулю как по величине, так и по направлению. Нулевой вектор O является уникальным и не имеет определенного направления, поэтому векторы A и -A считаются противоположными.
Кроме того, противоположные векторы могут быть отмечены с помощью знака минус перед их названием. Например, вектор А и его противоположный вектор можно записать как A и -A соответственно.
Пример:
Допустим, имеется вектор А, направленный вправо и имеющий длину 5 единиц. Его противоположный вектор -А будет направлен влево и также иметь длину 5 единиц. Оба вектора будут лежать на одной прямой, при этом сумма векторов A + (-A) будет равна нулевому вектору O.
Таким образом, когда векторы имеют одинаковую длину, противоположное направление и лежат на одной прямой, они называются противоположными.
Определение противоположности векторов
Противоположными называются векторы, которые имеют равную длину, но противоположные направления. Если задан вектор A и его противоположный вектор обозначается как -A, то получим вектор, который имеет все те же характеристики, но противоположные значения.
Векторы могут быть представлены в виде графических объектов или математических сущностей, но их основные свойства все равно остаются неизменными. При суммировании векторов, противоположные векторы «сокращаются» и в результате получается вектор нулевой длины.
Например, если у нас есть вектор A = (1, 2) и его противоположный вектор -A = (-1, -2), их сумма будет равна (0, 0). Это объясняет, почему противоположные векторы сокращаются при сложении.
Использование противоположных векторов может быть полезно в различных областях науки и техники. Например, при расчете силы тяжести, противоположный вектор используется для вычисления силы противодействия. В физике противоположные векторы также используются для определения наличия баланса сил в системе.
Поэтому понимание противоположности векторов является важным аспектом в изучении физики, математики и других научных дисциплин, где векторы широко используются.
Общие характеристики противоположных векторов
Основные характеристики противоположных векторов:
- Одинаковая длина: Противоположные векторы имеют абсолютно одинаковую длину, но направление одного из них отличается от направления другого.
- Противоположные направления: Противоположные векторы всегда указывают в разные стороны. Когда один вектор направлен вверх, другой будет направлен вниз, и наоборот.
- Общая точка начала: У противоположных векторов оба конца совпадают, они имеют одну и ту же точку начала.
Противоположные векторы можно представить с помощью математических выражений, в которых один вектор равен другому, умноженному на -1.
Противоположные векторы играют важную роль в физике, математике и других областях науки. Они используются для описания движения, силы и других физических явлений. Также они помогают в определении расстояний, направлений и взаимного отношения векторов друг к другу.
Свойства противоположных векторов
Определение
Векторы называются противоположными, если они имеют одинаковую длину, но противоположные направления. Другими словами, если вектор A имеет направление, противоположное направлению вектора B, и их длины равны, то они считаются противоположными векторами.
Свойства
Противоположные векторы имеют следующие свойства:
- Сумма противоположных векторов равна нулевому вектору: A + (-A) = 0, где A — произвольный вектор.
- Противоположный вектор обладает той же длиной, но противоположным направлением.
- Скалярное произведение противоположных векторов равно произведению их длин на -1: A · (-A) = -|A| · |A| = -|A|^2, где A — произвольный вектор.
Использование свойств противоположных векторов позволяет упростить решение многих задач в физике, математике и других дисциплинах, где используются векторы.
Физический пример противоположных векторов
Противоположные векторы в физике часто используются для описания движения и сил. Например, представьте себе два вектора, которые описывают движение тела в противоположных направлениях. Если один вектор описывает движение вперед, то противоположным ему будет вектор, описывающий движение назад.
Другой пример — силы, действующие на тело. Если на тело действуют две силы, но они направлены в противоположные стороны, то суммарная сила будет равна нулю. Это означает, что эти две силы являются противоположными векторами.
Противоположные векторы имеют равные по модулю значения, но противоположные направления. Они отображаются в виде векторов с равными длинами, но противоположными стрелками.
Физический пример противоположных векторов помогает лучше понять понятие противоположности векторов и их важность в физических расчетах и моделировании.
Алгебраическое определение противоположности векторов
Противоположными называются векторы, которые имеют одинаковую длину, но направлены в противоположные стороны. Математически это выражается следующим образом:
Пусть даны два вектора а и б. Если сумма векторов равна нулевому вектору, то векторы называются противоположными. Формально это можно записать так:
| Определение | Противоположные векторы |
|---|---|
| Вектор | а и б |
| Сумма векторов | а + б = 0 |
Таким образом, если векторы имеют равную по модулю, но противоположную по направлению величину и при сложении дают нулевой вектор, они считаются противоположными.
Пример:
Пусть даны два вектора: а = (3, -2) и б = (-3, 2). Оба вектора имеют длину √(3^2 + (-2)^2) = √(13), но направлены в противоположные стороны. При сложении векторов получаем (3 + (-3), -2 + 2) = (0, 0), что является нулевым вектором. Значит, векторы а и б являются противоположными.
Алгебраическое определение противоположности векторов позволяет устанавливать связь между величинами и направлениями векторов и использовать ее при решении задач в различных областях науки и техники.
Геометрическое представление противоположных векторов
Геометрически противоположные векторы отображаются на координатной плоскости следующим образом:
- Выбирается начало координат, обозначается точкой O.
- Противоположные векторы имеют одинаковую длину, поэтому нарисуем два равных по длине отрезка, например, от точки O до точки A и от точки O до точки B.
- Отрезок OA будет положительным вектором, а отрезок OB – противоположным вектором.
- Противоположные векторы имеют противоположные направления, поэтому отрезок OB будет направлен в противоположную сторону от отрезка OA.
Таким образом, геометрически противоположные векторы отображаются на координатной плоскости как два равных по длине, но направленных в противоположные стороны отрезка, начинающегося в начале координат.
Применение противоположных векторов в разных областях
Применение противоположных векторов широко распространено в различных областях, включая физику, математику, компьютерную графику и другие. Ниже приведены примеры использования противоположных векторов в этих областях:
-
Физика: В физике противоположные векторы используются для обозначения движения и силы. Например, вектор силы, действующей на тело, и вектор противоположной силы, которая действует в противоположном направлении. Это позволяет определить равновесие и несбалансированное движение тела.
-
Математика: В математике противоположные векторы используются для выполнения операций сложения и вычитания векторов. Если векторы имеют одинаковые направления, но противоположные по модулю, то их сумма будет равна нулевому вектору. Это позволяет решать задачи на определение направления и величины вектора при выполнении операций.
-
Компьютерная графика: В компьютерной графике противоположные векторы используются для вычисления освещения и теней. Например, для создания реалистичного освещения объекта, используются векторы нормалей, которые указывают на направление света. Противоположные нормали используются для создания теней и отражений.
Применение противоположных векторов позволяет точнее моделировать реальные явления и решать сложные задачи в разных областях. Их использование имеет фундаментальное значение для развития науки и технологии.
Примеры использования противоположных векторов
1. Математика
В математике противоположные векторы используются для определения отрицания или противоположного значения. Например, если вектор имеет координаты (3, 4), то его противоположным вектором будет вектор с координатами (-3, -4).
2. Физика
В физике противоположные векторы могут использоваться для представления противоположных сил или движений. Например, если сила, действующая на тело, равна 10 Н, то противоположной ей будет сила равная -10 Н, направленная в противоположную сторону.
Это примеры использования противоположных векторов в разных областях. Знание и понимание этих понятий позволяет более точно и полно описывать и анализировать различные явления и процессы.
Вопрос-ответ:
Какие векторы можно назвать противоположными?
Противоположными называются векторы, которые имеют одинаковую длину, но направлены в разные стороны. Если векторы A и B противоположны, то A = -B и B = -A.
Какое свойство у противоположных векторов?
Основное свойство противоположных векторов — их сумма равна нулевому вектору. Если A и B — противоположные векторы, то A + B = 0.
Можно ли назвать векторы противоположными, если их длины отличаются?
Для того чтобы векторы считались противоположными, должно выполняться условие, что они имеют равные длины, но противоположные направления. Поэтому векторы с разными длинами не являются противоположными.
Как узнать, что два вектора являются противоположными?
Чтобы узнать, что два вектора являются противоположными, нужно проверить условие: они должны иметь одинаковую длину и противоположные направления. Если это условие выполняется, то векторы являются противоположными.
Каким образом можно представить противоположный вектор к данному?
Чтобы найти противоположный вектор к данному, необходимо изменить его направление на обратное, а длину оставить неизменной. Для этого можно умножить координаты вектора на -1.
Что такое противоположные векторы?
Противоположные векторы — это два вектора, которые имеют одинаковую длину и направление, но противоположные по своей сущности. Иными словами, если вектор A указывает в одном направлении, то противоположный ему вектор -A будет указывать в противоположном направлении.
Как определить, что векторы являются противоположными друг другу?
Два вектора считаются противоположными друг другу, если они имеют одинаковую длину и направление, но противоположные знаки координат или противоположные знаки их компонентов. Например, если первый вектор имеет координаты (2, -3, 5), то второй вектор будет противоположным ему, если его координаты будут (-2, 3, -5).