
Одно из основных понятий геометрии — расстояние между скрещивающимися прямыми. Оно является важным инструментом для измерения расстояния между двумя параллельными прямыми и определения их взаимного положения.
Расстояние между скрещивающимися прямыми можно определить с использованием нескольких методов, включая использование формулы расстояния между точкой и прямой, используя формулу для нахождения расстояния между двумя параллельными прямыми или с помощью использования теоремы Пифагора.
Особое внимание следует уделить вычислению расстояния между двумя параллельными прямыми. Для этого можно использовать формулу, обеспечивающую точное измерение данного расстояния. При этом, необходимо знать коэффициент наклона каждой из прямых и расстояние между ними по вертикали или горизонтали.
Знание и умение определять расстояние между скрещивающимися прямыми играет важную роль в различных областях, таких как инженерия, архитектура, строительство, компьютерная графика и многое другое. Поэтому, понимание и применение этого понятия является неотъемлемой частью геометрии и обеспечивает точные и надежные результаты в вычислениях и проектировании.
Определение расстояния между скрещивающимися прямыми
Для определения расстояния между скрещивающимися прямыми необходимо знать уравнения данных прямых. После определения точки скрещивания, можно провести отрезок между этой точкой и любой другой точкой на одной из прямых. Длина этого отрезка будет являться расстоянием между прямыми и может быть выражена числовым значением.
Определение расстояния между скрещивающимися прямыми может быть полезно в различных областях, таких как геометрия, астрономия, а также в инженерии и строительстве. Например, в строительстве расстояние между скрещивающимися прямыми может означать ширину дороги или расстояние между зданиями.
Что такое расстояние между скрещивающимися прямыми
Расстояние между скрещивающимися прямыми может быть положительным или отрицательным, в зависимости от направления перпендикуляра. Если перпендикуляр направлен в одну сторону от пересечения прямых, то расстояние считается положительным. Если перпендикуляр направлен в другую сторону — расстояние считается отрицательным.
Расстояние между скрещивающимися прямыми играет важную роль в различных областях, таких как геометрия, физика, инженерия и дизайн. Оно позволяет определить геометрические свойства прямых (например, их относительное положение и углы между ними) и применять эти знания в решении различных задач и задачей нахождения расстояния до объекта.
Формула для вычисления расстояния между скрещивающимися прямыми
Шаг 1: Изучение прямых
Перед тем, как начать вычислять расстояние между скрещивающимися прямыми, необходимо изучить характеристики самих прямых. Для каждой прямой необходимо знать её угловой коэффициент, который обозначается как k. Также необходимо знать точку пересечения прямых, которая обозначается как (a, b).
Шаг 2: Применение формулы
После определения характеристик прямых можно приступить к вычислению расстояния между ними. Для этого используется следующая формула:
d = |b — a / √(k2 + 1)|
где d — искомое расстояние, a и b — координаты точки пересечения прямых, k — угловой коэффициент одной из прямых.
Результат вычислений будет являться неотрицательным числом, так как используется модуль в формуле.
Пример расчета расстояния между скрещивающимися прямыми
Допустим, у нас есть две скрещивающиеся прямые, заданные уравнениями:
Прямая 1: y = ax + b1
Прямая 2: y = cx + b2
Чтобы найти расстояние между этими прямыми, мы будем использовать формулу:
d = |b2 — b1| / √(a^2 + c^2)
Где:
- d — расстояние между прямыми
- |b2 — b1| — модуль разности свободных коэффициентов b2 и b1
- √(a^2 + c^2) — квадратный корень из суммы квадратов коэффициентов a и c
Приведем пример:
Пусть прямая 1 задана уравнением y = 2x + 3, а прямая 2 — уравнением y = -3x + 6.
Тогда:
a = 2
b1 = 3
c = -3
b2 = 6
Подставим эти значения в формулу:
d = |6 — 3| / √((2)^2 + (-3)^2) = 3 / √(4 + 9) = 3 / √13 ≈ 0.83
Таким образом, расстояние между прямыми y = 2x + 3 и y = -3x + 6 составляет примерно 0.83 единицы.
Значение расстояния между скрещивающимися прямыми в геометрии
В геометрии расстояние между скрещивающимися прямыми играет важную роль при решении различных задач и конструкций. Расстояние между двумя скрещивающимися прямыми определяется как длина перпендикулярного отрезка, проведенного между ними.
Для определения расстояния между скрещивающимися прямыми можно использовать различные методы. Один из них — использование уравнения прямой и формулы расстояния между двумя точками. Если уравнения прямых даны в виде y = k1x + b1 и y = k2x + b2, то расстояние между ними можно найти по формуле:
d = |b2 — b1| / sqrt(k1^2 + k2^2)
Если уравнения прямых даны в параметрическом виде, то расстояние между ними можно определить, найдя точку пересечения прямых и вычислив расстояние от этой точки до каждой из прямых.
Значение расстояния между скрещивающимися прямыми может быть положительным или отрицательным, в зависимости от свойств прямых и их взаимного расположения. В случае, если прямые параллельны, расстояние между ними принимает бесконечное значение.
Свойства расстояния между скрещивающимися прямыми
Важно отметить следующие свойства расстояния между скрещивающимися прямыми:
| 1. | Расстояние между скрещивающимися прямыми всегда положительно и не может быть отрицательным. Это связано с определением расстояния как положительного числа, которое показывает длину отрезка между двумя точками. |
| 2. | Если скрещивающиеся прямые параллельны, то их расстояние равно бесконечности. Это свойство следует из определения параллельных прямых, которые никогда не пересекаются и, следовательно, расстояние от одной до другой будет бесконечным. |
| 3. | Расстояние между скрещивающимися прямыми можно выразить в виде модуля уравнения прямой. Модуль отрицательного числа равен его абсолютной величине, поэтому это свойство позволяет нам рассчитать расстояние независимо от знака. |
| 4. | Если расстояние между скрещивающимися прямыми равно нулю, то это означает, что прямые совпадают. Это возможно только в случае одинаковых прямых, когда они идентичны и не пересекаются в точке. |
| 5. | Расстояние между скрещивающимися прямыми может быть найдено с использованием различных методов, включая геометрические построения, формулы или аналитическую геометрию. Подходящий метод выбирается в зависимости от доступной информации и требуемой точности результата. |
Изучение и понимание свойств расстояния между скрещивающимися прямыми позволяет анализировать геометрические конструкции и решать разнообразные задачи, связанные с прямыми и плоскостью.
Приложения расстояния между скрещивающимися прямыми в реальной жизни
Дорожное строительство
При планировании и строительстве дорог, знание расстояния между скрещивающимися прямыми помогает инженерам оптимизировать геометрию перекрестков и оценить необходимое пространство для поворотов и размещения сигнальных установок. Это позволяет увеличить безопасность и эффективность движения транспорта.
Конструкционное проектирование
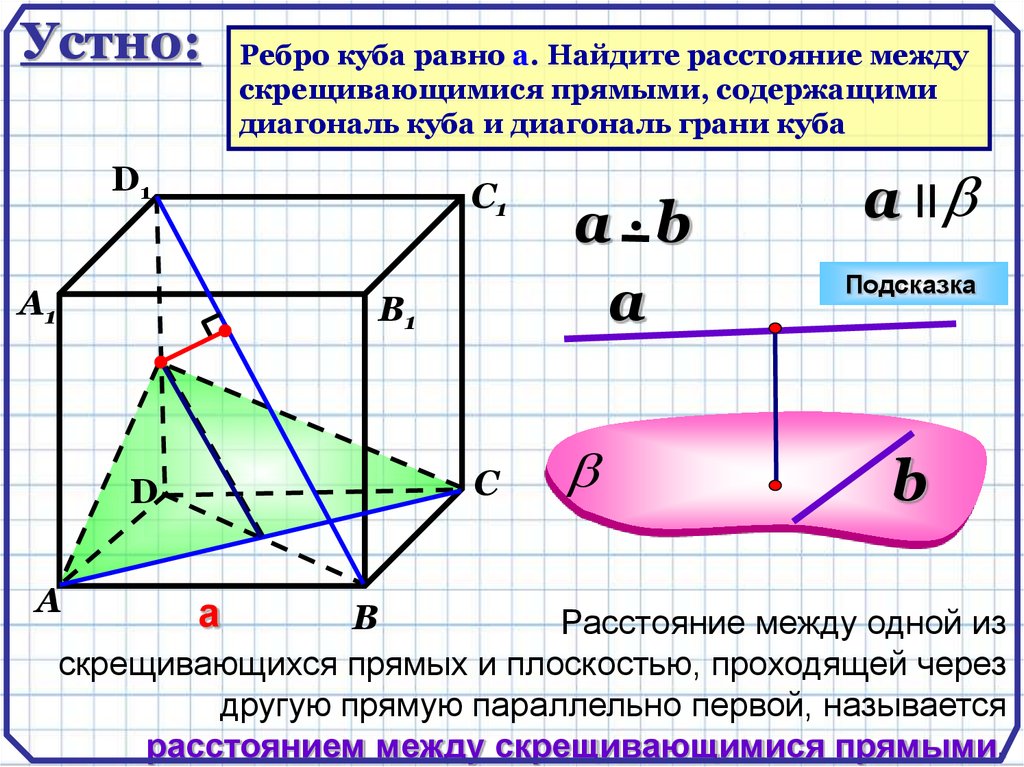
В процессе создания различных конструкций, расстояние между скрещивающимися прямыми используется для определения размеров и формы элементов. Например, при проектировании зданий и мостов, знание этого расстояния позволяет учесть необходимую прочность и стабильность конструкции.
Кроме того, расстояние между скрещивающимися прямыми находит применение в топографии, космических исследованиях, построении графиков и многих других областях, где важна точная геометрическая информация.
Как использовать расстояние между скрещивающимися прямыми для решения задач
Расстояние между скрещивающимися прямыми может быть полезно для определения положения точек, лежащих на прямых, а также для построения треугольников, параллелограммов и других фигур в пространстве.
Для использования этого расстояния в решении задач, вам необходимо знать уравнения скрещивающихся прямых и точку, в которой они пересекаются. Сначала определите точку пересечения прямых, затем вычислите расстояние между этой точкой и любой другой точкой, лежащей на одной из прямых.
Для вычисления расстояния между точками на прямой вы можете использовать формулу расстояния между двумя точками:
- Определите координаты двух точек на одной из прямых.
- Используя формулу расстояния между двумя точками, вычислите расстояние между этими точками.
- Повторите шаги 1-2 для другой точки на прямой.
- Получите два значения расстояния между точками на одной прямой.
- Найдите минимальное значение из двух расстояний — это будет расстояние между скрещивающимися прямыми.
Таким образом, использование расстояния между скрещивающимися прямыми позволяет решать различные задачи, связанные с прямыми и их пересечением. Оно может быть полезно для определения положения точек, построения геометрических фигур и решения задач аналитической геометрии и статики.
Вопрос-ответ:
Какое определение имеет расстояние между скрещивающимися прямыми?
Расстояние между скрещивающимися прямыми — это расстояние между точкой пересечения двух прямых и какой-либо точкой, лежащей на одной из прямых.
Можно ли вычислить расстояние между скрещивающимися прямыми, зная их уравнения?
Да, для вычисления расстояния между скрещивающимися прямыми можно использовать их уравнения. Для этого необходимо найти точку пересечения прямых и затем найти расстояние от этой точки до любой другой точки на одной из прямых.
Какое значение имеет расстояние между скрещивающимися прямыми?
Расстояние между скрещивающимися прямыми используется для измерения физических, геометрических или абстрактных величин. Оно может описывать расстояние между объектами на плоскости или в пространстве, а также использоваться в различных математических и физических моделях.
Как можно определить, скрещиваются ли две прямые?
Для определения того, скрещиваются ли две прямые, необходимо решить систему уравнений, составленную из уравнений данных прямых. Если система имеет решение, то прямые скрещиваются, если система не имеет решения, то прямые параллельны, и если система имеет бесконечно много решений, то прямые совпадают.