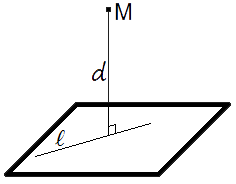
Расстояние от точки до плоскости – величина, которая определяет минимальное расстояние между точкой и плоскостью. Эта важная концепция применяется в различных областях знаний, включая геометрию, физику и робототехнику. Знание формулы для вычисления расстояния от точки до плоскости позволяет определить, как близко находится точка к плоскости и решить множество задач, связанных с этими объектами.
Для вычисления расстояния от точки до плоскости можно использовать известную формулу, основанную на применении векторов и нормали плоскости. Вектор нормали к плоскости перпендикулярен к плоскости и указывает направление наибольшего увеличения расстояния от плоскости. Проекция вектора, соединяющего точку с плоскостью, на вектор нормали дает расстояние от точки до плоскости. Это позволяет учесть и направление расстояния – точка может находиться как «внутри» плоскости, так и «снаружи».
Пример вычисления расстояния от точки до плоскости:
Пусть дана точка A(2, 5, -1) и плоскость, заданная нормалью n(1, 1, 1) и точкой на плоскости B(0, 0, 0). Необходимо найти расстояние от точки А до плоскости. Для решения этой задачи мы используем формулу расстояния от точки до плоскости:
d = |(AX * n)| / |n|,
где d — расстояние, AX — вектор, соединяющий точку А и точку на плоскости B, n — вектор нормали к плоскости. Применяя данную формулу, мы получим:
d = |(AX * n)| / |n| = |((2, 5, -1) — (0, 0, 0)) * (1, 1, 1)| / |(1, 1, 1)| = |(2, 5, -1) * (1, 1, 1)| / |(1, 1, 1)| = |(2 + 5 — 1)| / √(1^2 + 1^2 + 1^2) = 6 / √3 ≈ 3.46.
Таким образом, расстояние от точки A до плоскости составляет приблизительно 3.46 единицы длины.
Определение расстояния от точки до плоскости
Для вычисления расстояния от точки до плоскости используются математические формулы и координаты точки в пространстве. Одна из наиболее распространенных формул для рассчета расстояния от точки до плоскости основана на использовании уравнения плоскости и координат точки:
d = |Ax + By + Cz + D| / sqrt(A^2 + B^2 + C^2)
Здесь d обозначает расстояние от точки до плоскости, (x, y, z) – координаты точки, A, B, C и D – коэффициенты уравнения плоскости.
Пример вычисления расстояния от точки до плоскости может быть следующим. Рассмотрим плоскость с уравнением 2x + 3y + 4z — 12 = 0 и точку с координатами (1, 2, 3). Для вычисления расстояния, подставим значения в формулу:
d = |2*1 + 3*2 + 4*3 — 12| / sqrt(2^2 + 3^2 + 4^2) = 1 / sqrt(29)
Таким образом, расстояние от точки с координатами (1, 2, 3) до плоскости 2x + 3y + 4z — 12 = 0 равно 1 / sqrt(29).
Что такое расстояние от точки до плоскости?
Для вычисления расстояния от точки до плоскости используется формула, которая зависит от типа плоскости и её уравнения. Например, для плоскости с уравнением вида Ax + By + Cz + D = 0, где A, B, C и D — числа, расстояние до нее можно найти с помощью формулы:
d = |Ax + By + Cz + D| / √(A² + B² + C²)
где d — расстояние от точки до плоскости, x, y, z — координаты точки, A, B, C, D — числа из уравнения плоскости.
Найденное расстояние позволяет определить, находится ли точка на одной стороне плоскости или на другой. Если точка находится на этой плоскости, то расстояние равно нулю. Если точка находится на другой стороне плоскости, то расстояние положительное.
Примеры вычисления расстояния от точки до плоскости могут помочь лучше понять данное понятие.
Расстояние от точки до плоскости — это…
| Величина | Формула |
|---|---|
| Расстояние от точки до плоскости | d = |(AX + BY + CZ + D)| / sqrt(A^2 + B^2 + C^2) |
Где (X, Y, Z) — координаты заданной точки, A, B, C — коэффициенты уравнения плоскости, D — константа уравнения плоскости.
Для вычисления расстояния, необходимо знать координаты точки и уравнение плоскости, которой она принадлежит. Если точка находится над или под плоскостью, расстояние будет положительным. Если точка лежит в плоскости или находится на ней, расстояние будет равно нулю.
Примером вычисления расстояния от точки до плоскости может служить задача о нахождении расстояния от точки (2, 3, -1) до плоскости 2x + 3y — z = 5:
| Величина | Формула | Вычисление |
|---|---|---|
| Расстояние от точки до плоскости | d = |(2*2 + 3*3 + (-1)*(-1) — 5)| / sqrt(2^2 + 3^2 + (-1)^2) | d = |(4 + 9 + 1 — 5)| / sqrt(4 + 9 + 1) = |9| / sqrt(14) ≈ 9 / 3.74 ≈ 2.41 |
Таким образом, расстояние от точки (2, 3, -1) до плоскости 2x + 3y — z = 5 составляет примерно 2.41 единицы длины.
Как вычислить расстояние от точки до плоскости?
Для начала, найдем уравнение плоскости. Обычно плоскость задается уравнением вида Ax + By + Cz + D = 0, где A, B, C и D — это коэффициенты плоскости.
Затем, найдем расстояние от точки до плоскости с помощью формулы:
- Рассчитаем нормальный вектор плоскости, который равен [A, B, C].
- Найдем координаты проекции точки на плоскость с помощью следующей формулы:
X = x — (Ax + By + Cz + D) * A / (A^2 + B^2 + C^2)
Y = y — (Ax + By + Cz + D) * B / (A^2 + B^2 + C^2)
Z = z — (Ax + By + Cz + D) * C / (A^2 + B^2 + C^2)
- Рассчитаем расстояние между исходной точкой и проекцией на плоскость по формуле:
d = sqrt((x — X)^2 + (y — Y)^2 + (z — Z)^2)
Таким образом, используя данные формулы, можно достаточно точно вычислить расстояние от точки до плоскости. Этот подход широко применяется в различных областях, таких как физика, компьютерная графика и инженерия.
Формула для вычисления расстояния
Для определения расстояния от точки до плоскости существует специальная формула. Данная формула позволяет вычислить расстояние между заданной точкой и плоскостью, заданной уравнением.
Формула вычисления расстояния от точки P(x, y, z) до плоскости Ax + By + Cz + D = 0 имеет следующий вид:
d = |Ax + By + Cz + D| / sqrt(A^2 + B^2 + C^2)
Здесь d — искомое расстояние от точки до плоскости.
Данная формула основывается на понятии проекции точки на плоскость и евклидовой метрике. С помощью этой формулы можно точно определить расстояние между точкой и плоскостью в трехмерном пространстве.
Формула вычисления расстояния от точки до плоскости
Расстояние от точки до плоскости может быть определено с помощью специальной формулы. Для этого необходимо знать координаты точки и коэффициенты уравнения плоскости.
Предположим, что уравнение плоскости записано в виде Ax + By + Cz + D = 0, а координаты точки равны (x0, y0, z0). В таком случае, расстояние d от точки до плоскости может быть вычислено по следующей формуле:
| d = | |Ax0 + By0 + Cz0 + D| | / sqrt(A^2 + B^2 + C^2) |
Где:
- d — расстояние от точки до плоскости;
- A, B, C, D — коэффициенты уравнения плоскости;
- x0, y0, z0 — координаты точки.
Таким образом, зная координаты точки и коэффициенты уравнения плоскости, мы можем легко вычислить расстояние от данной точки до плоскости с помощью представленной формулы.
Пример вычисления расстояния от точки до плоскости
Допустим, у нас есть плоскость, заданная уравнением Ax + By + Cz + D = 0, где A, B и C — это коэффициенты плоскости, а x, y и z — координаты точки, от которой мы хотим найти расстояние.
Пусть дана точка P с координатами (x0, y0, z0), для которой мы хотим вычислить расстояние до плоскости. Тогда расстояние d можно вычислить по формуле:
d = |Ax0 + By0 + Cz0 + D| / √(A^2 + B^2 + C^2)
Найдем расстояние от точки P(2, 3, 4) до плоскости 2x + 3y — z — 6 = 0.
Подставим значения в формулу:
d = |2*2 + 3*3 — 4 — 6| / √(2^2 + 3^2 + (-1)^2)
d = |4 + 9 — 4 — 6| / √(4 + 9 + 1)
d = |3| / √(14)
Итак, расстояние от точки P(2, 3, 4) до плоскости 2x + 3y — z — 6 = 0 составляет 3 / √14 единиц.
Таким образом, мы вычислили расстояние от точки до плоскости с использованием формулы и привели пример расчета для конкретных значений.
Примеры вычисления расстояния от точки до плоскости
Для вычисления расстояния от точки до плоскости используется формула:
d = |ax + by + cz + d| / √(a^2 + b^2 + c^2),
где (x, y, z) — координаты точки, аx + by + cz + d = 0 — уравнение плоскости.
Пример 1:
Плоскость задана уравнением 2x + y — z + 3 = 0. Найти расстояние от точки P(1, -2, 4) до плоскости.
Подставляя значения координат точки и уравнения плоскости в формулу, получаем:
d = |2(1) + (-2)(-2) + (-4) + 3| / √(2^2 + 1^2 + (-1)^2) =
= |2 + 4 — 4 + 3| / √(4 + 1 + 1) = 5 / √6 ≈ 2.041
Расстояние от точки P до плоскости ≈ 2.041.
Пример 2:
Плоскость задана уравнением 3x — 3y + 2z — 6 = 0. Найти расстояние от точки Q(2, -1, 3) до плоскости.
Подставляя значения координат точки и уравнения плоскости в формулу, получаем:
d = |3(2) — 3(-1) + 2(3) — 6| / √(3^2 + (-3)^2 + 2^2) =
= |6 + 3 + 6 — 6| / √(9 + 9 + 4) = 9 / √22 ≈ 1.912
Расстояние от точки Q до плоскости ≈ 1.912.
Пример 3:
Плоскость задана уравнением x + 2y + 3z — 4 = 0. Найти расстояние от точки R(-3, 1, 2) до плоскости.
Подставляя значения координат точки и уравнения плоскости в формулу, получаем:
d = |(-3) + 2(1) + 3(2) — 4| / √(1^2 + 2^2 + 3^2) =
= |-3 + 2 + 6 — 4| / √(1 + 4 + 9) = 1 / √14 ≈ 0.267
Расстояние от точки R до плоскости ≈ 0.267.
Пример 1: Расстояние от точки до плоскости в трехмерном пространстве
Для вычисления расстояния от точки \(M\) до плоскости \(\pi\) воспользуемся формулой:
\[d = \frac{}{{\sqrt{a^2 + b^2 + c^2}}}\]
где \(d\) — искомое расстояние.
Рассмотрим пример. Пусть у нас есть плоскость \(\pi: 2x + 3y — z + 6 = 0\) и точка \(M(1, -2, 3)\). Найдем расстояние от точки \(M\) до плоскости \(\pi\).
Подставляя значения координат точки \(M\) и коэффициентов плоскости в формулу, получаем:
\[d = \frac}}{{\sqrt{14}}} = \frac{1}{{\sqrt{14}}}\]
Таким образом, расстояние от точки \(M(1, -2, 3)\) до плоскости \(\pi: 2x + 3y — z + 6 = 0\) равно \(\frac{1}{{\sqrt{14}}}\).
Вопрос-ответ:
Что такое расстояние от точки до плоскости?
Расстояние от точки до плоскости — это длина отрезка, соединяющего точку с ближайшей точкой плоскости. Это расстояние проецируется перпендикулярно на плоскость.
Как вычислить расстояние от точки до плоскости?
Для вычисления расстояния от точки до плоскости нужно найти проекцию этой точки на плоскость и измерить расстояние между этой проекцией и самой точкой. Можно использовать геометрические методы или формулу расстояния.
Как проверить правильность вычисления расстояния от точки до плоскости?
Если вы хотите проверить правильность вычисления расстояния от точки до плоскости, можно использовать геометрический подход. Постройте прямую линию между точкой и плоскостью, и убедитесь, что она перпендикулярна плоскости. Также можно сравнить результаты с другими вычислительными методами или использовать онлайн-калькуляторы для проверки.
Какие применения имеет расстояние от точки до плоскости?
Расстояние от точки до плоскости имеет множество применений в различных областях, включая геометрию, физику, компьютерную графику и инженерию. В геометрии оно помогает определить связь между точками и плоскостями. В физике оно используется для расчета расстояния от объекта до поверхности. В компьютерной графике оно применяется для создания трехмерных моделей и определения видимости объектов. В инженерии оно помогает в определении удаленности объекта от заданной плоскости.
Как определить расстояние от точки до плоскости?
Расстояние от точки до плоскости можно определить с помощью формулы, основанной на вычислении проекции вектора, соединяющего точку и плоскость, на нормальный вектор плоскости.