Треугольники — это геометрические фигуры, состоящие из трех сторон и трех углов. Они могут быть различных форм и размеров. Однако существуют треугольники, которые имеют сходственные черты. В геометрии такие треугольники называются сходственными.
Сходственные треугольники имеют равные соотношения между сторонами и углами. Они имеют одинаковую форму, но могут отличаться размером. Для того чтобы треугольники считались сходственными, необходимо, чтобы соотношения всех сторон и углов были равными.
Сходственные треугольники играют важную роль в геометрии, так как позволяют строить подобные фигуры и решать различные задачи. Они имеют множество свойств и правил, которые можно использовать в решении задач треугольников. Это помогает упростить анализ и вычисления, связанные с треугольниками.
Что такое сходственные треугольники?
Чтобы два треугольника были сходственными, необходимо, чтобы выполнялось одно из трех условий:
- Условие по сторонам: Если соответствующие стороны двух треугольников пропорциональны, то треугольники считаются сходственными. Например, если соотношение сторон треугольника А к соответствующим сторонам треугольника В равно соотношению сторон треугольника С к соответствующим сторонам треугольника В, то треугольники А и С сходственны.
- Условие по углам: Если соответствующие углы двух треугольников равны, то треугольники считаются сходственными. Например, если угол А треугольника А равен углу В треугольника В, а угол С треугольника А равен углу В треугольника В, то треугольники А и С сходственны.
- Условие по сторонам и углам: Если треугольники удовлетворяют обоим условиям по сторонам и углам, то они считаются сходственными. Например, если соотношение сторон треугольника А к соответствующим сторонам треугольника В равно соотношению сторон треугольника С к соответствующим сторонам треугольника В, и угол А треугольника А равен углу В треугольника В, а угол С треугольника А равен углу В треугольника В, то треугольники А и С сходственны.
Сходственные треугольники используются в геометрии для решения различных задач. Зная соотношения сторон и углов сходственных треугольников, можно находить неизвестные значения и определять свойства треугольников.
Определение сходственных треугольников
Сходственными треугольниками называются треугольники, у которых соответствующие углы равны, а соотношение длин сторон одинаково. Такие треугольники имеют одинаковую форму, но могут отличаться размерами.
Для определения сходственных треугольников можно использовать следующие признаки:
- Угловое сходство: если у треугольников все углы соответственно равны.
- Соотношение сторон: если отношение длин сторон одного треугольника к длинам соответствующих сторон другого треугольника одинаково.
Сходственные треугольники имеют много важных свойств и применяются в различных областях математики и геометрии. Например, эти треугольники позволяют строить сходственные фигуры, решать задачи на нахождение неизвестных сторон или углов, а также работать с пропорциями и подобиями.
Важно отличать сходственные треугольники от равных треугольников. Равные треугольники имеют абсолютно равные углы и стороны, в то время как сходственные треугольники имеют только соответствующие равные углы и одинаковое отношение длин сторон.
Как определить сходственные треугольники?

Сравнение сторон
Для сравнения сторон треугольников необходимо измерить их длины и сравнить их между собой. Если соответствующие стороны двух треугольников пропорциональны, то треугольники являются сходственными.
Сравнение углов
Для сравнения углов треугольников можно использовать геометрические инструменты, такие как угломер или транспортир. Измерив соответствующие углы треугольников, можно сравнить их между собой. Если соответствующие углы двух треугольников равны, то треугольники являются сходственными.
Важно отметить, что сходственные треугольники могут быть разных размеров, но сохраняют подобие своих сторон и углов. Это свойство позволяет схематически отображать сложные геометрические объекты в уменьшенном масштабе, сохраняя пропорции.
Сходственные треугольники используются в различных областях математики и геометрии, включая расчеты пропорций, построение подобных фигур, а также в рассмотрении и доказательстве геометрических теорем.
Условия сходственности треугольников
Треугольники называются сходственными, если у них соответственно равны все углы или все стороны, или все углы одного треугольника равны соответственно всем углам другого треугольника.
Для того чтобы два треугольника были сходственными, нужно проверить выполнение условий:
- Углы одних треугольников равны соответственно углам других треугольников.
- Стороны одних треугольников пропорциональны соответственно сторонам других треугольников.
- Если два треугольника имеют равные соответственно углы или стороны, то они сходственны.
Сходственные треугольники имеют много общих свойств и они могут быть использованы в решении различных задач, связанных с геометрией и тригонометрией. Они также играют важную роль при построении подобных фигур и определении соотношений между их сторонами и углами.
Как использовать сходственные треугольники в геометрии?
1. Решение подобных задач
Одним из основных применений сходственных треугольников является решение задач, связанных с подобием треугольников. Зная, что треугольники сходственные, можно использовать соответствующие свойства и соотношения для решения различных задач.
2. Нахождение пропорциональных отрезков
Еще одним способом использования сходственных треугольников является нахождение пропорциональных отрезков. При условии, что треугольники сходственные, можно использовать свойства подобия для нахождения отношений длин сторон и расстояний в треугольниках.
Все эти методы использования сходственных треугольников могут быть полезны в решении различных геометрических задач и построении точных и представительных моделей.
Простейшие свойства сходственных треугольников
Основные свойства сходственных треугольников:
- Углы треугольников сходственны, то есть соответствующие углы треугольников равны.
- Соответствующие стороны треугольников пропорциональны, то есть отношения длин соответствующих сторон равны.
- Сходственные треугольники имеют равные отношения площадей.
Сходственные треугольники имеют много применений в геометрии и решении задач. Например, с помощью сходственных треугольников можно вычислять расстояния и высоты, а также решать задачи по подобию фигур.
Разбираясь в свойствах и применении сходственных треугольников, можно улучшить свои навыки решения геометрических задач и расширить свои знания в данной области.
Примеры сходственных и несходственных треугольников
Сходственными треугольниками называются треугольники, у которых соответствующие стороны пропорциональны. То есть, если выполняется условие, что отношение длин одной стороны первого треугольника к длине соответствующей стороны второго треугольника равно отношению длин других сторон этих треугольников, то эти треугольники сходственны.
Несходственными треугольниками являются треугольники, у которых не выполняется условие пропорциональности сторон.
Пример 1: Сходственные треугольники
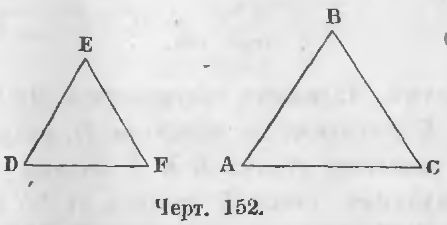
Рассмотрим треугольники ABC и DEF. Пусть AB/DE = BC/EF = AC/DF, то есть длины сторон соотносятся попарно. Треугольники ABC и DEF будут сходственными.
Пример 2: Несходственные треугольники
Рассмотрим треугольники PQR и XYZ. Пусть PQ/XY = QR/YZ, но PR/XZ ≠ 1/2, то есть одно из отношений длин сторон треугольников не совпадает. Треугольники PQR и XYZ будут несходственными.
Сходственность треугольников и теорема Менелая
Теорема Менелая — это одна из основных теорем, связанных с сходственными треугольниками. Суть теоремы состоит в том, что если из точки проведены три отрезка, пересекающих стороны треугольника, то произведение отношений длин отрезков, прилегающих к одной и той же стороне треугольника, равно единице. Формулировка теоремы Менелая несколько сложнее, но ее главное значение заключается в том, что она позволяет находить отношения длин сторон треугольника при условии, что проведены пересекающие отрезки.
Теорема Менелая имеет множество применений в различных областях геометрии, включая треугольники, окружности и многоугольники. Она используется для решения задач на подобие треугольников, нахождения отношений длин сторон, а также для доказательства других геометрических теорем.
Таким образом, знание о сходственности треугольников и теореме Менелая является важным компонентом геометрической подготовки и широко применяется в решении задач с участием треугольников и других геометрических фигур.
Вопрос-ответ:
Что такое сходственные треугольники?
Сходственные треугольники — это треугольники, у которых соответствующие углы равны, а соотношение длин их сторон постоянно. Они имеют одинаковую форму, но различаются в размерах.
Как определить, что треугольники сходственны?
Для того чтобы треугольники были сходственными, необходимо, чтобы все их внутренние углы были равны и стороны были пропорциональны. То есть, если соотношение длин сторон одного треугольника равно соотношению длин сторон другого треугольника, то они сходственны.
Какие свойства имеют сходственные треугольники?
У сходственных треугольников сохраняются следующие свойства: соответствующие углы равны, длины соответствующих сторон пропорциональны и соответствующие стороны пропорционально соединяют соответствующие углы.
Какая формула позволяет вычислить пропорциональность длин сторон сходственных треугольников?
Формула для вычисления пропорциональности длин сторон сходственных треугольников называется теоремой подобия треугольников. Она гласит, что соотношение длин сторон двух сходственных треугольников равно соотношению длин соответствующих сторон.