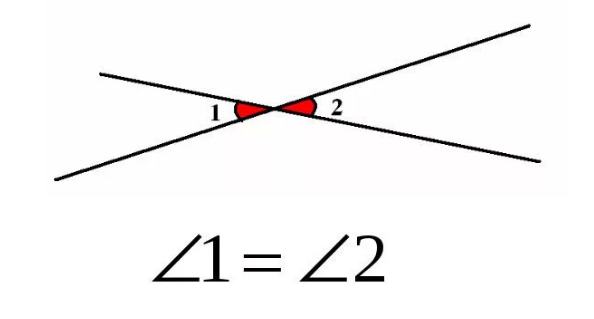
В математике и геометрии, вертикальные углы — это пары углов, которые образуются при пересечении двух прямых линий. Они обладают рядом особенных свойств и широко используются в различных задачах и теоремах.
Самое главное свойство вертикальных углов — они равны между собой. То есть, если две прямые линии пересекаются, образуя вертикальные углы, то каждый из углов будет иметь одинаковую меру. Это означает, что углы A и B равны между собой, а углы C и D также равны.
Вертикальные углы имеют широкое применение в решении различных геометрических задач и доказательств теорем. Например, они часто используются при доказательствах теорем о параллельных линиях, таких как теорема о внутренних углах, теорема о параллельных прямых и др.
Пример использования вертикальных углов: предположим, что у нас есть две перпендикулярные прямые линии, и мы хотим найти значение одного из вертикальных углов. Мы знаем, что вертикальные углы равны между собой, поэтому, если мы знаем значение одного из углов, мы можем найти значение другого угла.
Вертикальные углы
Такие углы образуются при пересечении двух прямых. Одна прямая будет вертикальна, а другая — наклонная. Углы, образованные этими прямыми, называются вертикальными углами.
Свойство вертикальных углов имеет практическое применение в геометрии и физике. Например, в процессе измерения различных углов, знание о равенстве вертикальных углов позволяет упростить вычисления.
Давайте рассмотрим несколько примеров использования вертикальных углов:
- При построении и измерении углов вождения автомобиля. Знание о вертикальных углах позволяет эффективно выравнивать колеса автомобиля и управлять его движением.
- В архитектуре. При проектировании зданий и сооружений используется понятие вертикальных углов для создания прямых и симметричных форм.
- В физике. Знание о равенстве вертикальных углов используется при измерении углов наклона и направления силы тяжести.
- В аэронавтике. При планировании полетов, расчете траекторий и навигации также применяется понятие вертикальных углов.
Вертикальные углы играют важную роль в различных областях науки и практических деятельностях. Знание и понимание этого свойства позволяет проще и точнее работать с углами и прямыми линиями.
Определение вертикальных углов
Основное свойство вертикальных углов заключается в их равенстве. Если два угла являются вертикальными, то они равны между собой. Это означает, что мера одного угла будет равна мере другого угла.
Пример использования вертикальных углов может быть найден в геометрии. Например, при решении задач, связанных с построением графиков функций, углы могут быть вертикальными, что позволяет нам найти измерение другого угла, исходя из известной величины.
| Пример | Измерение углов |
 |
|
Вертикальные углы могут быть полезны при решении геометрических задач, а также при проведении исследований в различных научных областях. Их свойства и применение имеют широкую область применения и являются важными понятиями в математике и науке в целом.
Что такое вертикальные углы?
Основное свойство вертикальных углов заключается в их равенстве. Если две прямые пересекаются, то все вертикальные углы, образующиеся между ними, имеют одинаковые значения. То есть, если угол №1 равен углу №2, то угол №3 будет равен углу №4.
Примеры использования вертикальных углов можно наблюдать в геометрии и в повседневной жизни. Например, при решении задач на построение чертежей или при определении плоскостей, применяются свойства вертикальных углов. Также, они могут быть полезны при анализе угловых отношений при сооружении зданий, дизайне интерьеров или при разработке компьютерных графики.
Изучение вертикальных углов помогает понимать и анализировать пространственные отношения и геометрические фигуры, а также применять этот навык в практических ситуациях.
Свойства вертикальных углов
Одним из основных свойств вертикальных углов является то, что их меры равны. Если две прямые линии пересекаются и образуют вертикальные углы, то каждый из этих углов имеет одинаковую меру. Это можно использовать, например, для доказательства двух углов равными в задачах на геометрию.
Еще одним свойством вертикальных углов является то, что они дополняют друг друга до 180 градусов. Если две вертикальные углы образуют пару, то их сумма равна 180 градусов. Это свойство можно использовать, чтобы находить меру одного угла, зная меру другого угла в задачах на геометрическую закономерность.
Также, вертикальные углы являются симметричными друг другу относительно пересекающихся прямых. Это означает, что если две прямые линии пересекаются и образуют вертикальные углы, то эти углы могут быть отражены друг относительно друга. Это свойство можно использовать для доказательства равенства углов в задачах на геометрию.
Использование свойств вертикальных углов позволяет решать геометрические задачи более эффективно и доказывать геометрические утверждения. Эти свойства обеспечивают основы для дальнейшего изучения геометрии и формирования логического мышления.
Примеры использования вертикальных углов
- Архитектура: При проектировании зданий инженерам и архитекторам необходимо учитывать вертикальные углы, чтобы создать прочные и эстетически приятные конструкции. Знание этих углов позволяет определить наклон стен и перекрытий, а также размещение окон и дверей.
- Дизайн интерьера: Вертикальные углы играют важную роль при планировании интерьера. Они определяют, какие предметы мебели можно разместить симметрично относительно стен или других вертикальных осей. Это может быть полезно при организации пространства в гостиной, спальне или офисе.
- Строительство: Вертикальные углы используются при проведении строительных работ. Они помогают рабочим правильно выставить стены или колонны, обеспечивая правильный наклон и устойчивость конструкций. Кроме того, знание вертикальных углов важно при проведении загородных работ, таких как возведение забора или установка опор для электрической линии.
- Геодезия: Вертикальные углы широко используются в геодезии — науке о измерениях и картографии. Они помогают определить вертикальное положение точек на местности и создать высотные карты. Это важно при строительстве дорог, мостов, а также при проведении гидрографических и геологических исследований.
- Навигация: Вертикальные углы играют роль в навигации, особенно в авиации и мореплавании. Они используются для определения вертикального наклона самолета или судна, а также для обеспечения безопасного подъема или спуска. Это особенно важно при посадке или взлете на аэродроме.
Это лишь несколько примеров, как вертикальные углы используются в различных областях. Понимание этого свойства является важным для решения различных задач и обеспечения качественного выполнения работ.
Применение вертикальных углов в геометрии
Вертикальные углы имеют равные величины, то есть, если две линии пересекаются, то соответствующие вертикальные углы равны между собой. Это свойство можно использовать для решения задач на поиск неизвестных углов.
Например, если дана геометрическая фигура с пересекающимися линиями и известны величины нескольких вертикальных углов, можно использовать их равенство, чтобы найти величину других неизвестных углов. Также вертикальные углы могут быть использованы для доказательства равенства двух углов в геометрическом построении.
Для более наглядного представления вертикальных углов и их равенств можно использовать таблицу. Ниже приведен пример таблицы, в которой указаны значения неизвестных углов, найденные с использованием свойства вертикальных углов.
| Угол | Значение |
|---|---|
| 1 | 60° |
| 2 | 120° |
| 3 | 60° |
| 4 | 120° |
Таким образом, использование вертикальных углов в геометрии позволяет найти значения неизвестных углов и доказывать равенство углов в различных геометрических построениях.
Вопрос-ответ:
Что такое вертикальные углы?
Вертикальные углы — это пары углов, расположенных напротив друг друга при пересечении двух прямых линий. Такие углы имеют равные значения.
Как можно определить вертикальные углы?
Чтобы определить вертикальные углы, необходимо найти две пересекающиеся прямые линии и обратить внимание на углы, которые расположены напротив друг друга.
Какое свойство у вертикальных углов?
Свойство вертикальных углов заключается в том, что они имеют равные значения. Если один из вертикальных углов равен, например, 60 градусам, то и другой вертикальный угол будет равен 60 градусам.
Как использовать вертикальные углы в геометрии?
Вертикальные углы используются в геометрии для решения различных задач и построений. Например, зная значение одного из вертикальных углов, можно найти значение другого вертикального угла, так как они равны. Также, зная значение вертикального угла, можно определить значения других углов, таких как смежные углы или углы, образованные двумя пересекающимися прямыми линиями.
Приведите примеры использования вертикальных углов в повседневной жизни.
В повседневной жизни вертикальные углы могут использоваться, например, при построении мебели. Зная значения вертикальных углов, можно правильно выставить направление и наклон элементов мебели, чтобы они были симметричными и углы между ними были равными. Также, знание вертикальных углов может быть полезно при выполнении строительных работ, чтобы правильно выставить вертикальные стены или балки.
Что такое вертикальные углы?
Вертикальные углы — это пара углов, которые находятся напротив друг друга и имеют равные меры. То есть, если один угол равен, например, 45 градусов, то его вертикальный угол (расположенный напротив него) тоже будет равен 45 градусам. Вертикальные углы образуются при пересечении двух прямых линий.
Каково свойство вертикальных углов?
Основным свойством вертикальных углов является их равенство. Если две прямые линии пересекаются, то вертикальные углы, образованные этим пересечением, будут равны между собой. Это свойство можно использовать для решения различных задач, например, для нахождения неизвестных углов при известных значениях других углов, а также для доказательства равенства углов в геометрических конструкциях.