
Высотой треугольника называется отрезок, проведенный из вершины треугольника к противоположной стороне и перпендикулярный ей. Она является одной из важнейших характеристик треугольника и позволяет определить его площадь.
Высоту треугольника обозначают буквой h и она может быть проведена для каждой из трех сторон треугольника. Если треугольник имеет особые свойства, например, прямоугольный или равнобедренный, то высота будет иметь определенное значение.
Для прямоугольного треугольника, высота, проведенная к гипотенузе, будет равна произведению катета, стоящего на пути этой высоты, на катет, лежащий весьма на пути этой высоты. Высота, проведенная из вершины прямого угла, будет равна величине другой катета.
Что такое высота треугольника?
Высотой треугольника называют перпендикуляр, опущенный из одного из вершин треугольника к противоположной стороне или её продолжению. Таким образом, высота треугольника представляет собой отрезок, соединяющий вершину треугольника с основанием, проходящим через противоположную сторону или её продолжение.
Высота представляет собой важный элемент треугольника, так как она позволяет определить площадь фигуры и находить другие характеристики треугольника. Высота треугольника разделяет фигуру на два прямоугольных треугольника и служит основой для формулы нахождения площади треугольника.
Высота треугольника может быть внутренней или внешней. Внутренняя высота проходит через вершину треугольника и перпендикулярна основанию, расположенному на противоположной стороне. Внешняя высота также проходит через вершину, но продолжается за пределы треугольника и пересекает основание.
Помните, что высота треугольника зависит от выбора вершины и стороны, относительно которой строится перпендикуляр. Один треугольник может иметь несколько высот, и каждая из них будет отличаться.
Зная высоту треугольника, мы можем использовать её для вычисления площади фигуры. Формула для вычисления площади треугольника при известной высоте:
S = (основание * высота) / 2
Высота треугольника является важным понятием в геометрии, и её понимание позволяет более полно описывать и анализировать треугольники и их свойства.
Высота треугольника: определение и свойства
Основные свойства высоты треугольника:
- Высота всегда перпендикулярна к основанию треугольника.
- Высота является самым коротким расстоянием от вершины треугольника до основания.
- В треугольнике можно провести три высоты, каждая из которых будет соединять вершину с одной из сторон треугольника.
- Точка пересечения высот с основанием называется основанием перпендикуляра.
- Высоты треугольника могут быть внутренними и внешними, в зависимости от того, находятся ли они внутри треугольника или за его пределами.
Знание высоты треугольника и свойств, связанных с ней, позволяет решать различные задачи и вычисления, связанные с треугольниками в геометрии.
Как найти высоту треугольника?
Существует несколько способов найти высоту треугольника:
1. По формуле
Если известны длины сторон треугольника, то высоту можно найти, используя формулу:
h = 2 * (Площадь треугольника) / (Длина основания)
где h — высота треугольника, а Площадь треугольника рассчитывается по формуле Герона.
Например, для прямоугольного треугольника, где одна из сторон является основанием, высоту можно найти, зная длины катетов.
2. По теореме Пифагора
Если треугольник является прямоугольным, то его высота, проведенная к гипотенузе, равна произведению катета на расстояние от основания до точки пересечения высоты с гипотенузой.
То есть, если a и b — катеты треугольника, а c — гипотенуза, то высоту можно найти по формуле:
h = (a * b) / c
Формула для вычисления высоты треугольника
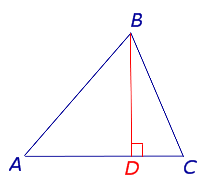
Формула для вычисления высоты треугольника
Существует несколько способов вычисления высоты треугольника в зависимости от доступных данных. Один из наиболее простых способов — использование основания треугольника и его высоты.
Формула для вычисления высоты треугольника:
h = (2 * S) / a
где:
- h — высота треугольника;
- S — площадь треугольника;
- a — основание треугольника.
Для использования данной формулы необходимо знать площадь треугольника и длину его основания. Если площадь треугольника неизвестна, ее можно вычислить, используя формулу для площади треугольника.
Пример применения формулы
Рассмотрим пример. Пусть у нас есть треугольник со сторонами длиной 5, 12 и 13 единиц. Чтобы вычислить высоту треугольника, сначала найдем площадь треугольника:
S = (a * b) / 2 = (5 * 12) / 2 = 30
Затем, подставим значения площади и основания в формулу:
h = (2 * 30) / 5 = 12
Таким образом, высота треугольника равна 12 единицам.
Формула для вычисления высоты треугольника позволяет узнать данную характеристику геометрической фигуры и использовать ее для решения задач в различных областях науки и техники.
Первый способ
Один из способов вычисления высоты треугольника основан на формуле:
Высота треугольника равна произведению длины основания на соответствующую ему высоту, разделенное на два:
h = (a * ha) / 2
Где:
- h — высота треугольника;
- a — длина основания;
- ha — соответствующая основанию высота.
Этот способ особенно удобен, когда известны значения основания и соответствующей высоты треугольника. Применяя данную формулу, можно легко и быстро определить высоту треугольника, зная значения этих двух параметров.
Второй способ
Второй способ нахождения высоты треугольника основан на использовании формулы Герона. Для этого требуется знать длины всех сторон треугольника.
Формула Герона позволяет найти площадь треугольника по его сторонам. Пусть a, b и c — длины сторон треугольника, а p — полупериметр треугольника (сумма длин всех сторон, делённая на 2).
Площадь треугольника можно найти по формуле:
S = √(p * (p — a) * (p — b) * (p — c))
Высота треугольника, опущенная на сторону a, равна:
ha = (2 * S) / a
Аналогично, можно найти высоты треугольника, опущенные на остальные стороны.
Значение высоты треугольника в геометрии
Значение высоты треугольника заключается в том, что она служит основой для нахождения площади треугольника по формуле «площадь = 0,5 * основание * высота». Также высота треугольника используется для нахождения длины его сторон по теореме Пифагора и другим геометрическим методам.
Высота треугольника может быть найдена с помощью различных методов, в зависимости от известных данных о треугольнике. Например, если известны длины сторон треугольника, то высоту можно найти с помощью формулы герона или теоремы Герона. Если известны координаты вершин треугольника, то высоту можно найти с помощью формулы для расстояния между двумя точками в пространстве.
Высота треугольника имеет также важное значение при решении геометрических задач. Она позволяет находить различные параметры треугольника, такие как углы, стороны, площадь, периметр и другие. Высота также используется при нахождении центра тяжести треугольника и построении медиан и ортоцентра.
Таким образом, значение высоты треугольника в геометрии является важным и полезным понятием, которое используется для нахождения различных параметров треугольника и решения геометрических задач.
Применение высоты треугольника в практике
Геометрия:
В геометрии высота треугольника определяется как отрезок, соединяющий вершину треугольника с противоположной стороной. Высоты треугольника обладают рядом важных свойств и связей. Они позволяют находить площадь треугольника, вписанных в него окружностей, проводить перпендикуляры и многое другое.
Архитектура и строительство:
Высота треугольника расширяет возможности в области архитектуры и строительства. Она позволяет разрабатывать и строить различные конструкции, включая пирамиды, здания, мосты и другие сооружения. Зная высоты треугольника, можно проводить расчеты и проектировать строительные объекты с учетом их графического изображения.
Геодезия и картография:
Высоты треугольника применяются в геодезии и картографии для определения высот и создания топографических карт. С помощью специальных приборов и методов измерения, высоты треугольника используются для определения географических координат объектов, создания трехмерных моделей местности и прочих геодезических работ.
Физика и инженерия:
Высоты треугольника играют важную роль в физике и инженерии. Они используются, например, для определения высоты объектов или местности, измерения расстояний и прочих физических параметров. Высоты треугольника применяются также для решения задач в механике, электротехнике, теплотехнике и других областях техники и науки.
Высота треугольника играет важную роль в практических и научных задачах, связанных с геометрией, архитектурой, геодезией, физикой и др. Понимание и применение высоты треугольника помогает строить точные расчеты, проводить качественные измерения и создавать надежные конструкции.
Вопрос-ответ:
Что такое высота треугольника?
Высотой треугольника называют линию, которая проходит через вершину треугольника и перпендикулярна одной из сторон или ее продолжению.
Как найти высоту треугольника?
Высоту треугольника можно найти разными способами, в зависимости от известных данных. Один из способов — использовать формулу для нахождения площади треугольника: высота равна произведению длины одной из сторон треугольника на два, разделенное на длину противолежащей этой стороне высоты. Также высоту можно найти, используя теорему Пифагора или треугольники подобия.
Зачем нужна высота треугольника?
Высота треугольника используется для различных расчетов и построений. Например, она позволяет найти площадь треугольника, определить его прямоугольность, найти длины других сторон и углов треугольника, а также решить некоторые геометрические задачи.
Сколько высот может быть у треугольника?
У треугольника может быть три высоты, которые соответствуют каждой из его сторон. Высоты треугольника не могут быть параллельными или совпадающими, они пересекаются в одной точке, называемой ортоцентром.