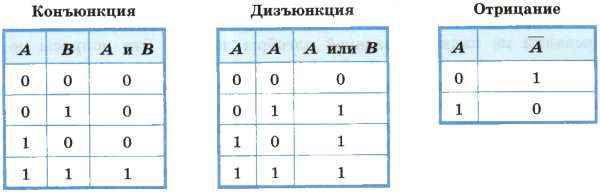
Одной из основных операций в логике является дизъюнкция. Она позволяет объединять два высказывания в одно, утверждая, что хотя бы одно из них истинно. Однако есть еще одно название для этой операции, которое меньше известно широкому кругу людей.
Дизъюнкция также называется логическим ИЛИ, поскольку она действует подобно естественному языковому союзу «или». В английском языке для этого используется союз «or». Таким образом, операция дизъюнкции позволяет нам выражать альтернативу в наших высказываниях.
Например, можно использовать дизъюнкцию, чтобы объединить два высказывания: «Солнце светит» и «Идет дождь». Если мы скажем «Солнце светит или идет дождь», то это означает, что хотя бы одно из этих высказываний истинно. Если на улице идет дождь, второе высказывание будет истинным, в то время как первое высказывание будет ложным, и наоборот.
Что такое дизъюнкция?
Дизъюнкция может быть представлена в виде символа «V» или «+».
Операция дизъюнкции выполняет следующие правила:
Правило сложения

Если хотя бы одно из утверждений верно, то дизъюнкция будет верной. Например, если у нас есть утверждения «Сегодня идет дождь» и «Сегодня светит солнце», то их дизъюнкция будет истинной, так как хотя бы одно из утверждений верно.
Правило исключения третьего
Если у нас есть утверждение «Сегодня идет дождь» и «Сегодня не идет дождь», то их дизъюнкция будет истинной, так как хотя бы одно из утверждений верно. Это правило основано на том, что нет третьего варианта: либо дождь идет, либо не идет.
Операция дизъюнкции может быть применена не только к простым утверждениям, но и к комплексным выражениям. Результатом дизъюнкции всегда будет либо истинное, либо ложное значение.
Дефиниция дизъюнкции
Обозначается дизъюнкция символами «или», «∨» или «+». Например, высказывание «Сегодня идет дождь или ты не прав» является дизъюнкцией двух простых высказываний.
Для понимания дизъюнкции необходимо учитывать ее истинностную таблицу. Если оба высказывания, объединенные дизъюнкцией, ложны, то сама дизъюнкция также ложна. Во всех остальных случаях, когда хотя бы одно из высказываний истинно, дизъюнкция будет истинна.
Операции с дизъюнкцией
Операции над двумя переменными
Дизъюнкция может быть применена к двум логическим переменным. Результат операции будет истинным, если хотя бы одна из переменных истинна. В противном случае, если обе переменные ложны, результат будет ложным.
Например, для двух переменных A и B, дизъюнкция A+ B будет истинной, если A или B истинны, и ложной, только если и A, и B ложны.
Таблица истинности для операции дизъюнкции представлена ниже:
| A | B | A + B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Дополнительные свойства операции
Операция дизъюнкции обладает несколькими важными свойствами:
- Коммутативность: Порядок операндов не влияет на результат. То есть A+ B = B+ A.
- Ассоциативность: Порядок выполнения операции не влияет на результат при наличии более двух операндов. То есть (A+ B)+ C = A+ (B+ C).
- Идемпотентность: Если операнд повторяется, результат не изменяется. То есть A+ A = A.
Операция дизъюнкции широко используется в логических выражениях и вычислительных системах для принятия решений на основе логических условий.
Символы дизъюнкции
Символ «+»
Один из наиболее распространенных символов для обозначения дизъюнкции является символ «+». Например, высказывание «А + В» означает, что выполнено либо условие А, либо условие В, или оба сразу.
Символ «∨»
Также дизъюнкцию можно обозначить символом «∨», который является символом логического «ИЛИ». Например, высказывание «А ∨ В» имеет тот же смысл, что и высказывание «А + В», то есть выполняется одно из условий или оба сразу.
Использование символов дизъюнкции помогает логике и математике обозначать операцию объединения двух или более высказываний, что является важным инструментом при решении различных задач и построении логических моделей.
Дизъюнкция в математике
При использовании дизъюнкции образуется новое высказывание, которое является истинным, если хотя бы одно из исходных высказываний истинно. Например, для высказываний «Сегодня солнечный день» и «Сегодня дождь» дизъюнкцией будет являться высказывание «Сегодня солнечный день или дождь».
Дизъюнкция имеет следующие правила:
— Если хотя бы одно из исходных высказываний истинно, то и дизъюнкция истинна.
— Если все исходные высказывания ложны, то и дизъюнкция ложна.
— Порядок вычисления дизъюнкции не имеет значения, ассоциативность операции позволяет группировать выражения различными способами.
Дизъюнкция широко используется в математической логике, а также в программировании для задания условий или проверки различных вариантов. Она является основной операцией в логическом вычислении и обладает рядом свойств, которые позволяют более точно определить истинность выражений.
Дизъюнкция в логике
Дизъюнкция является одной из основных операций в логике и широко используется для построения сложных высказываний. Она имеет следующие свойства:
Свойства дизъюнкции
- Коммутативность: порядок высказываний не влияет на результат дизъюнкции. То есть A или B равносильно B или A.
- Ассоциативность: при наличии трех или более высказываний, результат дизъюнкции не зависит от способа их расстановки. То есть (A или B) или C равносильно A или (B или C).
- Распределительность: дизъюнкция можно распределить относительно других операций. Например, A и (B или C) равносильно (A и B) или (A и C).
- Идемпотентность: повторение одного и того же высказывания в дизъюнкции не меняет ее значения. То есть A или A равносильно A.
- Истина: если хотя бы одно из высказываний в дизъюнкции истинно, то результат дизъюнкции также истинен.
- Ложь: только в том случае, когда все высказывания в дизъюнкции ложны, результат дизъюнкции будет ложным.
Другие названия дизъюнкции
Операция дизъюнкции, также известная как логическое «или», имеет несколько других названий:
1. «Логическое сложение»
2. «Логическая дизъюнкция»
3. «Инклюзивное или»
4. «Альтернативное или»
Логическое сложение
В математической логике дизъюнкция выполняет операцию сложения для логических значений. Она возвращает «истина» только в том случае, когда хотя бы одно из входных значений равно «истина».
Инклюзивное или
Термин «инклюзивное или» подчеркивает, что операция дизъюнкции включает оба входных значения. Если оба значения равны «истина», результат также будет «истиной». Это отличает инклюзивное или от исключающего или, которое возвращает «истину» только в том случае, когда одно из значений равно «истина».
Итак, операция дизъюнкции имеет несколько названий, но все они описывают одну и ту же основную идею — выбор одного из нескольких вариантов. Знание этих терминов позволяет лучше понимать логические операции и их применение в различных областях.
Вопрос-ответ:
Что такое операция дизъюнкция и как она называется?
Операция дизъюнкция в логике и математике является одной из основных бинарных операций, которая выводит истинное значение, если хотя бы один из ее операндов истинен. Также дизъюнкцию можно назвать «логическим ИЛИ».
Для чего используется операция дизъюнкция?
Операция дизъюнкция используется в логических выражениях и математических операциях для объединения условий или значений. Она позволяет проверить, выполняется ли хотя бы одно из условий, и в зависимости от результата сделать определенное действие.
Каким символом обозначается операция дизъюнкция?
Обычно операция дизъюнкция обозначается символом «∨» или символом «+».
В каких областях знаний используется операция дизъюнкция?
Операция дизъюнкция используется в логике, математике, программировании, электронике, физике и других областях знаний, где требуется логическое объединение условий, значений или событий.
Какие свойства имеет операция дизъюнкция?
Операция дизъюнкция обладает несколькими свойствами, такими как коммутативность, ассоциативность, дистрибутивность, идемпотентность и нейтральность. Эти свойства позволяют выполнять логические операции и преобразовывать логические выражения с помощью дизъюнкции.
Как называется операция дизъюнкция?
Операция дизъюнкция также называется логическим ИЛИ.