
В геометрии существует несколько видов фигур, и, конечно же, они бывают разных размеров и форм. Однако существует понятие равных фигур, которые при всех отношениях и свойствах остаются одинаковыми. Но какие именно фигуры считаются равными и как это определяется?
Во-первых, равные фигуры должны иметь одинаковую форму. Это значит, что все углы и стороны этих фигур должны быть равны друг другу. Например, если у двух прямоугольников все углы и стороны равны, то эти две фигуры считаются равными.
Во-вторых, равные фигуры должны иметь одинаковую площадь. Это значит, что если взять равную долю одной фигуры и попытаться полностью ее заполнить другой фигурой, то это должно быть возможно. И наоборот, если разделить равномерно две фигуры и получить идентичные кусочки у обоих, то эти фигуры являются равными.
Также равные фигуры должны иметь одинаковый объем в пространстве. Например, если взять два параллелепипеда и в один из них полностью уместить объем другого, то эти фигуры считаются равными. Однако объем может быть сложнее проверить, чем площадь, так как требует использования формул и расчетов.
Что такое равные фигуры?
Равные фигуры обладают рядом важных свойств:
- Форма: равные фигуры имеют одинаковую форму, то есть их геометрические контуры совпадают.
- Размеры: равные фигуры имеют одинаковые линейные размеры, такие как длина сторон, радиусы, диаметры и углы.
- Положение: равные фигуры могут быть совмещены друг с другом так, чтобы совпадать во всех точках. При совмещении фигур не должно быть искажений, поворотов или переворотов, только параллельное перемещение.
Равные фигуры являются основным понятием в геометрии и имеют важное значение при решении различных задач и построении различных фигур.
Какие критерии определяют равные фигуры?
Для определения равенства фигур необходимо выполнение следующих критериев:
- Критерий соответствия формы — фигуры считаются равными, если все их углы и стороны соответствуют друг другу. То есть, если у этих фигур одни и те же углы и стороны, они считаются равными, независимо от их положения в пространстве.
- Критерий равенства размеров — фигуры считаются равными, если все их размеры, такие как радиусы, длины сторон или высоты соответствуют друг другу. Если все размеры одной фигуры равны соответствующим размерам другой фигуры, то они считаются равными.
- Критерий равенства объема — в случае трехмерных фигур, равными считаются те фигуры, объемы которых одинаковы. Если объемы двух фигур равны, то эти фигуры считаются равными.
При определении равенства фигур важно учитывать все указанные критерии. Если фигуры удовлетворяют всем условиям, то можно с уверенностью сказать, что они равны. И наоборот, если хотя бы одно условие не выполняется, фигуры не считаются равными.
Примеры равных фигур в пространстве
— Кубы: два куба с равными длинами ребер, углами и площадью граней будут равными.
— Цилиндры: два цилиндра с равными радиусами оснований и высотами будут равными.
— Параллелепипеды: два параллелепипеда с равными площадями оснований и высотами будут равными.
— Пирамиды: две пирамиды с равными основаниями и высотами будут равными.
— Шары: два шара с равными радиусами будут равными.
— Конусы: два конуса с равными радиусами оснований и высотами будут равными.
Это лишь некоторые примеры равных фигур в пространстве. В геометрии очень важно понимать понятие равенства фигур, так как оно используется при решении различных задач и доказательств теорем.
Какими свойствами обладают равные фигуры?
Равные фигуры обладают рядом характерных свойств, которые позволяют определить их равенство.
1. Равенство величины
Равные фигуры имеют одинаковую площадь или объем. Это значит, что все их соответствующие стороны, углы и диагонали равны между собой.
2. Геометрическая конгруэнтность
Равные фигуры геометрически конгруэнтны, то есть совпадают друг с другом при некотором преобразовании: параллельном переносе, повороте или отражении. Это значит, что при совмещении одной фигуры с другой с помощью этих преобразований они в точности совпадут.
Таким образом, равные фигуры обладают идентичной формой и размерами, что позволяет нам утверждать их равенство.
Какие проблемы могут возникнуть при определении равных фигур?
При определении равных фигур в пространстве могут возникнуть ряд проблем, которые требуют внимательного анализа и конкретных критериев для их решения. Вот некоторые из них:
1. Определение точности измерений

Определение равенства фигур в пространстве может потребовать точных измерений, особенно если они имеют сложную форму или содержат несколько элементов. Точность измерений может зависеть от используемого инструмента и методики измерения, поэтому необходимо учитывать возможные погрешности и их влияние на результат.
2. Учет ориентации и положения фигур
Определение равенства фигур включает не только сравнение их формы и размеров, но также учет их ориентации и положения в пространстве. Две фигуры могут иметь одинаковую форму и размеры, но иметь разные ориентации. Для установления равенства необходимо учесть и сравнить их положение и ориентацию.
3. Учет внутренней структуры фигур
Равные фигуры могут иметь различную внутреннюю структуру, что может затруднить их сравнение. Например, два тетраэдра могут иметь одинаковую форму и внешние размеры, но иметь разную внутреннюю структуру, если их грани или вершины отличаются. При сравнении фигур необходимо учитывать их внутреннюю структуру, чтобы определить равны ли они.
4. Приближенные значения и округления
При работе с физическими объектами и измерениями возникает необходимость округлять значения и использовать приближенные числа. Округление и приближение значений могут привести к незначительным изменениям формы или размеров фигур, что может усложнить задачу определения их равенства. При сравнении фигур необходимо учитывать возможные округления и приближения, чтобы не допустить ошибок в результате.
Все эти проблемы требуют внимательного анализа и оценки для достижения правильного определения равенства фигур в пространстве. Их решение заключается в определении конкретных критериев и методик сравнения, которые учитывают все особенности и требования данной задачи.
Методы проверки равенства фигур
В геометрии существует несколько методов проверки равенства фигур, которые позволяют определить, совпадают ли они друг с другом. Проверка равенства фигур играет важную роль в решении геометрических задач и построении различных конструкций.
Методы сравнения фигур по сторонам и углам
Например, чтобы убедиться в равенстве двух треугольников, необходимо сравнить длины их сторон и углы. Если все стороны и углы первого треугольника равны соответствующим сторонам и углам второго треугольника, то треугольники можно считать равными.
Методы сравнения фигур по площади и объему
Помимо сравнения сторон и углов, фигуры можно сравнивать и по их площади (в случае плоских фигур) или объему (в случае пространственных фигур). Если площади или объемы двух фигур равны, то можно считать, что они равны.
Однако, следует отметить, что равенство площадей или объемов фигур не всегда является достаточным условием их равенства. Например, у двух разных пятиугольников может быть одинаковая площадь, но при этом они не будут равными фигурами.
Важно отметить, что проверка равенства фигур может включать использование нескольких методов одновременно. Кроме того, существуют и другие методы проверки равенства фигур, которые не были указаны в данной статье.
Зачем нужно знать равные фигуры?
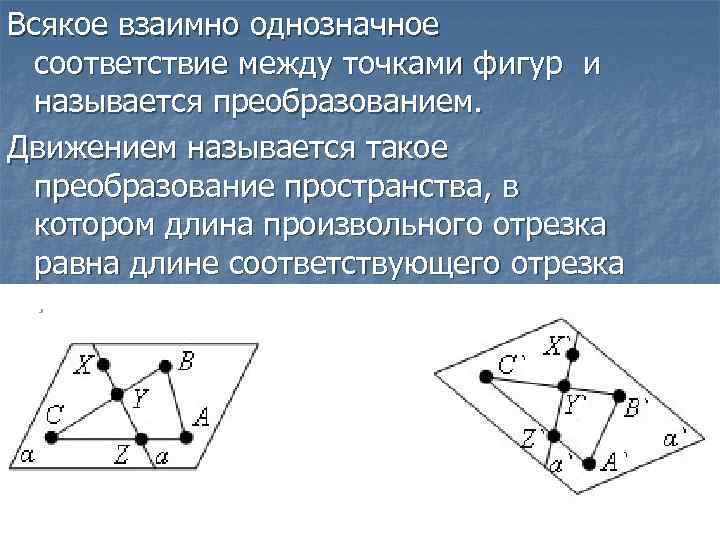
Равные фигуры: определение
Равные фигуры — это фигуры, у которых все соответствующие стороны и углы равны друг другу. Такие фигуры могут быть разного вида: треугольники, прямоугольники, круги и множество других. Важно помнить, что равные фигуры имеют одинаковую форму, но размеры могут быть разными.
Практическое применение равных фигур
Знание равных фигур позволяет нам:
- Решать геометрические задачи: зная, что две фигуры равны, мы можем использовать это знание для определения значений и свойств других сторон и углов.
- Повышать точность измерений: сравнивая фигуры, мы можем определить, являются ли они равными, что помогает нам измерять и сравнивать длины, площади, объемы и другие параметры.
- Разрабатывать новые способы конструирования: равные фигуры могут служить основой для создания новых фигур и структур.
Знание равных фигур является важной составляющей математического образования и способствует развитию аналитического мышления и логического рассуждения. Кроме того, умение работать с равными фигурами может быть полезно в различных профессиональных областях, таких как архитектура, инженерия и дизайн.
Вопрос-ответ:
Какие фигуры считаются равными в трехмерном пространстве?
В трехмерном пространстве фигуры считаются равными, если они имеют одинаковую форму и размеры. То есть, все их грани и углы должны быть одинаковыми. Например, два параллелепипеда с одинаковыми сторонами будут считаться равными.
Какими особенностями должны обладать фигуры, чтобы считаться равными в пространстве?
Чтобы фигуры считались равными в пространстве, они должны иметь одинаковую форму и одинаковые размеры. В дополнение к этому, все их грани, ребра и углы должны быть одинаковыми. Это означает, что они могут быть совмещены трехмерными пространственными преобразованиями, такими как повороты и сдвиги.
В чем разница между понятиями «равные фигуры» и «подобные фигуры» в пространстве?
Равные фигуры в пространстве имеют одинаковую форму и размеры, то есть они абсолютно идентичны друг другу и могут быть совмещены точно. Подобные фигуры, с другой стороны, имеют одинаковую форму, но могут иметь разные размеры. Они могут быть увеличены или уменьшены друг относительно друга с помощью пространственных преобразований.
Почему фигуры с одинаковыми размерами и формой считаются равными в пространстве?
Фигуры с одинаковыми размерами и формой считаются равными в пространстве, потому что все их грани, ребра и углы полностью совпадают друг с другом. Это значит, что одну фигуру можно точно совместить с другой, используя трехмерные пространственные преобразования, такие как повороты и сдвиги. В результате получается идентичное положение и форма.