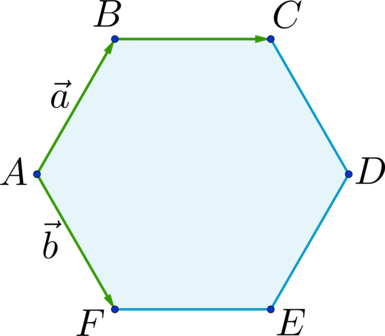
Правило сложения неколлинеарных векторов является одним из основных и важных понятий в линейной алгебре. Оно позволяет нам определить сумму двух или более векторов в трехмерном пространстве. Сложение векторов позволяет нам решать множество задач в физике, геометрии, механике и других областях науки и техники.
Неколлинеарные векторы — это векторы, которые не лежат на одной прямой. Коллинеарные векторы имеют одинаковые или противоположные направления, а неколлинеарные — разные направления. Когда мы складываем неколлинеарные векторы, мы получаем итоговый вектор, который является результатом суммы всех векторов.
Правило сложения неколлинеарных векторов можно представить следующим образом: если у нас есть два вектора A и B, мы можем сложить их, чтобы получить новый вектор C. Для этого мы просто берем начальную точку вектора A и проводим от нее линию, равную по направлению и величине вектора B. Точка, в которой пересекаются эти линии, и будет конечной точкой вектора C.
Правило сложения неколлинеарных векторов
Для сложения двух неколлинеарных векторов необходимо применить векторный метод, основанный на принципе параллелограмма. Пусть имеются два вектора а и б. Для получения вектора-суммы необходимо провести стрелки этих векторов из одной точки и затем построить параллелограмм с помощью этих стрелок. Вектор-сумма будет направлена от начала первого вектора до конца второго вектора.
Длина вектора-суммы определяется по модулю покомпонентным сложением длин векторов а и б. Его направление определяется посредством проведения диагонали параллелограмма, которая соединяет начало первого вектора с концом второго вектора.
Результатом сложения двух неколлинеарных векторов является новый вектор, который обладает свойствами своих составляющих векторов, но имеет другую ориентацию и модуль.
Правило сложения неколлинеарных векторов применяется во многих областях, включая физику, механику, геометрию и технические науки. Оно позволяет эффективно работать с векторными величинами и определять результат их суммы.
Понятие и основные принципы
Основные принципы сложения неколлинеарных векторов:
| № | Принцип | Объяснение |
|---|---|---|
| 1 | Компонентный подход | Векторы разлагаются на свои компоненты по координатным осям. Затем компоненты каждого вектора складываются по соответствующим осям. |
| 2 | Метод графической суммы | Векторы изображаются стрелками на координатной плоскости. Затем стрелки суммируются по правилу параллелограмма, где диагональ параллелограмма является искомой суммой векторов. |
| 3 | Метод треугольника | Векторы изображаются стрелками на координатной плоскости так, чтобы их начало совпало. Затем стрелки складываются по правилу треугольника, где искомый вектор является стороной треугольника. |
С общим пониманием этих принципов, можно успешно выполнять сложение неколлинеарных векторов и решать задачи, связанные с векторной алгеброй, механикой и физикой в целом.
Что такое неколлинеарные векторы
Два вектора называются неколлинеарными, если их линейная комбинация, то есть сумма или разность, не равна нулевому вектору. Если вектора имеют ненулевую линейную комбинацию, то они неколлинеарны и образуют плоскость.
Определение неколлинеарных векторов связано с понятием линейной независимости. Векторы называются линейно зависимыми, если один из векторов может быть представлен в виде линейной комбинации других векторов. Если нет такой комбинации, то векторы называются линейно независимыми и неколлинеарными.
Неколлинеарные векторы играют важную роль в математической физике и геометрии. Они используются для описания движения объектов, построения трехмерных моделей и нахождения решений в физических и инженерных задачах.
Основные свойства неколлинеарных векторов
1. Коммутативность:
Правило сложения векторов гласит, что для неколлинеарных векторов порядок слагаемых не имеет значения. То есть, если заданы два неколлинеарных вектора a и b, то a + b = b + a.
2. Ассоциативность:
Сложение векторов ассоциативно, что означает, что при сложении трех векторов a, b и c, результат не зависит от того, какие векторы размещены в скобках. То есть, (a + b) + c = a + (b + c).
3. Существование нейтрального элемента:
Для неколлинеарных векторов существует нулевой вектор 0, который при сложении с любым вектором не изменяет его. То есть, для любого вектора a выполняется a + 0 = a.
4. Обратный элемент:
Для каждого неколлинеарного вектора a существует вектор —a, который при сложении с a дает нулевой вектор. То есть, для любого вектора a существует вектор —a такой, что a + (-a) = 0.
5. Потенциальное исключение:
Неколлинеарные векторы не всегда возможно сложить. Если они направлены в противоположные стороны и имеют одинаковую длину, их сумма равна нулевому вектору. В этом случае говорят, что векторы компенсируют друг друга.
Правило сложения
Для выполнения правила сложения векторов нужно:
- Выбрать точку начала для первого вектора.
- Построить первый вектор на основании направления (угла) и его длины (модуля).
- Выбрать точку начала для второго вектора и построить его.
- Провести прямые векторов от их начал к их концам. Получившийся параллелограмм будет иметь диагональ, которая является суммой векторов.
- Отследить прямую от начальной точки первого вектора до конечной точки второго вектора. Полученная прямая и будет суммой векторов.
Результатом сложения векторов будет новый вектор, который будет представлять собой сумму их длин и иметь направление, соответствующее результату сложения.
Определение сложения векторов
Для векторов, которые не коллинеарны (не лежат на одной прямой), сложение осуществляется по правилу параллелограмма. Согласно этому правилу, результирующий вектор получается по диагонали параллелограмма, построенного на двух слагаемых векторах.
При сложении неколлинеарных векторов длина и направление результирующего вектора определяются с помощью векторной суммы. Векторная сумма векторов A и B обозначается как A + B.
В общем случае, сложение векторов может быть представлено в виде:
A + B = C
где A и B – слагаемые векторы, а C – результирующий вектор.
Операция сложения векторов широко используется в различных областях науки и инженерии, таких как механика, физика, информатика и т.д.
Примеры применения правила сложения
Правило сложения неколлинеарных векторов широко применяется в физике и геометрии для определения результирующего вектора при сложении нескольких векторов.
Например, при учете сил, действующих на тело, векторы сил могут быть сложены в соответствии с правилом сложения. Результирующий вектор будет представлять силу, действующую на тело.
Также векторное сложение векторов используется при определении направления и величины скорости движения объектов. Если известны векторы скорости отдельных объектов, их можно сложить для получения вектора скорости относительно некоторой точки.
Одним из простых примеров применения правила сложения является нахождение результирующего вектора при перемещении в пространстве. Если движение происходит с постоянной скоростью и в одном направлении, векторы перемещения могут быть сложены, чтобы получить вектор, указывающий на конечную точку.
Таким образом, правило сложения неколлинеарных векторов является важным инструментом в физике и геометрии, позволяющим определить результирующий вектор при сложении нескольких векторов.
Геометрическая интерпретация
Сложение неколлинеарных векторов выполняется следующим образом:
- Выбирается начальная точка первого вектора.
- Из этой точки проводится отрезок прямой, соответствующий первому вектору.
- Выбирается начальная точка второго вектора, соответствующая конечной точке первого вектора.
- Из второй точки проводится отрезок прямой, соответствующий второму вектору.
- Получившийся отрезок прямой, начинающийся в начальной точке первого вектора и заканчивающийся в конечной точке второго вектора, является результатом сложения этих векторов.
Таким образом, геометрическая интерпретация позволяет наглядно представить процесс сложения неколлинеарных векторов и получить вектор-сумму в виде отрезка прямой линии.
Вопрос-ответ:
Что такое правило сложения неколлинеарных векторов?
Правило сложения неколлинеарных векторов — это метод комбинирования двух или более векторов и получения суммарного вектора. Неколлинеарные векторы — это векторы, которые не лежат на одной прямой.
Как осуществляется сложение неколлинеарных векторов?
Для сложения неколлинеарных векторов, их можно представить в виде направленных отрезков и поместить начало векторов в одну точку. Затем, конец первого вектора становится началом второго вектора, и так далее. Сумма векторов соответствует вектору, который начинается от начала первого вектора и заканчивается в конце последнего вектора.
Зачем нужно правило сложения неколлинеарных векторов?
Правило сложения неколлинеарных векторов является основой для многих физических и математических принципов. Оно позволяет решать задачи, связанные с перемещением, скоростью, силой и другими величинами, представленными векторами. Без этого правила было бы сложно анализировать и моделировать различные физические явления.