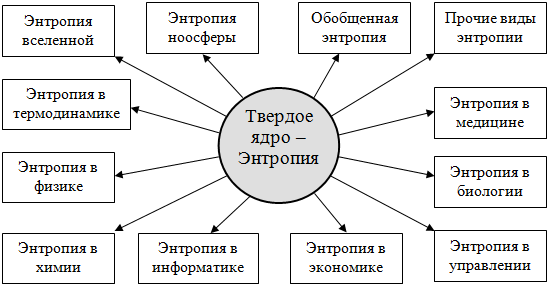
Энтропия – это одна из основных концепций в теории информации и статистической физике. Она является мерой неопределенности или хаоса в системе. Чем выше энтропия, тем больше неупорядоченности или разнородности в системе.
Понятие энтропии было предложено Людвигом Больцманом в конце XIX века и с тех пор оказало огромное влияние на различные области науки.
В статистической физике энтропия определяется как функция состояния, которая характеризует вероятность распределения микросостояний системы. Энтропия позволяет описать неупорядоченность состояний системы и показывает, сколько информации необходимо, чтобы полностью определить ее состояние.
Энтропия является ключевым понятием в теории информации, где она используется для измерения содержания информации в сообщении. Чем более неожиданное сообщение, тем выше энтропия и, соответственно, более информативное оно является.
Что такое функция состояния?
Функция состояния может быть представлена в виде математического выражения или графика, который показывает зависимость между параметрами системы и их вероятностным распределением. Эта функция является ключевым инструментом в физике, теории вероятностей и других науках, где требуется описывать неупорядоченные системы.
Роль функции состояния
Функция состояния играет важную роль в анализе и моделировании различных систем. Она позволяет определить вероятностные характеристики системы, такие как энтропия, энергия и другие статистические величины. Кроме того, функция состояния позволяет предсказывать поведение системы в будущем, основываясь на текущем состоянии и знаниях о вероятностях переходов между состояниями.
Пример
Рассмотрим пример с монеткой. Если бросить монетку, она может упасть либо орлом, либо решкой. Функция состояния для этой системы будет содержать два состояния: «орел» и «решка». При этом вероятность выпадения каждого состояния будет равна 0,5.
Орел: P(орел) = 0,5
Решка: P(решка) = 0,5
Описав функцию состояния для этой системы, можно определить, какая степень неупорядоченности присутствует в броске монетки и сделать прогноз о вероятности выполнения каждого из двух возможных состояний.
Какие параметры характеризуют функцию состояния?

Функция состояния в физике характеризует степень неупорядоченности системы. Она описывает вероятность того, что система пребывает в определенном состоянии. Параметры, которые характеризуют функцию состояния, включают:
1. Энтропия
Энтропия является основным понятием для функции состояния. Она определяет степень неупорядоченности системы и связана с вероятностью возникновения определенного состояния.
2. Вероятности состояний
Функция состояния включает вероятности возникновения каждого состояния системы. Они определяются на основе энергетических уровней системы и статистической механики.
Для удобства представления, параметры функции состояния могут быть организованы в таблицу:
| Параметр | Описание |
|---|---|
| Энтропия | Степень неупорядоченности системы |
| Вероятности состояний | Вероятности возникновения каждого состояния системы |
В совокупности, эти параметры определяют функцию состояния и позволяют описывать поведение физических систем.
Определение функции состояния в терминах неупорядоченности системы.
Функция состояния может быть представлена различными способами, в зависимости от контекста и свойств системы. В физике, для описания хаоса и неупорядоченности, часто используется понятие энтропии — меры неопределенности или неупорядоченности системы. Чем больше энтропия, тем более неупорядоченной или хаотической является система.
Однако, в теории вероятностей функция состояния может быть представлена различными величинами, такими как энтропия Шеннона, энтропия Реньи или энтропия Тsаllis. Каждая из этих функций представляет собой меру сложности или неупорядоченности системы, и используется в различных областях исследований.
Определение функции состояния в терминах неупорядоченности системы позволяет установить связь между степенью хаоса в системе и ее свойствами. Например, она может быть использована для оценки эффективности работы системы, идентификации фазовых переходов или предсказания поведения системы в будущем.
Таким образом, функция состояния является важной концепцией, которая помогает понять и объяснить сложные процессы и системы, связанные с неупорядоченностью и хаосом.
Как определяется степень неупорядоченности системы?
Энтропия
Энтропия — это мера неопределенности или неупорядоченности системы. Чем выше энтропия, тем более неупорядоченная система. Энтропия вычисляется с помощью формулы:
S = — Σ Pi log2 Pi
где Σ обозначает сумму по всем возможным состояниям системы, Pi — вероятность нахождения системы в состоянии i, log2 — логарифм по основанию 2.
Энтропия принимает значения от 0 до бесконечности. Если система находится в состоянии полного порядка, то энтропия равна 0. Если система находится в состоянии полной хаотичности, то энтропия стремится к бесконечности.
Другие функции состояния
Помимо энтропии существуют и другие функции состояния, которые могут использоваться для описания степени неупорядоченности системы. Некоторые из них включают в себя критические показатели, фазовые переходы, показатели Ляпунова и др.
Каждая из этих функций предоставляет свой уникальный подход к определению и измерению степени неупорядоченности системы и может использоваться в различных областях науки и техники.
Роль функции состояния в изучении неупорядоченных систем.
Функция состояния применяется в различных областях науки, таких как физика, химия, биология и информатика. В физике она используется для описания статистических систем, где частицы неупорядочены и взаимодействуют между собой случайным образом.
Одной из основных задач при изучении неупорядоченных систем является определение их энтропии. Энтропия показывает степень неупорядоченности системы и связана с функцией состояния. Чем выше энтропия, тем более неупорядоченной является система.
Функция состояния позволяет оценить вероятность различных состояний системы. Она включает в себя информацию о распределении вероятностей для каждого возможного состояния системы. Таким образом, функция состояния позволяет вычислять различные статистические величины, такие как среднее значение и дисперсия, которые помогают анализировать систему.
Изучение неупорядоченных систем имеет большое практическое значение. Например, понимание степени неупорядоченности может помочь в разработке новых материалов с определенными свойствами или в анализе больших массивов данных. Также функция состояния является основой для создания моделей, которые позволяют прогнозировать поведение системы в будущем.
Как функция состояния помогает в анализе сложных систем?
В анализе сложных систем функция состояния играет важную роль, так как позволяет определить, насколько система находится в стабильном или неустойчивом состоянии. Она позволяет квантифицировать неупорядоченность системы и предоставляет численное значение, отражающее ее порядок или хаос.
Анализ функции состояния позволяет исследователям определить, какие факторы влияют на изменение неупорядоченности системы. Он может помочь предсказать тенденции развития системы и понять, какие изменения могут возникнуть в результате внешнего воздействия.
Функция состояния также может быть использована для сравнения разных систем и выявления общих закономерностей между ними. Она позволяет классифицировать системы по степени неупорядоченности и определить, какие системы более или менее устойчивы или предсказуемы.
Кроме того, функция состояния может быть использована для оценки эффективности управления сложными системами. Она позволяет оценить, насколько система находится в желаемом состоянии и какие меры следует предпринять для достижения оптимального результата.
Таким образом, функция состояния является мощным инструментом в анализе сложных систем. Она позволяет более глубоко понять системные процессы, предсказать их развитие и принять меры для улучшения управления. Использование функции состояния позволяет обнаруживать закономерности и тренды, которые могут быть незаметны при простом визуальном анализе системы.
Примеры функций состояния в разных областях науки и техники.
Физика
В физике функция состояния применяется для описания состояния системы с большим числом взаимодействующих частиц, например, газа или жидкости. Она может характеризовать такие параметры системы, как энтропия, температура, давление и другие физические величины. Функция состояния в физике играет важную роль при решении различных задач, например, при расчете равновесного состояния системы или при изучении термодинамических процессов.
Кибернетика

В кибернетике функция состояния применяется для описания состояния динамической системы, такой как робот, компьютерная программа или сложная система управления. Эта функция может определить, находится ли система в устойчивом состоянии или находится в состоянии неустойчивости. Функция состояния в кибернетике может быть использована для управления системой и предсказания ее поведения.
Экономика
В экономике функция состояния может использоваться для описания состояния рынка, торговли или финансовой системы. Она может характеризовать такие параметры, как уровень инфляции, безработицы, доходы населения и другие экономические показатели. Функция состояния в экономике может помочь анализировать и прогнозировать различные экономические явления и принимать решения на основе полученных данных.
- Функция состояния в физике позволяет оценить степень хаотичности в системе с большим числом взаимодействующих частиц.
- В кибернетике функция состояния используется для описания состояния динамической системы и управления ею.
- В экономике функция состояния помогает анализировать экономические явления и прогнозировать их развитие.
Как функция состояния связана с энтропией системы?
Энтропия системы — это мера неопределенности или неупорядоченности, связанной с ее состоянием. Чем больше энтропия, тем более неупорядоченной является система. Существует математическое определение энтропии, которая связывает ее с функцией состояния:
Математическое определение энтропии системы:
Энтропия системы S, обозначаемая как H(S), может быть вычислена по формуле:
| Термин | Определение |
|---|---|
| Состояние системы | Конкретные значения всех переменных, описывающих систему |
| Вероятность состояния | Вероятность, с которой система находится в данном состоянии |
| Логарифм вероятности | логарифм от обратной вероятности состояния |
Используя эти понятия, мы можем вычислить энтропию системы. Чем равномернее распределены вероятности состояний системы, тем выше ее энтропия. Например, если все состояния системы равновероятны, то энтропия будет максимальной.
Пример:
Рассмотрим систему с 3 состояниями, где каждое состояние имеет вероятность 1/3. Тогда энтропия этой системы будет:
H(S) = — (1/3 * log2(1/3) + 1/3 * log2(1/3) + 1/3 * log2(1/3)) = -3 * (1/3 * log2(1/3)) = log2(3)
Таким образом, энтропия системы равна логарифму от числа возможных состояний системы. Чем больше возможных состояний, тем выше энтропия и тем более неупорядоченной является система.
Функция состояния и энтропия системы взаимосвязаны: энтропия системы является мерой неупорядоченности, связанной с функцией состояния.
Как использование функции состояния может оптимизировать работу системы?
Использование функции состояния может оптимизировать работу системы в нескольких аспектах:
1. Обнаружение проблемных областей
Функция состояния позволяет отслеживать изменения в системе и выявлять области, которые становятся неупорядоченными. Это может помочь идентифицировать проблемы и недостатки, которые могут привести к снижению эффективности работы системы.
2. Принятие решений на основе степени неупорядоченности
Функция состояния может использоваться для определения оптимальных действий в зависимости от текущего состояния системы. Например, если степень неупорядоченности высока, система может автоматически принять решение о перезапуске или улучшении процессов для восстановления порядка.
3. Предупреждение о потенциальных проблемах
На основе функции состояния можно создать систему предупреждений, которая оповещает о возможных проблемах до того, как они повлияют на работу системы. Это позволяет операторам своевременно принимать меры для минимизации негативного влияния на работу системы.
Использование функции состояния позволяет системе быть более гибкой, адаптивной и эффективной. Оно помогает оптимизировать работу системы, улучшать производительность и предотвращать проблемы, что в итоге приводит к повышению качества работы системы в целом.
Вопрос-ответ:
Что такое функция состояния?
Функция состояния — это математическое описание состояния системы, которое позволяет определить ее свойства и характеристики.
Как называется функция, описывающая степень неупорядоченности системы?
Функция, характеризующая степень неупорядоченности системы, называется энтропия.
Зачем нужна функция состояния?
Функция состояния позволяет определить свойства системы, такие как энергия, импульс, температура и др. Она играет важную роль в физике и статистической механике для анализа и изучения поведения системы.
Можно ли с помощью функции состояния определить вероятность нахождения системы в данном состоянии?
Нет, функция состояния сама по себе не определяет вероятность нахождения системы в данном состоянии. Для этого нужна дополнительная информация, например, функция распределения вероятностей.