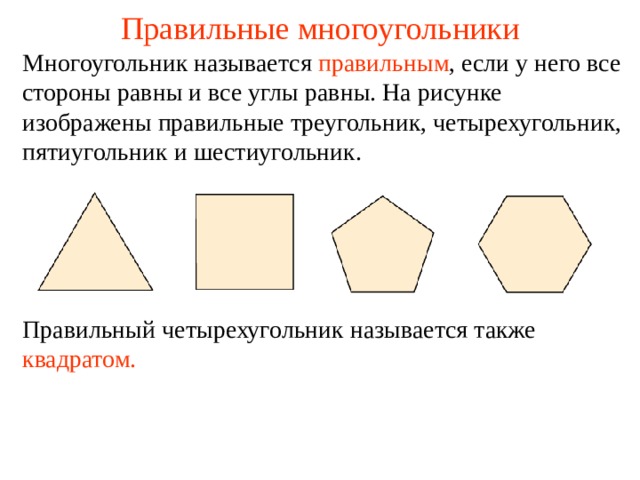
Выпуклым называется многоугольник, у которого все углы внутренние. В отличие от невыпуклых многоугольников, в которых существуют вытянутые углы, выпуклый многоугольник имеет все свои углы меньше 180 градусов. Важно отметить, что выпуклый многоугольник всегда ограниченным.
Выпуклые многоугольники широко применяются в различных областях, таких как геометрия, компьютерная графика, оптимизация и дизайн. Их геометрические свойства очень полезны при решении разнообразных задач. Например, выпуклые многоугольники используются для определения границ объектов в компьютерном зрении, для вычисления видимости в 3D-графике и для создания эффективных алгоритмов рендеринга.
Изучение и понимание выпуклых многоугольников имеет большое значение в математике и других науках. Они являются основным объектом изучения в дискретной геометрии. Более того, основные свойства выпуклых многоугольников могут быть обобщены на размерности выше двух, что позволяет применять их в абстрактных математических моделях и алгоритмах.
Что такое выпуклый многоугольник?
Выпуклым называется многоугольник, у которого все углы меньше 180 градусов и любая прямая, проходящая через две вершины многоугольника, лежит полностью внутри фигуры.
Выпуклый многоугольник является одной из основных геометрических фигур, которая имеет множество свойств и применений.
Существует несколько способов определить, является ли многоугольник выпуклым. Например, можно проверить, что все углы многоугольника не превышают 180 градусов. Также можно проверить, что все диагонали многоугольника лежат внутри фигуры.
Свойства выпуклых многоугольников
- Все внутренние углы выпуклого многоугольника меньше 180 градусов.
- Любая диагональ выпуклого многоугольника лежит внутри фигуры.
- Выпуклый многоугольник всегда можно описать около окружности.
- Площадь выпуклого многоугольника всегда больше нуля.
Применения выпуклых многоугольников
Выпуклые многоугольники широко применяются в геометрии, компьютерной графике и множестве других областей.
Одним из примеров применения выпуклых многоугольников является задача нахождения выпуклой оболочки множества точек. Выпуклая оболочка — это выпуклый многоугольник, который содержит все точки исходного множества.
Выпуклые многоугольники также используются в оптимизации и линейном программировании для нахождения наибольших и наименьших значений функций в ограниченном пространстве.
Кроме того, выпуклые многоугольники играют важную роль в компьютерной графике при отрисовке объектов с помощью полигонов и при вычислении пересечений объектов.
Определение и свойства
Выпуклым называется многоугольник, у которого для любых двух точек A и B, принадлежащих многоугольнику, отрезок AB целиком лежит внутри многоугольника.
У выпуклых многоугольников есть несколько основных свойств:
- Все углы выпуклого многоугольника меньше 180 градусов.
- Любая диагональ выпуклого многоугольника не пересекает его стороны внутри многоугольника.
- Выпуклый многоугольник является ограниченной выпуклой фигурой с конечным числом сторон и углов.
- Сумма внутренних углов выпуклого многоугольника равна (n-2) * 180 градусов, где n — число вершин многоугольника.
Как проверить, что многоугольник выпуклый?
1. Проверка по направлению обхода вершин
Одним из простейших способов проверить, является ли многоугольник выпуклым, является проверка по направлению обхода вершин. Если все вершины многоугольника обходятся по часовой или против часовой стрелки, то многоугольник выпуклый. Для этого можно вычислить векторное произведение каждых двух последовательных ребер и проверить их знаки. Если знаки всех векторных произведений одинаковы, то многоугольник выпуклый. Если знаки разные, то многоугольник невыпуклый.
2. Проверка по внутренним углам
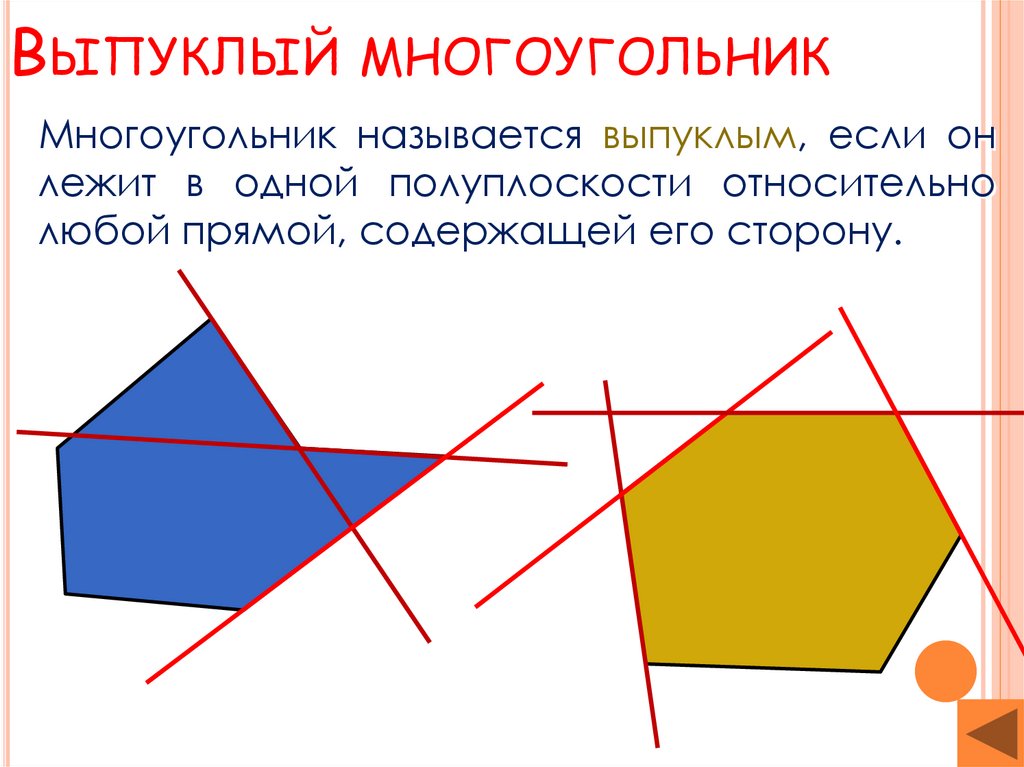
Другим способом проверки выпуклости многоугольника является проверка внутренних углов. Для выпуклого многоугольника все внутренние углы должны быть меньше 180 градусов. Для этого можно вычислить значение каждого внутреннего угла и проверить, что оно меньше 180 градусов. Если хотя бы один угол больше или равен 180 градусов, то многоугольник невыпуклый.
Таким образом, проверка выпуклости многоугольника может быть осуществлена как по направлению обхода вершин, так и по внутренним углам. Каждый из методов имеет свои преимущества и недостатки, и выбор определенного способа зависит от конкретной задачи и доступных вычислительных ресурсов.
Различия между выпуклым и невыпуклым многоугольником
Выпуклым многоугольником называется многоугольник, у которого все внутренние углы меньше 180 градусов. Все его диагонали лежат внутри фигуры. Также выпуклый многоугольник можно определить следующим образом: если взять две точки на его границе, все точки, лежащие на отрезке между этими двумя точками, тоже будут принадлежать многоугольнику.
Невыпуклым многоугольником называется многоугольник, у которого есть хотя бы один внутренний угол больше 180 градусов. В этом случае некоторые диагонали многоугольника будут пересекать его границу и выходить за пределы фигуры. То есть, нарушается условие для выпуклого многоугольника.
Выпуклый и невыпуклый многоугольники имеют существенные отличия, связанные с их формой и свойствами. У выпуклых многоугольников все внутренние углы меньше 180 градусов, что позволяет им быть более упорядоченными и предсказуемыми. Они имеют свойства, которые могут быть использованы в различных теоретических и практических задачах, таких как вычисление площади и периметра, доказательство теорем и т. д.
Невыпуклые многоугольники, в свою очередь, более сложны и неоднозначны с точки зрения своей формы и внутренней структуры. Они могут иметь различные формы в зависимости от положения вершин и внутренних углов. Это делает их более трудными для анализа и использования в математических моделях.
Важно учитывать, что в некоторых случаях может возникнуть необходимость работать как с выпуклыми, так и с невыпуклыми многоугольниками. В зависимости от поставленной задачи, следует выбрать соответствующий подход и использовать соответствующие алгоритмы и методы решения.
Применение выпуклых многоугольников
Выпуклые многоугольники широко применяются в различных областях, где необходимо работать с геометрическими фигурами. Ниже представлены основные сферы применения:
1. Графика и компьютерные игры: выпуклые многоугольники используются для создания разнообразных объектов, таких как фигуры, поверхности и модели. Благодаря своей простоте и эффективности, они позволяют создавать реалистичные и качественные изображения.
2. Компьютерное зрение и обработка изображений: выпуклые многоугольники применяются для анализа и обработки изображений, таких как распознавание объектов, сегментация изображений, а также для выделения контуров и текстур. Их использование позволяет значительно упростить и ускорить алгоритмы обработки изображений.
3. Алгоритмы и оптимизация: нахождение выпуклой оболочки множества точек является одной из основных задач в компьютерной геометрии. Эта задача имеет множество применений, включая решение задач оптимизации, построение выпуклых полиэдральных моделей и аппроксимацию сложных фигур с помощью простых выпуклых многоугольников.
4. Робототехника и автоматизация: выпуклые многоугольники используются для планирования и управления движением роботов. Они позволяют оптимизировать путь робота и избегать препятствий, что особенно важно в промышленных задачах, где требуется точное и безопасное перемещение оборудования.
Применение выпуклых многоугольников способствует упрощению и оптимизации различных задач в геометрии, компьютерных науках и других областях. Их использование позволяет достичь более эффективной и точной обработки данных, создания реалистичных изображений и оптимизации процессов.
Выпуклые многоугольники в программировании и геометрии
В программировании и геометрии выпуклые многоугольники имеют ряд особенностей и применяются для решения различных задач.
1. Площадь и периметр
Вычисление площади и периметра выпуклого многоугольника — одна из основных задач, связанных с ним. Для этого используются различные алгоритмы, такие как алгоритм Грэхема или алгоритм Джарвиса. Они позволяют эффективно вычислять площадь и периметр многоугольника, используя его вершины и стороны.
2. Проверка на выпуклость
Критерий выпуклости многоугольника позволяет определить, является ли многоугольник выпуклым или нет. Существуют различные способы проверки на выпуклость, например, по последовательности углов или по угловым коэффициентам сторон. Это позволяет программистам и математикам быстро и точно определить, имеет ли многоугольник выпуклую форму или нет.
Выпуклые многоугольники являются важными объектами в программировании и геометрии, и они находят широкое применение в различных областях, таких как компьютерная графика, алгоритмы оптимизации, географические информационные системы и другие. Преимущество выпуклых многоугольников заключается в их простоте и понятности, что делает их инструментом выбора при решении геометрических задач.
Использование выпуклых многоугольников в программировании и геометрии требует глубокого понимания и знания соответствующих алгоритмов и методов обработки данных.
Примеры выпуклых многоугольников
Прямоугольник
Прямоугольник — это четырехугольник с противоположными сторонами, равными и параллельными. Все его углы прямые. Прямоугольник является выпуклым многоугольником, так как все его углы равны 90 градусам.
Пятиугольник
Пятиугольник — это многоугольник с пятью сторонами и пятью углами. Если внутри пятиугольника провести любые две диагонали, то они не пересекутся внутри фигуры. Пятиугольник также является выпуклым многоугольником.
Шестиугольник
Шестиугольник — это многоугольник с шестью сторонами и шестью углами. Если внутри шестиугольника провести любые две диагонали, то они также не пересекутся внутри фигуры. Шестиугольник является примером выпуклого многоугольника.
- Прямоугольник
- Пятиугольник
- Шестиугольник
Выпуклые многоугольники имеют множество применений, включая геометрические моделирование, компьютерную графику, оптимизацию и другие области. Определение и свойства выпуклых многоугольников играют ключевую роль в решении многих задач и проблем.
Связанные термины и понятия
Рассмотрим некоторые термины и понятия, связанные с многоугольниками:
Ребро
Ребро многоугольника — это отрезок, соединяющий две вершины.
Вершина
Вершина многоугольника — это точка пересечения двух или более ребер.
Угол
Угол многоугольника — это область пространства между двумя смежными ребрами, ограниченная вершиной.
Диагональ
Диагональ многоугольника — это отрезок, соединяющий две несмежные вершины.
- Диагонали выпуклого многоугольника — это отрезки, соединяющие любые две несмежные вершины многоугольника и не пересекающиеся внутри многоугольника.
Выпуклый угол
Выпуклый угол — это угол, все точки которого лежат внутри или на границе многоугольника.
Выпуклая оболочка
Выпуклая оболочка — это наименьший выпуклый многоугольник, содержащий все точки данного множества.
- Выпуклая оболочка может быть представлена в виде множества вершин или в виде последовательности вершинных ребер.
Вопрос-ответ:
Что такое выпуклый многоугольник?
Выпуклым называется многоугольник, все внутренние углы которого не превышают 180 градусов.
Как определить, является ли многоугольник выпуклым?
Чтобы убедиться, что многоугольник выпуклый, необходимо проверить, что все внутренние углы многоугольника не превышают 180 градусов.
Чем отличается выпуклый многоугольник от невыпуклого?
Выпуклый многоугольник имеет все внутренние углы, не превышающие 180 градусов. В то же время, невыпуклый многоугольник содержит хотя бы один внутренний угол, превышающий 180 градусов.
Какие свойства имеют выпуклые многоугольники?
Выпуклые многоугольники имеют несколько основных свойств: все углы многоугольника не превышают 180 градусов, любой отрезок, соединяющий две точки на границе выпуклого многоугольника, лежит внутри него, и выпуклый многоугольник не имеет самопересечений.
Каково применение выпуклых многоугольников?
Выпуклые многоугольники широко применяются в геометрии и компьютерной графике. Они используются для моделирования и отображения различных объектов, таких как полигоны, зоны видимости, оболочки объектов и многие другие.