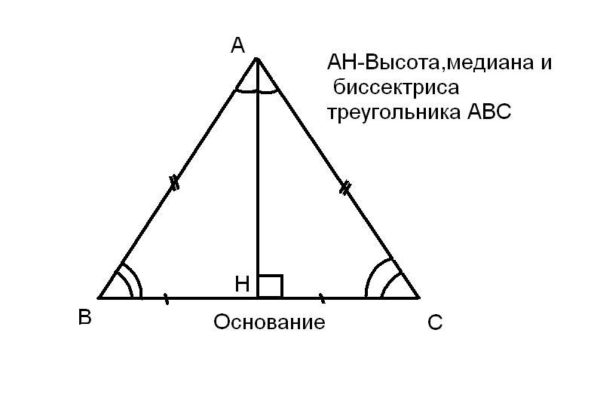
Равнобедренные треугольники – это фигуры, у которых две из трех сторон равны между собой. В геометрии каждая сторона треугольника имеет свое название, которое помогает нам лучше понять его свойства и особенности.
В равнобедренном треугольнике есть несколько основных сторон, некоторые из которых имеют свои специфические названия. Самые главные стороны треугольника — это его основания и боковые стороны. Основания – это две равные стороны, он-лайн относящиеся к одному углу вершины треугольника. Боковые стороны – это третья сторона треугольника, она соединяет вершину соседнего угла со стороной противоположного основания.
Стоит отметить, что равнобедренный треугольник обладает несколькими интересными свойствами. Например, у него также равны два угла при основании и высота, опущенная из вершины равна середине основания. Эти свойства делают равнобедренный треугольник особенным и легко определяемым. Знание названия всех его сторон помогает более глубоко исследовать его свойства и использовать эти знания в решении различных задач и проблем.
Определение равнобедренного треугольника
В равнобедренном треугольнике противоположные стороны, не равные базе, называются боковыми сторонами. База равнобедренного треугольника — это сторона, которая отличается от боковых сторон.
Также равнобедренный треугольник имеет два равных угла, расположенных напротив равных сторон. Эти углы называются углами при основании, а третий угол называется вершинным углом. Вершинный угол равнобедренного треугольника всегда меньше углов при основании.
Соотношение сторон
В равнобедренном треугольнике две стороны имеют одинаковую длину, а третья сторона называется основанием. Соотношение сторон в таком треугольнике можно выразить следующим образом:
- Основание и равные стороны образуют изоскелес треугольник.
- Основание образует параллельные стороны, а третья сторона называется боковой стороной.
Соотношение сторон в равнобедренном треугольнике позволяет нам рассчитать различные параметры этой фигуры, такие как площадь и периметр. Зная длину одной из равных сторон и длину основания, мы можем применить формулы и получить нужные значения.
Важно отметить, что в равнобедренном треугольнике все углы при основании равны, а противолежащие им углы при равных сторонах равны между собой.
Соотношение сторон в равнобедренном треугольнике является фундаментальным свойством этой геометрической фигуры и позволяет нам лучше понять форму и особенности треугольника.
Свойства равнобедренного треугольника
В равнобедренном треугольнике:
- два угла при основании равны;
- два основания равны;
- определенная точка пересечения медиан называется вершиной треугольника;
- высота, опущенная из вершины треугольника, является биссектрисой;
- площадь треугольника можно найти по формуле: S = (b * h) / 2, где b — длина основания, h — длина высоты.
Свойства равнобедренного треугольника позволяют упростить решение задач и находить дополнительные значения его сторон и углов.
Названия сторон равнобедренного треугольника
При обозначении сторон равнобедренного треугольника обычно используют следующие буквы:
| Буква | Сторона |
|---|---|
| a | Боковая сторона треугольника |
| b | Боковая сторона треугольника |
| c | Основание треугольника |
Таким образом, боковые стороны равнобедренного треугольника обозначаются буквами a и b, а основание треугольника – буквой c.
С помощью этих обозначений можно записать и решать различные геометрические задачи, касающиеся равнобедренных треугольников.
База
Основание равнобедренного треугольника играет важную роль в его конструкции и свойствах. Оно является отрезком, соединяющим вершины треугольника и образует с ними углы. Также основание определяет длину и ширину треугольника, а также его площадь и периметр.
В геометрии равнобедренных треугольников основание является одной из ключевых характеристик, которая помогает определить его свойства и решить различные задачи. Знание основания треугольника позволяет установить соотношения между его сторонами и углами, а также применить соответствующие формулы и теоремы для решения задачи.
Равнобедренные стороны
В равнобедренном треугольнике две стороны имеют одинаковую длину. Эти стороны называются равнобедренными сторонами. Они всегда противоположны углу, образующему основание треугольника.
Равнобедренные стороны обозначаются обычно буквой ‘a’. В формуле для расчета площади равнобедренного треугольника, равнобедренные стороны считаются равными и обозначаются как ‘a’ и ‘b’, а основание обозначается буквой ‘c’.
Для упрощения обозначений, в работе с равнобедренными треугольниками можно использовать другие обозначения сторон, например, ‘AB’ и ‘AC’ или ‘BC’ и ‘AC’.
Знание равнобедренных сторон треугольника помогает в решении различных геометрических задач, таких как нахождение площади, периметра, высоты или углов треугольника.
Вопрос-ответ:
Что такое равнобедренный треугольник?
Равнобедренный треугольник — это треугольник, у которого две стороны равны друг другу. В равнобедренном треугольнике углы при основании равны.
Если в треугольнике две равные стороны, то какие это стороны?
Если в треугольнике две равные стороны, то это стороны, которые величиной равны одинаковым отрезкам между вершиной и основанием.
Как называются равные стороны равнобедренного треугольника?
Равные стороны равнобедренного треугольника называются бедрами, а третья сторона, неравная бедрам, называется основанием равнобедренного треугольника.
Что можно сказать про углы равнобедренного треугольника?
В равнобедренном треугольнике углы при основании равны, а угол напротив основания называется вершинным углом. Вершинный угол равнобедренного треугольника может быть как острый, так и тупой.
Можно ли назвать основание и боковые стороны по-другому в равнобедренном треугольнике?
Да, основание и боковые стороны равнобедренного треугольника могут иметь разные названия. Основание треугольника можно называть основанием, а боковые стороны — бедрами. Однако, в разных источниках и литературе названия могут варьироваться, но суть остается неизменной.