Какая трапеция называется равнобедренной прямоугольной

Трапецией называется четырехугольник, у которого одна пара сторон параллельна, но не равна другой паре сторон.

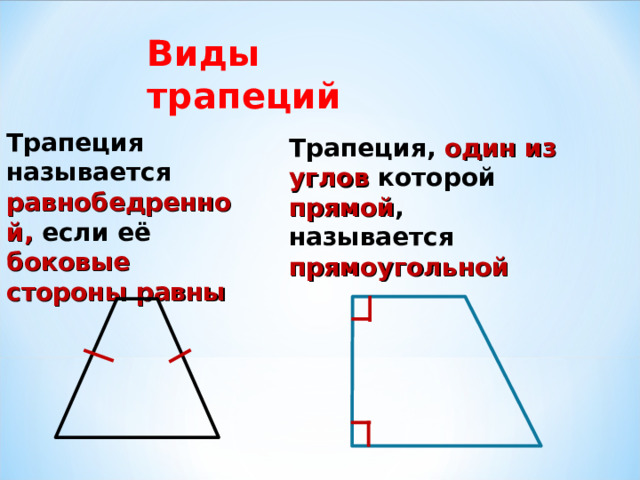
Равнобедренной трапецией называется трапеция, у которой длины двух противоположных сторон равны. Это означает, что два угла трапеции между боковыми сторонами также равны.

Прямоугольной трапецией называется трапеция, у которой один из углов является прямым углом, то есть равен 90 градусам.

Соединив эти два определения, мы получаем трапецию, которая имеет две равные стороны и прямой угол. Такую трапецию называют равнобедренной прямоугольной.

Содержание

Что такое равнобедренная прямоугольная трапеция?

Угол между основаниями называется вершиной трапеции. В случае равнобедренной прямоугольной трапеции, это угол всегда прямой (равный 90 градусам).

Как и в случае с обычной трапецией, равнобедренная прямоугольная трапеция имеет два непараллельных основания и две параллельные боковые стороны.

Характеристики равнобедренной прямоугольной трапеции:

1. Две пары равных сторон;

2. Один прямой угол (равный 90 градусам);

3. Два непараллельных основания;

4. Две параллельные боковые стороны.

Свойства равнобедренной прямоугольной трапеции:

1. Сумма углов при основании трапеции равна 180 градусам;

2. Угол между диагоналями трапеции равен 90 градусам;

3. Равнобедренные треугольники, образованные диагональю и боковой стороной трапеции, равны по гипотенузе и одному из острых углов.

Равнобедренная прямоугольная трапеция является основой для ряда геометрических конструкций и задач. Она имеет ряд характерных свойств, которые используются при решении различных математических задач.

Пример равнобедренной прямоугольной трапеции:
	_____ \ /\ \ / \ \/____\

Определение равнобедренной прямоугольной трапеции

Эта геометрическая фигура имеет следующие характеристики:

1. Равные стороны

В равнобедренной прямоугольной трапеции две противоположные стороны равны друг другу. Это значит, что боковые стороны параллельны и имеют одинаковую длину, а основания могут быть разной длины.

2. Прямые углы

В равнобедренной прямоугольной трапеции два противоположных угла являются прямыми углами, то есть равны 90 градусам. Остальные два угла могут быть различными и в сумме составляют 180 градусов.

Эти характеристики делают равнобедренную прямоугольную трапецию особой и заслуживающей отдельного определения.

Основные свойства равнобедренной прямоугольной трапеции

Основные свойства равнобедренной прямоугольной трапеции:

У равнобедренной прямоугольной трапеции основания параллельны.
Боковые стороны равны по длине.
Углы при основаниях равны и являются прямыми углами.
Диагонали перпендикулярны между собой и равны.
Высота, опущенная из вершины равнобедренной прямоугольной трапеции на основание, является медианой.
Площадь равнобедренной прямоугольной трапеции можно найти, используя формулу S = ((a + b) * h) / 2, где a и b — длины оснований, h — высота треугольника, образованного медианой и одной из боковых сторон.
Периметр равнобедренной прямоугольной трапеции можно найти, используя формулу P = a + b + 2c, где a и b — длины оснований, c — длина боковой стороны.

Зная основные свойства равнобедренной прямоугольной трапеции, мы можем использовать их для решения геометрических задач и вычислений.

Как образуется равнобедренная прямоугольная трапеция

Свойства равнобедренной прямоугольной трапеции:

Две противоположные стороны равны (a = c).
Один из углов прямой (90 градусов).
Основания трапеции (a и c) перпендикулярны друг другу.
Боковые стороны трапеции (b и d) параллельны и равны.

Равнобедренную прямоугольную трапецию можно сконструировать следующим образом:

Нарисуйте прямоугольник ABCD, в котором противоположные стороны AB и CD равны.
Проведите диагонали AC и BD внутри прямоугольника.
Точка пересечения диагоналей (точка O) будет центром симметрии прямоугольника и задаст прямую угловую точку (угол AOD).
От точки O отложите равные отрезки OA и OC, и проведите прямые, параллельные диагоналям AC и BD, соединив точки A и C с соответствующими точками на противоположных сторонах прямоугольника.
Трапеция ABCD с боковыми сторонами AD и BC будет равнобедренной прямоугольной трапецией.

Таким образом, равнобедренная прямоугольная трапеция образуется путем построения диагоналей в прямоугольнике и проведения параллельных линий через точку пересечения диагоналей.

Формула площади равнобедренной прямоугольной трапеции

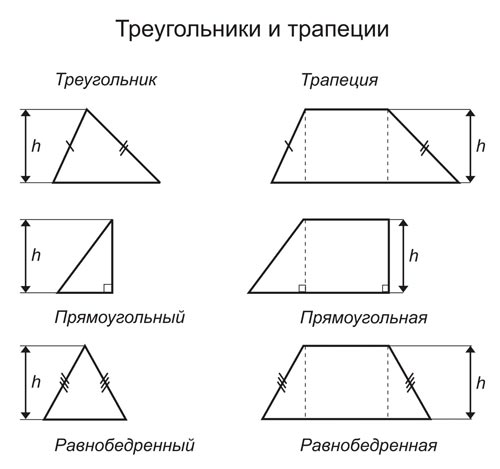
Измеряем стороны трапеции и обозначаем их:

Основания трапеции: a и b

Высота трапеции: h

Формула для расчета площади равнобедренной прямоугольной трапеции:

S = (a + b) * h / 2

Выразим площадь через основания и высоту:

S = (a + b) / 2 * h

Таким образом, площадь равнобедренной прямоугольной трапеции равна половине суммы длин оснований, умноженной на высоту.

Пример:

Для равнобедренной прямоугольной трапеции с длиной основания a = 5, длиной основания b = 8 и высотой h = 6:

S = (5 + * 6 / 2 = 13 * 6 / 2 = 39

Площадь равнобедренной прямоугольной трапеции равна 39 квадратных единиц.

Формула периметра равнобедренной прямоугольной трапеции

Периметр равнобедренной прямоугольной трапеции можно рассчитать с помощью следующей формулы:

P = a + b + c + d

где:

a и b — это основания трапеции,

c и d — это боковые стороны трапеции.

Таким образом, чтобы найти периметр равнобедренной прямоугольной трапеции, необходимо сложить длины всех ее сторон.

Например, если основания равны 5 см, а боковые стороны равны 3 см, то периметр можно найти по формуле:

P = 5 + 5 + 3 + 3 = 16 см

Таким образом, периметр равнобедренной прямоугольной трапеции с указанными размерами будет равен 16 см.

Примеры использования равнобедренной прямоугольной трапеции

Архитектура: Равнобедренные прямоугольные трапеции часто используются в архитектуре при проектировании зданий. Они могут быть использованы в каркасной конструкции крыши, а также в дизайне окон и дверей. Например, крыши некоторых домов имеют форму равнобедренной прямоугольной трапеции.
Инженерия: Равнобедренные прямоугольные трапеции находят применение в различных отраслях инженерии. Они могут использоваться в конструкции мостов и наклонных плоскостей. Также, они могут быть использованы для создания устойчивых и прочных фундаментов.
Дизайн: Равнобедренные прямоугольные трапеции также могут быть использованы в дизайне и художественных проектах. Они могут быть использованы в создании уникальных геометрических узоров, а также служить основой для создания интересных композиций.
Математика: Равнобедренные прямоугольные трапеции используются в математике для решения различных задач и вычислений. Они могут быть использованы для расчета площади фигуры, определения длин сторон и углов, а также для изучения свойств и особенностей трапеций в общем.

Это только некоторые примеры использования равнобедренной прямоугольной трапеции. Благодаря своим особенностям и уникальным свойствам, эта фигура находит применение в различных областях и предоставляет широкие возможности для творчества и практического использования.

Отличия равнобедренной прямоугольной трапеции от других фигур

Во-первых, у равнобедренной прямоугольной трапеции две равные наклонные стороны. Это значит, что углы при основаниях равны между собой. Такие трапеции имеют особую геометрическую симметрию, что делает их узнаваемыми и интересными.

Во-вторых, она имеет два прямых угла. Это значит, что прилегающие к основаниям стороны образуют прямые углы с основаниями. Такая особенность прямоугольной трапеции делает ее похожей на прямоугольник, но с одним параллельным основанием.

В-третьих, равнобедренная прямоугольная трапеция имеет свойство симметрии относительно оси симметрии, проходящей через середину наклонной стороны. Такая симметрия делает эту трапецию интересной и эстетически привлекательной.

В-четвертых, такая трапеция имеет связь с прямоугольным треугольником, так как углы при основаниях равны между собой и сумма этих углов равна 90 градусам.

Наконец, равнобедренная прямоугольная трапеция удобна в использовании при решении геометрических задач, а также в строительстве и архитектуре, благодаря своим особым свойствам и геометрическим характеристикам.