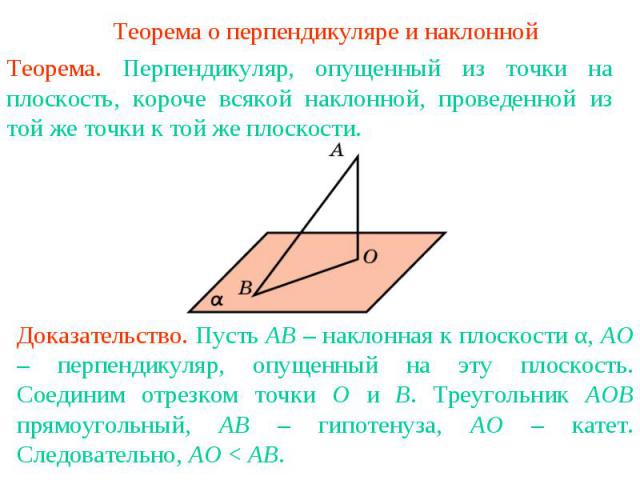
В геометрии существует несколько типов прямых, которые могут быть проведены из точки: наклонные, перпендикулярные, параллельные и многие другие. Однако есть особый тип отрезка, который является наиболее важным и широко используется в различных математических проблемах. Этот отрезок называется главной.
Главная – это отрезок, который проведен из некоторой точки и перпендикулярен прямой. Он имеет свойства, позволяющие решать различные задачи на плоскости. Главная является кратчайшим из всех возможных отрезков, проведенных из точки к прямой, и она всегда пересекает ее под прямым углом.
Главная имеет ряд применений в различных областях математики и физики. Например, в геометрии она используется для построения перпендикуляров и определения взаимного расположения прямых. В физике главная используется, например, при изучении световых лучей и распространении звука.
Определение отрезка, проведенного из точки к прямой, меньшего всех наклонных
Для проведения перпендикулярной из точки к прямой, нужно провести линию, которая будет пересекать данную прямую и образовывать прямой угол с ней. Это позволит получить отрезок, являющийся перпендикулярной.
Перпендикулярная является важным понятием в геометрии и находит применение в различных областях, таких как строительство, картография и физика. Она служит для определения прямых, углов и расстояний, а также для построения перпендикулярной линии, которая может быть использована в различных задачах и вычислениях.
Геометрическое определение перпендикулярной
Перпендикулярная линия проходит через данную точку и образует прямой угол с данной прямой. Другими словами, угол между перпендикулярной и данной прямой равен 90 градусам, или π/2 радиан.
Математическое определение перпендикулярной
Если прямая AB перпендикулярна прямой CD, то можно записать следующее математическое уравнение: AB ⊥ CD. Для перпендикулярной линии выполняются следующие эффективные условия:
- Произведение их коэффициентов наклона равно -1:
- Угол между перпендикулярной линией и данной прямой равен 90 градусам:
mAB * mCD = -1
∠ABD = 90°
Перпендикулярная является важным инструментом в геометрии и обладает своими уникальными свойствами. Знание определения перпендикулярной позволяет решать сложные задачи, связанные с построением и вычислениями в различных дисциплинах.
Отрезок в геометрии
Отрезки могут быть различной длины и направленности. Если отрезок соединяет две разные точки, он называется нераспространяющимся отрезком. Если отрезок распространяется бесконечно в одном направлении, он называется полуотрезком. Если отрезок распространяется бесконечно в обе стороны, он называется прямой.
Отрезки могут иметь разные свойства и геометрические характеристики, такие как длина, положение на плоскости, параллельность или пересечение с другими отрезками и прямыми. Они играют важную роль в конструктивной геометрии, теории вероятности и других областях науки и математики.
Один из интересных вопросов, связанных с отрезками, это названия для различных отрезков, которые можно провести из точки к прямой. Один из таких отрезков — высота треугольника — является отрезком, проведенным из вершины перпендикулярно основанию треугольника. Другой отрезок — биссектриса треугольника — является отрезком, делящим угол треугольника на две равные части. Эти отрезки имеют свои названия и свойства, которые широко используются в геометрии и связанных областях математики.
Точка и прямая в геометрии
Прямая — это геометрическая фигура, которая имеет бесконечную длину, но нулевую ширину. Она также определяется своим положением в пространстве с помощью уравнения прямой или нескольких точек, через которые она проходит.
Один из основных элементов, связывающих точку с прямой, — это отрезок, проведенный из точки к прямой. Отрезок — это участок прямой, ограниченный двумя точками. В случае проведения отрезка из точки к прямой, конечная точка отрезка на прямой является проекцией данной точки на эту прямую.
Особенность отрезка, проведенного из точки к прямой, заключается в том, что он является самым коротким отрезком, который соединяет данную точку с прямой. Это означает, что любой другой отрезок, проведенный из данной точки и наклонный к прямой, будет иметь большую длину в сравнении с первым отрезком.
| Тип отрезка | Длина отрезка |
|---|---|
| Отрезок, проведенный из точки к прямой | Минимальная длина |
| Наклонный отрезок, проведенный из точки к прямой | Большая длина |
Таким образом, отрезок, проведенный из точки к прямой, является самым коротким из всех возможных отрезков, соединяющих данную точку с этой прямой.
Наклонные в геометрии
В геометрии наклонной называют отрезок, проведенный из точки к прямой таким образом, что его длина меньше любой другой наклонной, проведенной из данной точки.
Наклонные имеют важное значение в геометрии и используются при решении различных задач. Они помогают определить расстояние от точки до прямой, а также угол между прямой и отрезком.
Для построения наклонных можно использовать различные инструменты и методы. Например, можно воспользоваться угловым инструментом, треугольником или компасом. Важно точно измерять и строить отрезки, чтобы получить правильный результат.
Применение наклонных в геометрии позволяет решать разнообразные задачи, связанные с построением и измерением отрезков, а также определением углов и расстояний. Они являются одним из основных элементов работы с геометрическими фигурами и фигурами на плоскости.
Использование наклонных полезно как в школьной программе по геометрии, так и в повседневной жизни. Например, для построения зданий, мостов или дорог часто требуется вычислить угол наклона, чтобы обеспечить безопасность и надежность конструкции.
Примеры задач, связанных с наклонными:
- Построение прямоугольника, зная одну из его диагоналей и угол наклона
- Определение длины отрезка, проведенного из точки к прямой, используя наклонные
- Решение задач на построение треугольников с заданными углами и длинами сторон
Отрезок проведенный из точки к прямой

Перпендикуляр может быть проведен из точки к прямой, если он пересекает прямую под прямым углом. То есть, линия, проходящая через эту точку и перпендикулярно прямой, будет образовывать прямой угол с прямой.
Отрезок, являющийся перпендикуляром, всегда короче любой наклонной, проведенной из этой точки к прямой. Это свойство обусловлено геометрической природой перпендикуляра и его определением.
Построение перпендикуляра из точки к прямой может быть осуществлено различными методами, такими, как использование углов, конструкции вспомогательной прямой, использование прямой и компаса и другие.
Поиск отрезка, меньшего всех наклонных
Для нахождения отрезка, который меньше всех наклонных, необходимо провести отрезок из точки к прямой и сравнить его длину с длинами всех наклонных, проведенных из этой точки. Отрезок, который окажется меньше всех остальных, будет искомым отрезком.
Шаги поиска отрезка:
- Выберите точку, из которой будет проводиться отрезок к прямой.
- Проведите отрезок из выбранной точки к прямой.
- Измерьте длину проведенного отрезка.
- Проведите все возможные наклонные из выбранной точки.
- Измерьте длины каждой наклонной.
- Сравните длину проведенного отрезка с длинами всех наклонных.
- Выберите отрезок, длина которого меньше всех остальных.
Таким образом, выполнение описанных шагов поможет найти отрезок, который меньше всех наклонных, проведенных из заданной точки к прямой.
Алгоритм нахождения отрезка
Для нахождения отрезка, проведенного из точки к прямой и являющегося самым коротким отрезком, можно использовать следующий алгоритм:
- Выбрать произвольную точку на прямой и обозначить ее координаты (x1, y1).
- Вычислить уравнение прямой вида y = kx + b, где k — это угловой коэффициент прямой, а b — свободный член.
- Найти перпендикулярную прямую, проходящую через данную точку и обозначить ее уравнение вида y = -1/kx + c, где c — свободный член для перпендикулярной прямой.
- Найти точку пересечения перпендикулярной прямой и исходной прямой. Обозначить ее координаты (x2, y2).
- Найти длину отрезка, используя формулу для расстояния между двумя точками: d = sqrt((x2 — x1)^2 + (y2 — y1)^2).
Таким образом, найденный отрезок будет являться самым коротким отрезком, проведенным из данной точки к исходной прямой.
| Шаг | Выполняемые действия |
|---|---|
| 1 | Выбираем точку на прямой |
| 2 | Вычисляем уравнение прямой |
| 3 | Находим перпендикулярную прямую |
| 4 | Находим точку пересечения прямых |
| 5 | Вычисляем длину отрезка |
Используя данный алгоритм, мы можем определить самый короткий отрезок, проведенный из точки к прямой. Это может быть полезно, например, при поиске кратчайшего пути или оптимального расположения объектов относительно прямых.
Применение отрезка в геометрии
1. Измерение расстояний
Отрезок представляет собой участок прямой между двумя конечными точками. Полученные измерения могут быть использованы для определения расстояния между объектами в пространстве. Например, можно измерить расстояние между двумя городами или длину стороны объекта.
2. Построение графиков
Отрезок может быть использован для построения графиков различных функций. Например, на координатной плоскости можно построить отрезок от точки (0, 0) до точки с заданными координатами (x, y), что позволяет визуализировать значение функции на заданных участках.
Кроме того, отрезок может быть использован для построения линейной регрессии и аппроксимации данных.
3. Решение задач
Отрезок может быть использован для решения различных геометрических задач. Например, с помощью отрезка можно найти кратчайший путь между двумя точками на плоскости, а также определить положение точки относительно прямой или других геометрических фигур.
В конечном счете, отрезок является важным инструментом в геометрии и находит широкое применение в решении различных задач из этой области знаний.
Вопрос-ответ:
Как называется отрезок проведенный из точки к прямой который меньше любой наклонной проведенной из другой точки?
Такой отрезок называется высотой треугольника.
Что такое высота треугольника?
Высота треугольника — это отрезок, проведенный из вершины треугольника к прямой, содержащей противоположную сторону и перпендикулярной к ней.
Как определить высоту треугольника?
Для определения высоты треугольника нужно провести перпендикуляр из вершины треугольника к прямой, содержащей противоположную сторону, и найти точку пересечения.
Чем высота треугольника отличается от наклонной?
Высота треугольника отличается от наклонной тем, что она проведена из вершины треугольника к прямой, содержащей противоположную сторону, перпендикулярно к ней, в то время как наклонная проведена из какой-либо другой точки к прямой.
Зачем нужна высота треугольника?
Высота треугольника помогает нам находить площадь треугольника, определять его свойства и решать различные задачи, связанные с треугольниками.