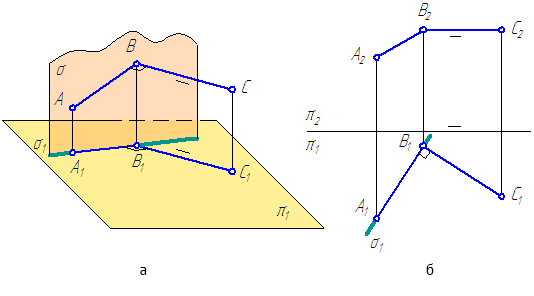
Параллельность проекций прямой относительно оси z является одним из основных принципов в трехмерной графике и компьютерной графике. Этот принцип позволяет нам работать с объектами, проектируемыми на плоскость, с учетом их позиции в пространстве.
Когда мы проецируем точки прямой на плоскость, мы получаем две проекции: проекцию на плоскость XY (план проекции) и проекцию на плоскость XZ (фронтальная проекция). Если параллельные прямые в трехмерном пространстве имеют одни и те же фронтальные проекции, то их проекции на плоскость XY также будут параллельными. Таким образом, параллельность проекций прямой относительно оси z сохраняется в трехмерном пространстве и на плоскости проекций.
Данное свойство имеет важное значение при создании трехмерных моделей и отображении их на двумерном экране. Оно позволяет реалистично отобразить графические объекты и сохранить их иерархические и пространственные отношения.
Раздел 1: Изучение основных понятий
Перед началом изучения параллельности проекций прямой относительно оси z, необходимо понять некоторые важные понятия, связанные с этой темой.
1. Прямая. Прямая — это бесконечно длинная и прямая линия, которая не имеет концов. В геометрии прямую можно определить как кратчайшее расстояние между двумя точками.
2. Ось z. Ось z — это одна из трех осей трехмерной системы координат. Она перпендикулярна плоскостям xOy и простирается вверх и вниз. Ось z используется для определения третьей координаты точки в пространстве.
3. Проекция. Проекция — это изображение объекта на проекционную плоскость. В контексте параллельности проекций прямой относительно оси z, рассматриваются две проекции — проекция на плоскость xOy и проекция на плоскость yOz.
4. Параллельность. Параллельность — это свойство объектов, которые движутся или находятся на постоянном расстоянии друг от друга. В анализе параллельности проекций прямой относительно оси z, рассматриваются две проекции — проекция на плоскость xOy и проекция на плоскость yOz — и исследуется их взаимное расположение и связь.
| Термин | Определение |
|---|---|
| Прямая | Бесконечно длинная и прямая линия без концов |
| Ось z | Одна из трех осей трехмерной системы координат, перпендикулярная плоскостям xOy |
| Проекция | Изображение объекта на проекционную плоскость |
| Параллельность | Свойство объектов, которые движутся или находятся на постоянном расстоянии друг от друга |
Прямая и ее проекции
Прямая имеет различные свойства и характеристики, одной из которых является ее проекция. Проекция прямой — это изображение прямой на плоскость. Она может быть получена путем опускания перпендикуляров от точек прямой на плоскость.
Проекции прямой могут быть параллельными или пересекающимися. В случае параллельных проекций, все перпендикуляры опускаются с прямой на одной и той же плоскости. В случае пересекающихся проекций, перпендикуляры опускаются с прямой на две разные плоскости.
Параллельные проекции прямой имеют следующие особенности:
| Название | Описание |
|---|---|
| Горизонтальная проекция | Проекция прямой на горизонтальную плоскость. |
| Вертикальная проекция | Проекция прямой на вертикальную плоскость. |
| Фронтальная проекция | Проекция прямой на плоскость, перпендикулярную горизонтальной и вертикальной плоскостям. |
Параллельные проекции прямой часто используются при построении различных графических изображений и конструкций в инженерии и архитектуре. Знание особенностей и свойств этих проекций позволяет упростить решение различных геометрических задач и создание точных и качественных конструкций.
Параллельность проекций
Для понимания этого свойства необходимо представить себе трехмерное пространство, где оси x и y лежат в одной плоскости, а ось z перпендикулярна этой плоскости. Проекция прямой на плоскость xy получается путем отбрасывания координаты z.
Если две прямые параллельны в трехмерном пространстве, то их наклоны по осям x, y и z будут одинаковыми. При отбрасывании координаты z и проецировании прямых на плоскость xy, их наклоны также останутся одинаковыми. Это означает, что проекции параллельных прямых также будут параллельными на плоскости xy.
Параллельность проекций имеет множество практических применений, особенно в области компьютерной графики и инженерного моделирования. Зная, что проекции параллельных прямых остаются параллельными, можно легко представлять и визуализировать объекты и их движение на плоскости xy.
Ось z
Ось z проходит через центр координат и перпендикулярна плоскости, образуемой осями x и y. Она направлена вверх из плоскости, обозначая глубину или высоту объекта в трехмерном пространстве.
Ось z играет важную роль в компьютерной графике и трехмерном моделировании. Она позволяет реализовать эффекты глубины и объемности в визуальных приложениях, таких как компьютерные игры и симуляции.
Параллельность проекций прямой относительно оси z означает, что если две или больше прямых параллельны оси z, их проекции на плоскость x-y также будут параллельны. Это свойство играет важную роль в анализе и визуализации трехмерных объектов.
Раздел 2: Связь между проекциями прямой и осью z
Проекция прямой на плоскость xy и ось z в параллельных проекциях имеет связь, которая определяет положение и форму прямой в трехмерном пространстве. Эта связь позволяет нам понять, как две параллельные проекции прямой влияют на ее общую форму и рельеф.
Проекция прямой на плоскость xy может быть представлена как линия, которая лежит на этой плоскости и пересекает ее точкой пересечения с осью z. Если прямая параллельна оси z, то ее проекция на плоскость xy будет прямой линией, а точка пересечения с осью z будет находиться на бесконечности.
Ось z играет важную роль в определении формы и положения прямой в трехмерном пространстве. Она указывает направление и глубину прямой относительно наблюдателя. Если прямая лежит на оси z, то ее проекция на плоскость xy будет вертикальной линией, а форма прямой будет плоской и одномерной. Если прямая параллельна плоскости xy, то ее проекция на эту плоскость будет горизонтальной линией, а форма прямой будет плоской и одномерной.
В общем случае, проекция прямой на плоскость xy и ось z определяют ее трехмерное положение и форму. Это позволяет нам анализировать пространственные отношения между прямыми и понимать их взаимное расположение.
Векторные координаты прямой
Векторные координаты прямой позволяют нам описать ее положение в трехмерном пространстве. Для этого нам понадобятся две точки на прямой, которые мы будем обозначать A и B. Вектор, проведенный из точки A в точку B, называется направляющим вектором прямой.
Если A(x₁, y₁, z₁) и B(x₂, y₂, z₂) — координаты точек A и B соответственно, то вектор AB имеет следующие компоненты:
- Компонента x: ABx = x₂ — x₁
- Компонента y: ABy = y₂ — y₁
- Компонента z: ABz = z₂ — z₁
Таким образом, векторные координаты прямой можно записать в виде AB = (ABx, ABy, ABz).
Эти векторные координаты позволяют нам определить различные свойства и характеристики прямой, такие как ее направление, углы между прямой и осями координат, расстояние между двумя параллельными прямыми и т.д.
Проекции прямой относительно оси z
При рассмотрении трехмерных объектов в пространстве, часто возникает необходимость работать с их проекциями на плоскости. Проекциями называются изображения объектов на плоскости, получаемые путем пересечения плоскости с объектом.
Проекции могут быть выполнены относительно различных осей и плоскостей. Одна из таких осей — это ось z. Проекция прямой относительно оси z является двумерным отображением прямой на плоскость, получаемым путем отсечения всех координат, кроме значений по оси z.
Для получения проекции прямой относительно оси z, нужно учесть, что координаты точки на плоскости z будут равны координатам точки прямой на оси z. Остальные координаты точек прямой зануляются.
Проекции прямой относительно оси z часто используются в задачах компьютерной графики, когда необходимо рассматривать только одну из размерностей объекта. Например, для получения двухмерного изображения трехмерной модели.
Зависимость проекций от смещения прямой по оси z
Смещение прямой по оси z приводит к изменению координат ее точек в трехмерном пространстве. Также происходит изменение угла между прямой и плоскостью xy, что влияет на ее проекцию на эту плоскость.
При движении прямой по оси z, ее проекция на плоскость xy может сжиматься или расширяться в зависимости от направления смещения. Если прямая движется вдоль оси z направление от нас, то ее проекция на плоскость xy будет увеличиваться. Если же прямая движется в направлении к нам, то ее проекция на плоскость xy будет уменьшаться.
Также при смещении прямой по оси z происходит изменение проекции на плоскость xz. Если прямая движется вдоль оси z направление от нас, то ее проекция на плоскость xz будет смещаться вниз. Если же прямая движется в направлении к нам, то ее проекция на плоскость xz будет смещаться вверх.
Важно отметить, что параллельные прямые, смещенные по оси z, будут иметь одинаковую зависимость проекций на плоскости xy и xz. Это связано с сохранением параллельности этих прямых при смещении.
Таким образом, зависимость проекций от смещения прямой по оси z является важным свойством трехмерного пространства. При смещении прямой ее проекции на плоскости xy и xz могут сжиматься или расширяться, а также смещаться в зависимости от направления смещения.
Вопрос-ответ:
Что такое параллельность проекций прямой относительно оси z?
Параллельность проекций прямой относительно оси z означает, что прямая, находящаяся в трехмерном пространстве, проецируется на плоскости xy и xz таким образом, что ее проекции на эти плоскости являются параллельными друг другу.
Почему параллельность проекций прямой относительно оси z имеет значение?
Параллельность проекций прямой относительно оси z играет важную роль в геометрии и конструктивной графике. Она позволяет осуществлять точное отображение трехмерных объектов на плоскости, сохраняя пропорции и углы между элементами.
Как определить, являются ли проекции прямой параллельными?
Для определения параллельности проекций прямой относительно оси z необходимо сравнить углы, которые прямая и ее проекции образуют с осями координат. Если эти углы равны, то проекции будут параллельными.
Какое значение имеет параллельность проекций прямой в инженерном и архитектурном проектировании?
В инженерном и архитектурном проектировании параллельность проекций прямой играет важную роль при создании планов, разрезов и фасадов зданий. С ее помощью можно точно представить форму и размеры объектов на плоскости, что облегчает процесс проектирования.
Как использовать понятие параллельности проекций прямой в компьютерной графике?
В компьютерной графике параллельность проекций прямой используется для создания трехмерной визуализации объектов. Она позволяет установить правильное положение и углы объектов на экране, обеспечивая реалистичное отображение.
Что такое параллельность проекций прямой относительно оси z?
Параллельность проекций прямой относительно оси z означает, что если прямая параллельна оси z, то ее проекции на ортогональные плоскости xy и xz будут параллельны соответствующим осям.
Как определить параллельность проекций прямой относительно оси z?
Чтобы определить, параллельны ли проекции прямой относительно оси z, необходимо взглянуть на их направления. Если проекции параллельны соответствующим осям (например, обе проекции параллельны оси x), то можно считать, что они параллельны оси z.