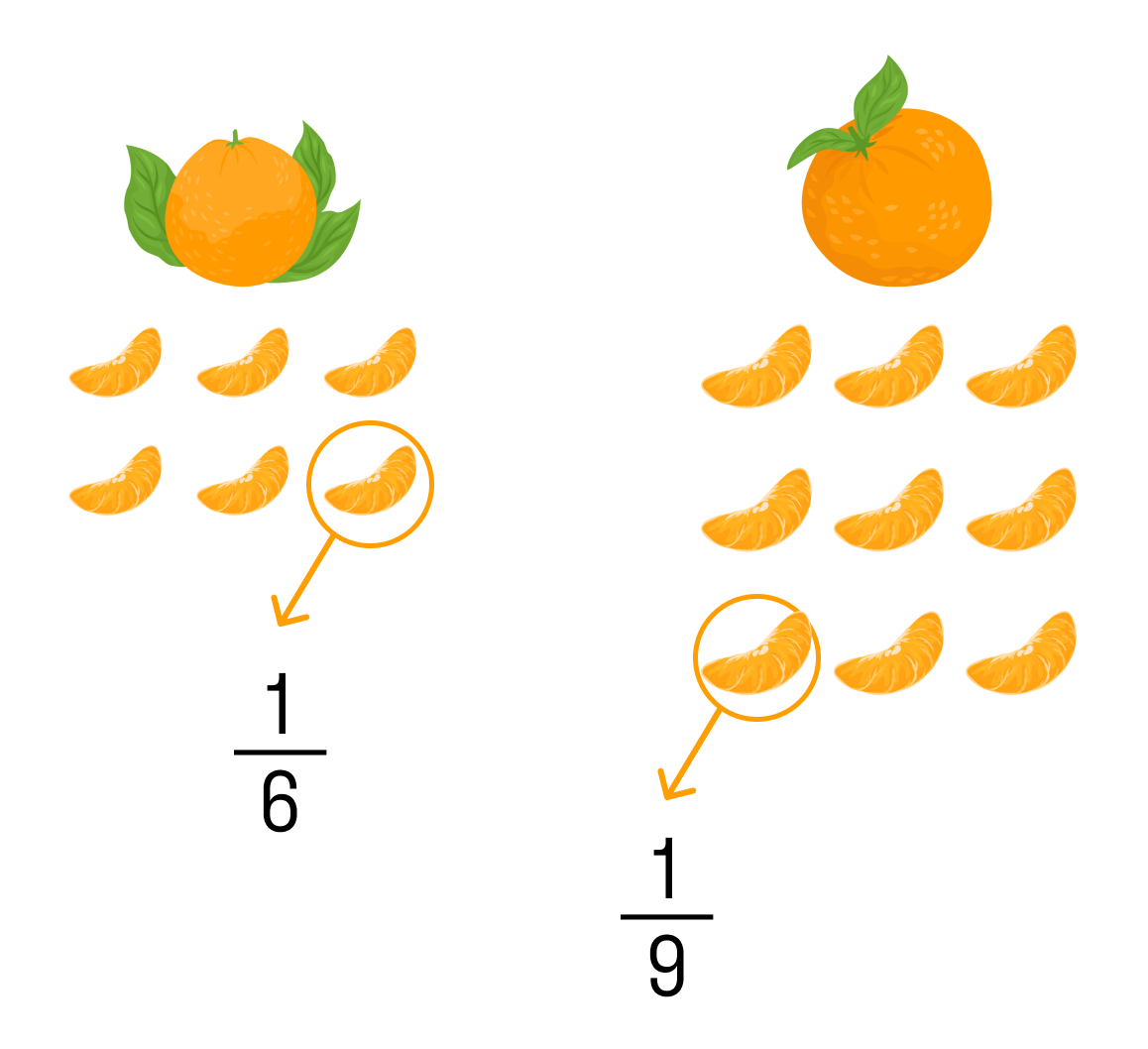
Дробь – это особый вид числа, представляющий собой отношение между двумя числами: числителем и знаменателем. Числитель указывает, сколько частей целого мы имеем, а знаменатель – на сколько частей делится целое.
В математике дроби используются для описания долей, частей целого, а также для решения разнообразных задач и уравнений. Они позволяют работать с числами, которые не являются целыми, и точно выражать дробные величины.
Примеры использования дробей можно найти во множестве ситуаций. Например, если у нас есть пицца, разделенная на 8 равных частей, а мы съели 3 из них, то мы можем записать это как дробь 3/8 – мы съели три восьмых пиццы. Аналогично, если у нас есть бассейн, заполненный до половины, то мы можем записать это как дробь 1/2 – мы заполнили половину бассейна.
Что такое дробь
Числитель представляет собой количество долей или частей, которые мы хотим выразить, а знаменатель показывает, на сколько частей целого число мы делим.
Например, рассмотрим дробь 3/4. Здесь числитель равен 3, а знаменатель равен 4. Это означает, что мы делим целое число на 4 равные части и берем 3 из них.
Дроби широко используются в различных областях, таких как финансы, рецепты, измерения и пропорции. Они также являются важной частью математики и помогают нам решать разнообразные задачи, связанные с долей чего-либо.
Важно знать, что дроби могут быть положительными, отрицательными или нулевыми, и могут иметь разное значения в зависимости от контекста, в котором они используются.
Определение дроби в математике
Дроби широко используются в математике и в реальной жизни. Например, при делении пиццы на равные части мы можем использовать дроби для определения, сколько частей от пиццы мы берем. Дроби также используются при работе с отношениями и процентами. Например, если мы хотим выразить, что у нас есть 3 равные доли от целого, мы можем использовать дробь 3/5.
Например:
В дроби 3/4 число 3 является числителем, а число 4 — знаменателем. Это означает, что мы берем 3 части от целого, которое разделено на 4 равных доли.
Также дроби могут быть положительными или отрицательными. Если числитель и знаменатель имеют одинаковый знак, дробь положительная. Если числитель и знаменатель имеют противоположные знаки, дробь отрицательная.
Использование дробей позволяет нам работать с более точными представлениями и числами, которые не могут быть представлены целыми числами. Они позволяют нам учесть доли и детали, которые могут быть важными в различных ситуациях.
Основные понятия о дробях
Основные элементы дроби:
- Числитель — верхняя часть дроби, которая указывает на количество частей.
- Знаменатель — нижняя часть дроби, которая указывает на количество равных частей, на которые разделено целое.
Формат записи дроби: числитель/знаменатель. Например, дробь 2/3 означает, что целое число разделено на 3 равные части и выбраны 2 из них.
Основные операции с дробями:
- Сложение: для сложения дробей необходимо иметь одинаковый знаменатель, после чего складываются числители и сохраняется знаменатель.
- Вычитание: аналогично сложению, необходимо иметь одинаковый знаменатель, после чего вычитается один числитель из другого и сохраняется знаменатель.
- Умножение: числители и знаменатели дробей умножаются между собой.
- Деление: для деления дробей необходимо первую дробь умножить на обратную второй дроби.
Дроби могут быть представлены в разных формах, например, правильные, неправильные, смешанные дроби или десятичные дроби. Использование дробей широко распространено в различных областях, таких как финансы, наука, инженерия и многое другое.
Десятичная дробь и обыкновенная дробь
Обыкновенные дроби представляются в виде двух чисел — числителя и знаменателя, записанных через дробную черту. Числитель указывает, сколько раз часть целого числа присутствует в дроби, а знаменатель определяет количество равных частей, на которые делится целое число. Например, в дроби 1/2, числитель равен 1, а знаменатель равен 2, что означает, что дробь представляет половину целого числа.
Десятичные дроби, с другой стороны, представляются в формате десятичной системы счисления, что означает, что они имеют цифры после запятой. Целая часть числа располагается перед запятой, а десятичная часть — после запятой. Например, в десятичной дроби 0,75, цифра 7 перед запятой является целой частью, а 5 после запятой — десятичной частью, что означает, что дробь представляет 75 сотых часть целого числа.
Конвертация между обыкновенными и десятичными дробями возможна с помощью различных методов. Например, обыкновенные дроби можно преобразовать в десятичные, разделив числитель на знаменатель. Десятичные дроби, в свою очередь, могут быть представлены в виде обыкновенных дробей, путем записи цифр до и после запятой в соответствующих числителе и знаменателе.
Числитель и знаменатель дроби
Числитель и знаменатель могут быть целыми или десятичными числами. Например, в дроби 3/4, числитель равен 3, а знаменатель равен 4. Это означает, что дробь представляет 3 части от целого, которое было разделено на 4 равные части.
Числитель и знаменатель могут иметь различные значения и могут быть отрицательными. Например, в дроби -2/5, числитель равен -2, а знаменатель равен 5. Здесь дробь представляет -2 части от целого, который был разделен на 5 равных частей.
Числитель и знаменатель могут также быть переменными или алгебраическими выражениями. Например, в дроби (x + 2)/(y — 1), числитель представляет собой сумму переменной x и числа 2, а знаменатель представляет собой разность переменной y и числа 1.
Числитель и знаменатель дроби определяют ее значением и помогают в вычислениях с дробями, такими как сложение, вычитание, умножение и деление.
Примеры использования дробей в повседневной жизни
Одним из основных примеров использования дробей является работа с деньгами. Когда мы покупаем что-то в магазине, цены на товары обычно указываются в дробной форме, например, 4,99 доллара. В таком случае, мы можем представить эту цену в виде десятичной дроби 4,99 или в виде обыкновенной дроби 4 99/100.
Дроби также используются при расчетах рецептов в кулинарии. Если в рецепте указаны полфунта муки или треть стакана сахара, то нам необходимо применить знания о дробях, чтобы правильно отмерить нужное количество ингредиентов.
Дроби применяются также в строительстве и ремонте. При предварительном рассчете материалов, таких как плитка, нам необходимо знать количество плиток на квадратный метр или на конкретную поверхность. Эти данные часто указываются в виде обыкновенных дробей, и мы должны уметь правильно использовать их, чтобы выбрать нужное количество материалов.
В финансовой сфере дроби используются для представления процентных ставок, например, 5/100 или 0,05 означает 5 процентов. Когда мы считаем проценты, дроби помогают нам определить конкретную сумму, например, сколько мы заработаем на вкладе после определенного срока.
Дроби также применяются в спорте и измерениях. Например, в беге на длинные дистанции время может быть представлено в виде десятичной дроби, например, 2,5 минуты. В то же время, дроби используются для измерения длины поля, например, 1/3 километра.
Короче говоря, дроби широко применяются в повседневной жизни и помогают нам справляться с разнообразными задачами, связанными с измерением, расчетами и представлением чисел.
Дроби в рецептах и кулинарии
Дроби играют важную роль в кулинарии и рецептах, помогая определить не только необходимые пропорции ингредиентов, но и объемы, веса и времена приготовления.
Одним из распространенных примеров использования дробей в рецептах является указание нескольких долей самой мелкой единицы измерения, такой как чайная ложка или столовая ложка. Например, рецепт может требовать «1 ½ чайной ложки соли» или «2 ¼ столовых ложки сахара». В этом случае дробные числа помогают точно измерить нужное количество ингредиента.
Дробные числа также используются для обозначения времени приготовления. Например, рецепт может указывать «1 ½ часа» или «45 минут». Это дает ясное представление о продолжительности приготовления блюда.
Кроме того, дроби могут быть использованы для определения объемов и весов ингредиентов. Например, рецепт может требовать «¼ чашки молока» или «½ килограмма муки». Здесь дроби помогают определить точные пропорции для достижения нужного результата.
| Ингредиент | Количество |
|---|---|
| Мука | 2 ½ стакана |
| Сахар | 1 ⅓ стакана |
| Молоко | ¾ стакана |
Выше приведена таблица с примером рецепта, где дробные числа используются для определения количества каждого ингредиента. Это помогает приготовить блюдо согласно рецепту и достичь желаемого вкуса и текстуры.
Таким образом, дроби играют важную роль в рецептах и кулинарии, помогая определить пропорции, объемы, веса и времена приготовления. Правильное использование дробей помогает добиться желаемого результата и создать вкусные блюда.
Пример: рецепт торта с использованием дробей
Дроби широко используются в кулинарии для измерения и смешивания ингредиентов. Давайте рассмотрим пример рецепта торта с использованием дробей.
Ингредиенты:
- 1 1/2 чашки муки
- 1/2 чашки сахара
- 1/4 чашки масла
- 2 яйца
- 1/2 стакана молока
- 1 чайная ложка разрыхлителя
- 1/2 чайной ложки ванильного экстракта
- 1/4 чайной ложки соли
Инструкции:
- Нагрейте духовку до 180 градусов.
- В большой миске смешайте муку, сахар, разрыхлитель и соль.
- Добавьте масло, яйца, молоко и ванильный экстракт в миску с сухими ингредиентами.
- Тщательно перемешайте все ингредиенты до получения однородного теста.
- Вылейте тесто в предварительно смазанную форму для выпечки.
- Поставьте форму в разогретую духовку и выпекайте торт в течение 30 минут или до золотисто-коричневого цвета.
- Извлеките торт из духовки и дайте ему остыть перед сервировкой.
Теперь у вас есть пример простого рецепта торта, в котором использованы дроби для измерения ингредиентов. Попробуйте свои силы и наслаждайтесь вкусным результатом!
Вопрос-ответ:
Что такое дробь?
Дробь — это числовой объект, представляющий отношение одного числа (числителя) к другому (знаменателю) через дробную черту. Например, 3/4.
Какие бывают типы дробей?
Существует два основных типа дробей: обыкновенные и десятичные. Обыкновенные дроби представлены в виде числителя и знаменателя, а десятичные дроби имеют бесконечную или конечную последовательность десятичных цифр после запятой.
Как происходит сложение дробей?
Для сложения дробей необходимо иметь общий знаменатель. Сначала знаменатели у обоих дробей приводятся к общему знаменателю, затем числители складываются. Результат может быть сокращен до несократимой дроби.
Как умножаются дроби?
Для умножения дробей перемножаются числители и знаменатели. Затем полученные числитель и знаменатель могут быть сокращены до несократимой дроби.
Как применяются дроби в реальной жизни?
Дроби находят широкое применение в различных сферах жизни: в кулинарии (рецепты), финансах (расчеты процентов), спорте (измерение времени и расстояния), строительстве (измерение размеров и объемов) и т.д.