Какой угол называется острым прямым тупым развернутым

В геометрии есть много типов углов, и каждый имеет свое название. Один из основных параметров, определяющих угол, — это его величина. Угол считается острым, если его величина меньше 90 градусов. Такой угол обычно обозначают символом «∠«. Например, угол ABC представляет собой острый угол, так как его величина составляет менее 90 градусов.

Прямой угол, в свою очередь, равен 90 градусам. Такой угол можно увидеть на пересечении двух перпендикулярных линий, где одна из линий горизонтальна, а вторая — вертикальна. Правильное обозначение прямого угла — «∟«. Например, угол DEF — это прямой угол, так как он составляет 90 градусов.

Если угол больше 90 градусов, то он называется тупым углом. Обычно он обозначается также символом «∠«. Например, угол GHI является тупым углом, так как его величина составляет более 90 градусов.

Развернутый угол имеет величину 180 градусов и является полным оборотом. Такой угол обычно обозначается через двойной символ «∡«. Например, угол JKL представляет собой развернутый угол, так как его величина составляет 180 градусов.

Содержание

Острые углы в геометрии

Острые углы обладают рядом основных свойств:

Острые углы всегда меньше прямого угла (равного 90 градусов).
Сумма двух острых углов всегда меньше 180 градусов (сумма всех углов треугольника).
Острые углы могут быть измерены с использованием градусов или радианов.
Острые углы могут быть равными или неравными друг другу в зависимости от их величины.

Острые углы широко используются в различных областях, таких как астрономия, физика, геодезия и строительство. Понимание свойств и измерение острых углов позволяет решать разнообразные задачи, связанные с изучением пространства и формы объектов.

Острые углы: определение и свойства

Острый угол

Острый угол – это угол, значение которого меньше 90 градусов. По определению, острый угол всегда меньше прямого угла и тупого угла.

Свойства острых углов

Острый угол всегда меньше прямого угла и тупого угла.
Сумма двух острых углов всегда равна прямому углу (90 градусов).
Острый угол может быть измерен в градусах, радианах или градах.
Острый угол может иметь разную величину, от 0 до 90 градусов.
В треугольнике все углы острые, если сумма углов треугольника равна 180 градусов.

Острые углы играют важную роль в геометрии и описывают различные свойства и отношения между линиями и фигурами. Знание острых углов помогает решать задачи и анализировать геометрические фигуры.

Прямые углы: свойства и особенности

Прямой угол

Прямой угол – это угол, размер которого равен 90 градусам или $\frac{\pi}{2}$ радиан. Он имеет особое положение, так как является наиболее распространенным и хорошо изученным углом в геометрии.

Прямой угол имеет несколько важных свойств и особенностей:

Прямой угол может быть образован двумя перпендикулярными прямыми, то есть такими, которые образуют прямой угол друг с другом.
У прямого угла вершина лежит на окружности, центр которой совпадает с концом лучей угла.
Всякий угол, меньший прямого угла, называется острым углом.
Угол, больший прямого угла, называется тупым углом.
Прямой угол может быть также развернутым углом, когда лучи угла лежат на одной прямой, но направлены в разные стороны.

Острый, прямой и тупой углы

Острый угол – это угол, размер которого меньше 90 градусов или $\frac{\pi}{2}$ радиан. Он имеет острое призвание, так как его ребра сходятся в небольшой точке.

Тупой угол – это угол, размер которого больше 90 градусов или $\frac{\pi}{2}$ радиан. Он также имеет свои особенности и может быть образован двумя разнонаправленными лучами.

Развернутый угол – это угол, размер которого равен 180 градусам или $\pi$ радиан. Он образуется, когда лучи угла лежат на одной прямой и направлены в разные стороны.

Тупые углы: классификация и примеры

Тупой угол – это угол, который имеет величину больше 90 градусов и меньше 180 градусов. Возьмем, например, две стороны стола, которые образуют угол более 90 градусов. Такой угол можно считать тупым.

В природе также можно встретить примеры тупых углов. Например, угол между двумя касательными к окружности, которые пересекаются вне этой окружности, будет тупым. Еще одним примером является угол между двумя наклонными поверхностями, который имеет величину более 90 градусов.

Тупые углы встречаются не только в геометрии, но и в других областях. Например, тупой угол можно наблюдать на планете Земля в местах, где линия горизонта формируется из-за изгиба поверхности.

Определение и примеры тупых углов помогают лучше понять и классифицировать различные углы. Знание этих понятий может быть полезно как в школе для успешного изучения геометрии, так и в повседневной жизни для лучшего понимания окружающего мира.

Развернутые углы: определение и использование

Развернутые углы имеют важное применение в геометрии и находятся во многих ежедневных ситуациях. Они широко используются в картографии для измерения и построения углов на картах и планах.

В астрономии развернутые углы используются для измерения величины и расстояний между звездами и планетами. Они также используются в навигации для определения направления движения и маршрута.

Развернутые углы часто встречаются в повседневной жизни. Например, при игре в бильярд или гольф, игроки используют развернутые углы для определения траектории шара или удара.

Еще одним примером использования развернутых углов является строительство и архитектура. Архитекторы и инженеры используют эти углы при проектировании зданий, мостов и других сооружений.

Развернутые углы также широко применяются в науке, например, в физике, математике и геологии. Они используются для измерения и анализа различных явлений и процессов.

Углы, сумма которых равна 180 градусов

Углы, сумма которых равна 180 градусов, называются смежными. Это означает, что они располагаются на одной прямой. Смежные углы дополняют друг друга и образуют прямую линию.

Один из примеров смежных углов — это острый и тупой углы. Острый угол имеет меньшую меру, чем 90 градусов, тогда как тупой угол имеет меру больше 90 градусов, но меньше 180 градусов.

Также, два прямых угла считаются смежными, так как их сумма равна 180 градусов. Прямой угол имеет меру 90 градусов и делит окружность на две равные части.

Сумма всех углов в треугольнике также равна 180 градусов. В треугольнике есть три угла, и их сумма всегда будет равна прямому углу.

Изучение углов, сумма которых равна 180 градусов, важно для геометрии и решения задач, связанных с построением фигур и определением их свойств. Это позволяет нам лучше понимать структуру и форму нашего мира.

Как определить острый угол

В декартовой системе координат, острый угол находится между осью абсцисс (ось x) и линией, которая проходит через точку, образующую угол, и начало координат.

Способы определения острого угла:

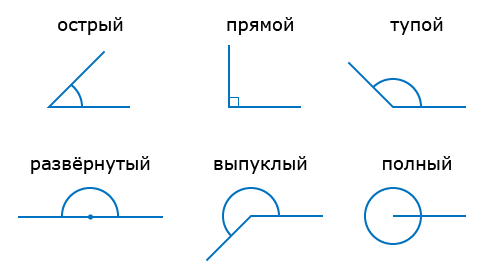
1. Используйте геометрический инструментарий, например, циркуль и линейку.

Сначала нарисуйте ось абсцисс (ось x) на листе бумаги, а затем проведите линию, начинающуюся от начала координат и проходящую через точку, образующую угол.

Затем, при помощи циркуля, измерьте угол между этой линией и осью абсцисс. Если измеренный угол меньше 90 градусов и больше 0 градусов, то это острый угол.

2. Используйте тригонометрические функции, такие как синус, косинус и тангенс.

Если угол меньше 90 градусов, то синус угла будет положительным числом, а косинус и тангенс будут принимать значения от 0 до 1.

Также можно использовать таблицы значений синуса, косинуса и тангенса, чтобы определить, является ли угол острым.

3. Используйте геометрические свойства острого угла. Например, в остром угле противолежащая сторона всегда меньше гипотенузы (самой длинной стороны), а сумма двух катетов всегда больше гипотенузы.

Если эти условия выполняются, то угол является острым.

Практическое применение острых, прямых, тупых и развернутых углов

Знание острых, прямых, тупых и развернутых углов имеет практическое применение во многих сферах нашей жизни. Рассмотрим несколько примеров:

1. Архитектура и строительство. При проектировании зданий и сооружений необходимо учитывать углы, чтобы обеспечить их прочность и устойчивость. Знание острых углов позволяет определить оптимальные габариты и форму конструкций.

2. Геометрия и математика. Углы являются одним из основных элементов геометрических фигур и фигур в пространстве. Они используются для решения задач по вычислению площадей, объемов, длин и других характеристик фигур.

3. Навигация и картография. Углы используются для определения направления и ориентации на местности. Углы на карте помогают определить курс движения, расстояния между объектами и позволяют строить маршруты.

4. Инженерное дело. В различных инженерных отраслях, таких как машиностроение, электротехника, химическое производство и другие, углы используются для расчета и определения параметров конструкций и систем.

5. Измерения и метрология. Углы используются при измерении различных величин и характеристик предметов. Например, при определении угла обзора камеры, угла отклонения изделий при проверке на соответствие стандартам и т.д.

Важно знать и понимать углы, так как они помогают решать разнообразные практические задачи и ситуации в различных областях нашей жизни.