Что называют косинусом угла а где 0 a 180

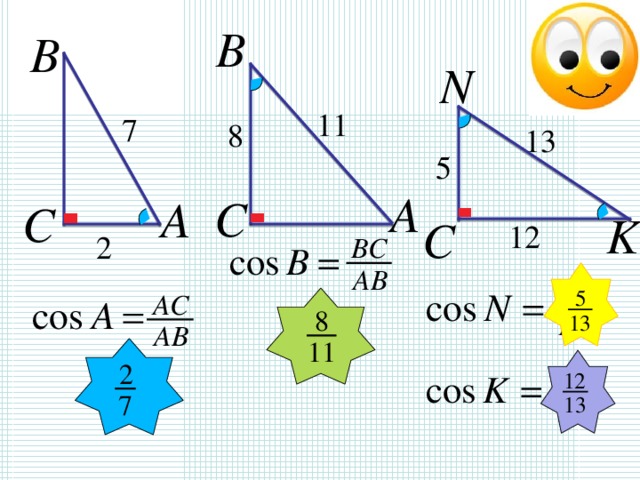
Косинус — одна из основных тригонометрических функций, которая определяется отношением длины прилежащего катета к гипотенузе прямоугольного треугольника. В математике косинус угла α обычно обозначается как cos(α) или cos α.

Угол α измеряется в градусах и его значения лежат в интервале от 0 до 180. Нулевое значение косинуса (cos(0) или cos 0) равно 1, так как в случае, когда α = 0, прилежащий катет равен гипотенузе и их отношение равно единице.

Когда α увеличивается до 90 градусов, прилежащий катет принимает значение 0, а гипотенуза остается существовать, что приводит к нулевому значению косинуса (cos(90) или cos 90). Это можно объяснить тем, что при α = 90 прямоугольный треугольник превращается в прямую линию, и отношение прилежащего катета к гипотенузе становится нулевым.

Когда α достигает значения 180 градусов, прилежащий катет снова равен гипотенузе, но в этом случае прилежащий катет имеет противоположное направление по отношению к началу координат. Следовательно, косинус 180 градусов (cos(180) или cos 180) снова равен 1.

Содержание

Косинус угла: определение, свойства и применение

Определение

Косинусом угла α называется отношение прилежащего катета к гипотенузе прямоугольного треугольника.

Косинус угла α обозначается как cos(α).

Значение косинуса угла может быть от -1 до 1 включительно. Если угол равен 0 или 180 градусов, то косинус угла равен 1. Если угол равен 90 градусов, то косинус угла равен 0. Если угол равен 270 градусов, то косинус угла равен 0.

Свойства

Основные свойства косинуса угла:

Косинус угла α равен косинусу его дополнения: cos(α) = cos(180 — α).
Косинус угла α является четной функцией: cos(-α) = cos(α).
Косинус угла α является периодической функцией с периодом 360 градусов: cos(α + 360k) = cos(α) для любого целого числа k.

Применение

Косинус угла широко применяется в преобразовании координат, моделировании движения и волн, анализе сигналов, решении уравнений и других областях.

Он также находит применение в геометрии и трехмерной графике для определения расстояний и углов между объектами.

Кроме того, косинус угла находит применение в физических законах, таких как закон Гука, закон Кулона и закон Уиттенера.

В целом, косинус угла играет важную роль в математике и науке, позволяя нам анализировать и понимать множество явлений и величин.

Что такое косинус угла?

Косинус угла α обозначается как cos(α) и может принимать значения от -1 до 1. Если значение косинуса положительное, то это означает, что угол α находится в первой или в четвертой четверти. Если значение косинуса отрицательное, то угол α находится во второй или в третьей четверти.

Значения косинуса угла α можно найти в специальных таблицах или с помощью калькулятора, но также можно приближенно вычислить с помощью формулы или программного кода.

Косинус угла широко применяется в различных областях науки и техники, включая физику, математику, геометрию, механику, электронику и программирование. Он используется для решения задач, связанных с расчетами траекторий движения, определения углов между векторами, нахождения косинусного сходства в анализе данных и многих других приложениях.

Как вычислить значение косинуса угла?

Определите длины сторон треугольника, содержащего данный угол, с помощью известных значений или измерений.
Выберите сторону треугольника, которая является прилежащим катетом угла, значение косинуса которого вы хотите вычислить.
Определите значение гипотенузы треугольника, если оно неизвестно, с помощью известных значений сторон или используя теорему Пифагора.
Вычислите значение косинуса угла, разделив длину прилежащего катета на длину гипотенузы.

Заметим, что значение косинуса угла всегда находится в диапазоне от -1 до 1, где -1 соответствует углу 180 градусов, а 1 — углу 0 градусов.

Свойства косинуса угла

Свойства косинуса угла:

Свойство	Формула
Периодичность	cos(a + 2π) = cos(a)
Четность	cos(-a) = cos(a)
Значение на границе	cos(0) = 1, cos(π) = -1
Косинус суммы углов	cos(a + b) = cos(a) * cos(b) — sin(a) * sin(b)
Косинус разности углов	cos(a — b) = cos(a) * cos(b) + sin(a) * sin(b)
Косинус половинного угла	cos(a/2) = ±√((1 + cos(a))/2)

Используя эти свойства, можно вычислить значение косинуса угла и проводить различные тригонометрические преобразования.

Косинус углов от 0 до 90 градусов

В промежутке от 0 до 90 градусов косинус угла имеет свойства:

1. Косинус угла 0 градусов

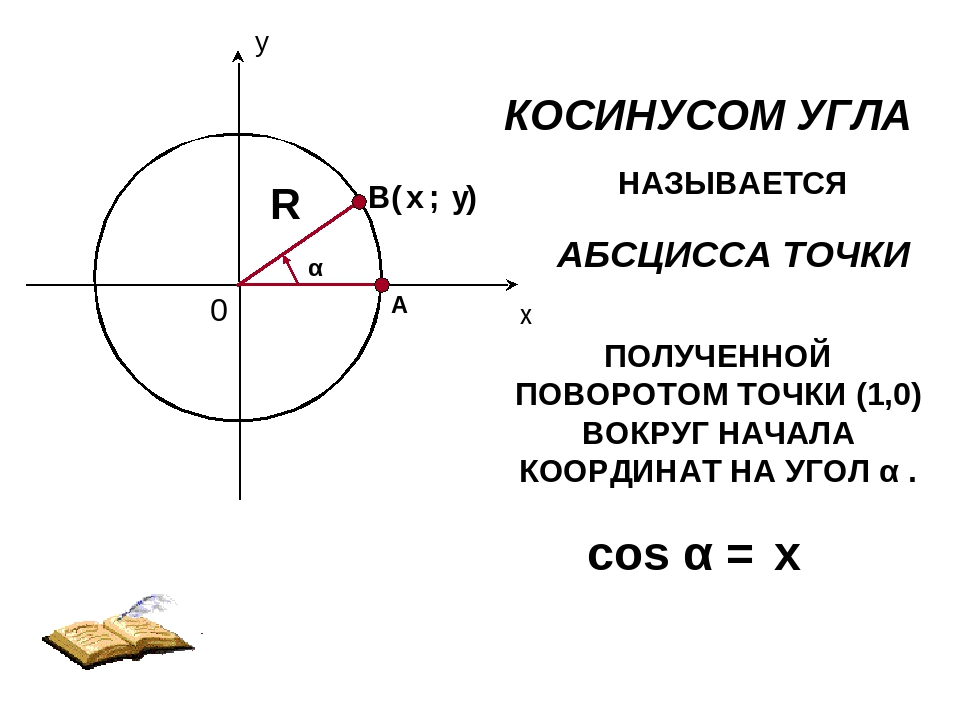
Когда угол равен 0 градусов, косинус угла равен 1. Это означает, что соответствующая точка лежит на оси x и имеет координаты (1, 0) на единичной окружности.

2. Косинус угла 90 градусов

Когда угол равен 90 градусов, косинус угла равен 0. В этом случае соответствующая точка лежит на оси y и имеет координаты (0, 1) на единичной окружности.

Таким образом, при увеличении угла в промежутке от 0 до 90 градусов, значение косинуса уменьшается от 1 до 0.

Косинус углов от 90 до 180 градусов

Когда речь идет о косинусе угла от 90 до 180 градусов, он будет отрицательным числом в диапазоне от -1 до 0. Это происходит потому, что косинус угла от 90 до 180 градусов соответствует углам, которые находятся во втором и третьем квадрантах геометрической плоскости. В этих квадрантах косинус угла будет отрицательным.

Например, косинус 135 градусов равен -0.7071. Это значит, что сторона противолежащая углу в прямоугольном треугольнике имеет длину, равную 0.7071 от длины гипотенузы, при условии, что гипотенуза равна 1.

Отметим, что вместе с косинусом второго и третьего квадранта, синус будет также отрицательным числом, а тангенс и котангенс будут положительными.

Косинус углов от 180 до 270 градусов

Когда мы говорим о косинусе угла от 180 до 270 градусов, имеем в виду углы, которые находятся в третьем и четвертом квадрантах на координатной плоскости. В этих квадрантах значение косинуса отрицательно, так как среди основных тригонометрических функций косинус определяется как отношение прилежащего катета к гипотенузе прямоугольного треугольника.

В третьем квадранте, углы находятся между 180 и 270 градусами. Значение косинуса в этом квадранте убывает от 0 до -1 по мере увеличения угла. На графике косинуса мы можем наблюдать, что в третьем квадранте косинус принимает значения в диапазоне от 0 до -1.

В четвертом квадранте, углы находятся между 270 и 360 градусами. Значение косинуса в этом квадранте также убывает от 0 до -1 по мере увеличения угла. График косинуса в четвертом квадранте также показывает, что косинус принимает значения в диапазоне от 0 до -1.

Таким образом, косинус углов от 180 до 270 градусов равен от 0 до -1.

Косинус углов от 270 до 360 градусов

Когда угол находится в диапазоне от 270 до 360 градусов, косинус угла становится отрицательным. Данный диапазон соответствует четвертому квадранту на единичной окружности.

В четвертом квадранте, x-координата точек на единичной окружности от -1 до 0, а y-координата от -1 до 0. Также, косинус угла равен значению x-координаты точки на единичной окружности.

Таким образом, косинус углов от 270 до 360 градусов принимает значения от -1 до 0. Например, косинус угла 270 градусов равен -1, а косинус угла 360 градусов равен 0.

Косинус угла 360 градусов является особенным значением, так как он совпадает с косинусом угла 0 градусов. Это связано с периодичностью тригонометрических функций.

Применение косинуса угла в математике и физике

Математика

В математике косинус угла используется для решения геометрических задач, а также при исследовании и построении графиков функций. Косинус угла является одной из тригонометрических функций, которая широко применяется при решении треугольных задач.

Также косинус угла находит применение при решении задач дифференциального и интегрального исчисления, в теории вероятностей и статистике и в других разделах математики.

Физика

В физике косинус угла применяется для расчёта и анализа различных векторных и скалярных величин. Он позволяет определить значительные характеристики, такие как направление, скорость, ускорение и др., а также силы и работу. Косинус угла широко используется в механике, астрономии, электричестве и многих других областях физики.

Применение косинуса угла в математике и физике позволяет упростить сложные расчёты и моделирование различных физических явлений. Знание свойств и применения косинуса угла является необходимым для решения широкого круга задач в этих науках.

Вопрос-ответ:

Что такое косинус угла?

Косинус угла — это тригонометрическая функция, определенная для любого угла с помощью отношения прилежащего катета к гипотенузе прямоугольного треугольника.