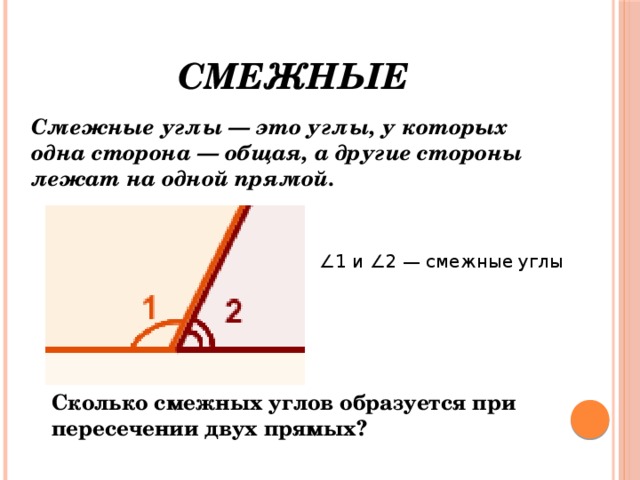
Смежные углы — это два угла, которые имеют общую вершину, общую сторону и не пересекаются внутри себя. Они играют важную роль в геометрии и широко используются при решении различных задач. Для определения смежных углов необходимо учесть несколько правил и хорошо представлять себе геометрическую форму.
Существует несколько способов определения и проверки смежных углов. Один из них — визуальный метод. Визуально смежные углы можно определить, рассматривая геометрическую фигуру или конструкцию. Если два угла имеют общую вершину и общую сторону, и при этом не пересекаются друг с другом, то они являются смежными углами.
Еще один способ определения смежных углов — аналитический метод. Для его применения необходимо знание координат и формул аналитической геометрии. Аналитические методы позволяют вычислить значение смежных углов, а также провести различные операции с ними, например, сравнение или сложение.
Определение смежных углов
Для определения смежных углов необходимо найти две прямые линии или поперечную плоскость, при пересечении которых образуются углы. Затем нужно установить, что эти углы имеют одну общую сторону, находятся в той же плоскости и примыкают друг к другу без промежуточных углов.
Смежные углы важны для изучения геометрии и решения различных геометрических задач. Зная их свойства и особенности, можно более точно определить взаимное расположение углов и линий, а также использовать их для нахождения неизвестных значений углов в различных геометрических фигурах.
Что такое смежные углы и их основное определение
Обычно смежные углы образуются при пересечении двух прямых, при этом два угла с общей стороной и находящиеся по разные стороны от этой стороны являются смежными углами. Важно отметить, что их сумма равна 180 градусам.
Смежные углы встречаются не только в геометрии, но и в повседневной жизни. Например, когда два предмета или поверхности пересекаются и образуют угол, этот угол и его соседние углы будут смежными углами.
Знание о смежных углах важно при решении задач на геометрию и в областях, где требуется анализ углов и пространственных форм. Изучение смежных углов помогает лучше понять и изучить геометрические свойства и закономерности.
Углы, имеющие общую вершину и сторону
Важно помнить, что смежные углы могут быть как смежными дополнительными, так и смежными совпадающими. Смежные дополнительные углы составляют сумму 180 градусов, в то время как смежные совпадающие углы имеют одинаковую меру и являются парой.
Например, в прямоугольнике два смежных угла с вершиной и общей стороной называются смежными совпадающими углами, так как они оба равны 90 градусам. В треугольнике два смежных угла с вершиной и общей стороной называются смежными дополнительными углами, так как их сумма равна 180 градусам.
Смежные углы играют важную роль в геометрии, так как они позволяют определить различные свойства и отношения между углами в фигурах.
Углы, сумма которых составляет 180 градусов
Существуют два угла, сумма которых равна 180 градусов. Такие углы называются смежными углами. Смежные углы образуются двумя пересекающимися прямыми линиями и имеют общую вершину.
Для того чтобы определить, являются ли два угла смежными и их сумма равна 180 градусов, необходимо проверить несколько условий:
- Пересекают ли две прямые линии друг друга. Если прямые параллельны, то их углы не будут смежными.
- Если углы образуются двумя пересекающимися прямыми линиями, то их сумма всегда будет равна 180 градусов.
Смежные углы важны при изучении геометрии и применяются в различных математических задачах. Например, зная значение одного угла, можно найти значение другого смежного угла, или наоборот.
При работе с смежными углами также важно учитывать их тип. Углы могут быть остроугольными (меньше 90 градусов), прямыми (90 градусов) или тупыми (больше 90 градусов).
Изучение смежных углов позволяет более глубоко понять и применять геометрические законы и теоремы.
Как определить смежные углы
1. По определению: Если два угла имеют общую сторону и вершину, то они являются смежными углами.
2. По геометрическому изображению: При наличии изображения фигуры или геометрической конструкции, смежные углы можно определить визуально. Найдите два угла, имеющих общую сторону и вершину, а затем убедитесь, что они образуют линию.
3. С помощью угловой меры: Если у вас есть инструмент для измерения углов, например, угломер или градусник, вы можете определить смежные углы, измерив их величину. Смежные углы всегда имеют одинаковую меру.
4. С использованием геометрических свойств: Известны несколько свойств смежных углов, которые помогают их определить. Например, сумма смежных углов всегда равна 180 градусам. Если у вас есть информация о других углах или сторонах фигуры, то вы можете использовать эти свойства для определения смежных углов.
Важно помнить, что смежные углы встречаются в разных геометрических фигурах и конструкциях. Их понимание и умение определять и использовать эти углы являются важными навыками в геометрии и других областях, где применяются углы.
Способы определения смежных углов
- По определению. Смежные углы — это углы, которые находятся рядом друг с другом и имеют одну общую сторону. При этом их вершины лежат на разных сторонах этой общей стороны.
- По изображению. Если на чертеже или диаграмме видны два угла, которые имеют одну общую сторону и вершину, то они являются смежными углами.
- По свойствам углов. Если известно, что сумма двух углов равна 180 градусам, а эти углы имеют одну общую сторону и вершину, то они являются смежными углами.
- По геометрическим фигурам. В некоторых геометрических фигурах, таких как треугольник или параллелограмм, можно определить смежные углы по особенностям фигуры.
Определив смежные углы, можно использовать их свойства для решения различных геометрических задач. Например, если известно, что два угла являются смежными и их сумма равна 90 градусам, то это означает, что эти углы являются смежными и дополнительными.
Используя геометрический инструментарий
Гониометр — это инструмент, который используется для измерения и построения углов. С помощью гониометра можно определить смежные углы путем измерения их величины.
Для определения смежных углов сначала необходимо выбрать одну сторону угла и нанести ее на лист бумаги или другую поверхность с помощью линейки и карандаша. Затем, с помощью гониометра, измерьте угол между этой стороной и каждой из остальных сторон.
Смежные углы обладают специфической особенностью: сумма их величин равна 180 градусов. Это означает, что если вы сможете измерить два угла и их сумма будет равна 180 градусов, значит, это смежные углы.
Другим доступным инструментом для работы с смежными углами является циркуль. Циркулем можно провести дугу угла, а затем измерить эту дугу с помощью линейки или гониометра. Также циркулем можно построить параллельные прямые, в том числе и смежные углы.
Важно помнить, что смежные углы образуются двумя пересекающимися прямыми линиями и имеют общую вершину. Определение и работа с смежными углами может быть полезным для решения геометрических задач и заданий связанных с углами и фигурами.
Использование геометрического инструментария может быть эффективным и удобным способом для определения и работы с смежными углами.
Анализируя геометрические фигуры, в которых углы расположены
Смежные углы могут быть расположены в различных геометрических фигурах, таких как треугольники, квадраты, прямоугольники и многоугольники. Анализ этих фигур позволяет нам определить, как углы расположены и взаимосвязаны внутри них.
Треугольники
В треугольниках смежные углы лежат на двух сторонах и имеют одну общую вершину. Они могут быть либо смежными в пределах одной стороны, либо смежными на разных сторонах треугольника. Это позволяет нам классифицировать треугольники с учетом взаимного положения и типа смежных углов.
Квадраты и прямоугольники
В квадратах и прямоугольниках смежные углы всегда равны и равны 90 градусам. У каждой вершины такой фигуры есть два смежных угла, расположенных горизонтально или вертикально.
Многоугольники
В многоугольниках, у которых более трех сторон, смежные углы могут быть разнообразными и иметь разные значения. Определение и расположение смежных углов в многоугольниках зависит от их формы и количества сторон.
Анализ геометрических фигур, в которых углы расположены, позволяет нам понять, как они взаимосвязаны и каким образом можно определить меру и свойства углов внутри них. Понимание смежных углов и их расположение является важной основой для дальнейшего изучения геометрии и решения геометрических задач.
Примеры смежных углов в повседневной жизни
Смежные углы можно встретить в разных ситуациях повседневной жизни:
1. В геометрии:
Когда строим здания и многоугольники, часто встречаются смежные углы. Например, углы прилегающих стен или вершины многоугольника.
2. В дорожном движении:
При повороте транспортного средства налево или направо, водитель должен учитывать смежные углы для безопасной смены полосы.
3. В современном дизайне интерьера:
Дизайнеры используют смежные углы, чтобы создать гармоничные и пропорциональные композиции. Например, углы между стенами в комнате или мебелью.
Знание и понимание смежных углов позволяет лучше анализировать и визуализировать пространство, а также правильно планировать и размещать объекты в повседневной жизни.
Вопрос-ответ:
Как определить смежные углы?
Смежные углы — это два угла, которые имеют общую сторону и общую вершину. Если два угла имеют общую сторону и вершину, то они считаются смежными. Например, если у нас есть две прямые, пересекающиеся в точке O, и у нас есть два угла: AOB и BOC, то они будут смежными, так как у них есть общая сторона и вершина.
Что означает понятие «смежные углы»?
Смежные углы — это углы, расположенные друг возле друга и имеющие общую сторону и общую вершину. Это означает, что одна и та же сторона и вершина являются общими для двух смежных углов. Смежные углы часто встречаются в геометрии и используются в различных вычислениях.
Дайте определение смежных углов.
Смежные углы — это два угла, которые имеют общую сторону и общую вершину. Это означает, что две стороны одного угла являются продолжением двух сторон другого угла, а вершина одного угла является вершиной другого угла. Например, если у нас есть угол ABC и угол CBD, и оба угла имеют общую сторону BC и общую вершину B, то они считаются смежными углами.
Какие характеристики должны быть у углов, чтобы они считались смежными?
У углов должны быть две общие характеристики, чтобы они считались смежными: общая сторона и общая вершина. Другими словами, два угла считаются смежными, если у них есть одна и та же сторона и одна и та же вершина. Например, если у нас есть угол ABC и угол CBD, и у них есть общая сторона BC и общая вершина B, то они считаются смежными углами.
Какие особенности у смежных углов?
Смежные углы имеют несколько особенностей. Одна из них — сумма смежных углов равна 180 градусов. Это означает, что если у нас есть два смежных угла — угол A и угол B, то их сумма будет равна 180 градусов. Кроме того, смежные углы могут быть смежными вертикальными углами, что означает, что они равны друг другу. Это происходит, когда у двух углов общая вершина и стороны являются продолжением друг друга.