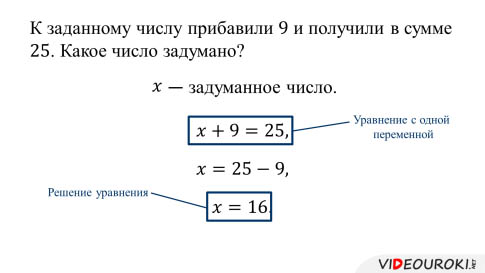
Уравнение – это математическое выражение, которое содержит один или несколько неизвестных символов, обычно обозначаемых буквами, и знак равенства. В уравнении две части разделены знаком равенства, причем каждая из них может содержать числа, операции и переменные.
Уравнение позволяет найти значения неизвестных, удовлетворяющих условию равенства. Решать уравнения – значит находить значения переменных, при которых обе части уравнения становятся равными.
Примеры уравнений в математике включают линейные, квадратные, трехчленные уравнения и другие. Например, уравнение 3x + 5 = 14 является линейным, где x – неизвестная, которую необходимо найти. Чтобы решить это уравнение, нужно найти такое значение x, при котором левая и правая части станут равными. В данном случае, x = 3.
Уравнения широко применяются в разных областях науки и техники. Они помогают решать сложные задачи и находить значения переменных в различных математических моделях. Понимание уравнений является основой для изучения алгебры и других математических дисциплин.
Что такое уравнение?
Цель решения уравнения заключается в определении значения переменной, при котором оба выражения находятся в равенстве друг с другом. Решение уравнения представляет собой поиск значения переменной, удовлетворяющего данному равенству.
Примеры уравнений:
2x + 5 = 11
x2 — 7x + 10 = 0
В первом примере уравнения, переменная x может быть найдена путем вычитания 5 из обеих сторон уравнения и затем разделения оставшегося выражения на 2. Таким образом, x равно 3.
Во втором примере уравнения, переменная x может быть найдена путем факторизации выражения или использования квадратного корня. В этом случае, x равно 2 или 5.
Уравнения широко используются в математике и в других научных дисциплинах для моделирования и решения различных проблем и задач.
Определение уравнения
Основная цель уравнения – найти значение или значения неизвестной величины, удовлетворяющих заданному условию или связи между объектами. Для этого применяются различные методы, такие как алгебраические преобразования и численные методы.
Уравнение может быть линейным или нелинейным, в зависимости от формы выражения и степени переменных. Линейные уравнения представляют собой простую линейную связь между переменными, а нелинейные уравнения могут иметь более сложную форму.
Примеры уравнений:
- Линейное уравнение: 2x + 3 = 7
- Квадратное уравнение: x^2 + 5x + 6 = 0
- Система уравнений:
- x + y = 5
- 2x — y = 3
- Тригонометрическое уравнение: sin(x) + cos(x) = 1
Уравнения играют важную роль во многих областях науки и техники, таких как физика, инженерия, экономика и т. д. Они помогают моделировать и решать различные проблемы и задачи, представляя их в математической форме.
Уравнение в математике
Уравнение в математике представляет собой выражение, содержащее неизвестную величину и знак равенства. Уравнение позволяет находить значения неизвестной величины, удовлетворяющие заданным условиям. В общем виде уравнение может быть записано следующим образом:
А + В = C
где А, В и C — это величины или выражения, а знак «+» означает операцию сложения. Неизвестная величина обычно обозначается x или у.
Примерами уравнений могут служить:
| Пример | Решение |
|---|---|
| x + 5 = 10 | x = 5 |
| 2y — 3 = 7 | y = 5 |
| 3a + 2a = 35 | a = 7 |
Решение уравнения состоит в нахождении значения неизвестной величины, при котором обе его части станут равными. В приведенных примерах значения неизвестных x, y и a равны 5, 5 и 7 соответственно.
Анализ и решение уравнений является одним из основных элементов алгебры и применяется в различных областях науки и техники.
Уравнение в физике
Одним из примеров уравнения в физике является закон сохранения энергии, который записывается в виде уравнения: Эк + Еп = const. Здесь Эк обозначает кинетическую энергию, Еп — потенциальную энергию, а const — постоянную величину.
Другим примером уравнения в физике является закон всемирного тяготения, который записывается в виде уравнения: F = G * (m1 * m2) / r^2. Здесь F обозначает силу тяготения, G — гравитационную постоянную, m1 и m2 — массы тел, а r — расстояние между ними.
Уравнения в физике могут быть представлены как аналитическими, так и дифференциальными, в зависимости от специфики задачи. Они позволяют проводить расчеты, прогнозировать поведение системы и проверять соответствие экспериментальных данных с теоретическими моделями.
Уравнение в химии
В химии уравнение представляет собой символьную запись химической реакции, которая происходит между различными веществами. Оно показывает, какие вещества вступают в реакцию (реагенты) и какие вещества получаются в результате реакции (продукты).
Уравнение в химии состоит из химических формул реагентов и продуктов, разделенных реакционной стрелкой. Каждый компонент химического уравнения представляется в виде формулы вещества, которое задается символами химических элементов и их индексами.
Примером уравнения в химии может служить уравнение реакции горения метана: CH4 + 2O2 -> CO2 + 2H2O. В этом уравнении метан (CH4) и кислород (O2) являются реагентами, а углекислый газ (CO2) и вода (H2O) — продуктами реакции.
Уравнение в химии является важным инструментом для описания химических реакций и проведения расчетов. Оно позволяет предсказать, сколько вещества будет образовываться или расходоваться в реакции, а также оценить энергетические и стехиометрические характеристики процесса.
Примеры уравнений
Вот некоторые примеры уравнений:
Пример 1: Решите уравнение: 2x + 5 = 15.
Решение: Сначала вычитаем 5 из обеих сторон: 2x + 5 — 5 = 15 — 5. Получаем 2x = 10. Затем делим обе стороны на 2: 2x/2 = 10/2. Получаем x = 5. Таким образом, решением данного уравнения является x = 5.
Пример 2: Решите уравнение: 3(x — 4) = 6x + 2.
Решение: Сначала раскрываем скобки: 3x — 12 = 6x + 2. Далее переносим все x-термы на одну сторону, а все константы на другую сторону: 3x — 6x = 2 + 12. Получаем -3x = 14. Затем делим обе стороны на -3: -3x/-3 = 14/-3. Получаем x = -14/3. Таким образом, решением данного уравнения является x = -14/3.
Пример 3: Решите квадратное уравнение: x^2 — 6x + 9 = 0.
Решение: Данное уравнение можно записать в виде (x — 3)^2 = 0, что эквивалентно (x — 3)(x — 3) = 0. Получается, что x — 3 = 0 или x — 3 = 0. Решая эти два уравнения, получаем x = 3. Таким образом, решением данного квадратного уравнения является x = 3.
Уравнения являются важным инструментом в математике и науке, и их решение может помочь нам найти решения различных проблем и задач.
Уравнения в математике
Примеры уравнений:
- 3x + 2 = 8
- 2(x + 4) = 10
- 4x^2 — 5x + 2 = 0
- sin(x) + cos(x) = 1
В математике существуют различные методы решения уравнений, такие как подстановка, факторизация, методы итерации и многие другие. Они позволяют найти все возможные значения переменной, при которых уравнение будет выполняться.
Линейное уравнение
ax + b = 0
Где a и b — это коэффициенты, а x — это переменная, которую нужно найти. Линейное уравнение имеет единственное решение, если коэффициент a не равен нулю.
Примеры линейных уравнений:
- 2x + 3 = 7
- 4x — 5 = 3x + 2
- 0.5x + 2.5 = 1.5
Решение линейного уравнения можно найти, используя различные методы, такие как подстановка, избавление от переменной или графический метод. Используя эти методы, можно определить значение переменной x, удовлетворяющее уравнению.
Вопрос-ответ:
Что такое уравнение?
Уравнение — это математическое равенство, содержащее неизвестные и знак равенства. Оно позволяет найти значения неизвестных, при которых равенство становится верным.
Какие бывают виды уравнений?
В зависимости от количества неизвестных и степени этих неизвестных, уравнения могут быть линейными, квадратными или высших степеней. Линейные уравнения содержат только одну переменную и имеют степень 1 в каждом слагаемом.
Как решить уравнение?
Для решения уравнения необходимо привести его к виду, в котором все неизвестные находятся на одной стороне знака равенства, а на другой стороне остаются только числа. Затем с помощью различных методик (исключение, подстановка, графический метод и т.д.) находятся значения неизвестных, при которых уравнение выполняется.
Можете привести пример линейного уравнения?
Конечно! Примером линейного уравнения может быть уравнение вида 2x + 3 = 7. Здесь переменная x является неизвестной, а коэффициенты 2 и 3 — известными числами. Решая это уравнение, мы найдем значение x, при котором равенство становится верным.
Какие существуют методы решения уравнений?
Для решения уравнений существует множество методик, включая алгоритмы и приемы. Некоторые из них включают метод подстановки, метод исключения, метод графического решения, методы формул и другие. Используемый метод зависит от типа и сложности уравнения.