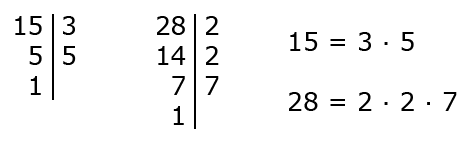
Наибольший общий делитель (НОД) двух или более чисел — это самое большое число, на которое делятся без остатка все заданные числа.
НОД имеет важное значение в различных областях математики и информатики. Он используется для упрощения дробей, решения уравнений, нахождения общих делителей, проверки простоты чисел и многих других задач.
Существует несколько способов нахождения НОД. Один из наиболее популярных методов — алгоритм Евклида. Он основан на том, что если число A делится на B без остатка, то НОД(A, B) равен B. Если B не является делителем A, то можно повторить процесс, заменив A на B и B на остаток от деления A на B. Это делается до тех пор, пока A или B не станут равными нулю. В этом случае НОД будет равен другому числу. Алгоритм Евклида позволяет быстро находить НОД даже для больших чисел.
Наибольший общий делитель (НОД): определение и применение
Для нахождения НОД двух чисел можно использовать несколько методов. Один из самых простых способов – это метод Евклида. Он основан на следующем принципе: НОД(a, b) = НОД(b, a mod b), где «mod» обозначает операцию нахождения остатка от деления.
Применение НОД включает решение множества задач. Например, для упрощения дробей можно найти НОД числителя и знаменателя и поделить оба числа на него. Это позволит получить наиболее простую дробь.
Также НОД используется при нахождении общих делителей двух или более чисел. Для этого нужно найти НОД для каждой пары чисел и затем сравнить полученные значения. Общие делители могут быть полезны при решении задач по нахождению общих множителей, деления чисел на простые множители и решении других арифметических проблем.
Таким образом, наибольший общий делитель (НОД) является важным понятием в математике, с помощью которого можно решать различные задачи. Метод Евклида позволяет легко находить НОД двух чисел, а его применение включает упрощение дробей, нахождение общих делителей и решение других арифметических задач.
Что такое наибольший общий делитель?
НОД двух чисел можно найти различными способами. Один из самых простых способов – это разложение каждого числа на простые множители и нахождение общих простых множителей. НОД будет равен произведению этих общих множителей.
Есть и другие методы нахождения НОД. Например, алгоритм Евклида. Этот алгоритм основан на том, что НОД двух чисел не меняется, если от большего числа отнять меньшее, пока одно из чисел не станет равным нулю. Затем НОД будет равен последнему ненулевому числу, полученному в результате вычитаний.
НОД имеет много применений в математике и вычислительной технике. Например, задачи нахождения НОД используются при упрощении дробей, поиске общего знаменателя, построении алгоритмов для расчета чисел Фибоначчи и нахождения модулярного обратного числа по модулю.
Общие делители
Для нахождения общих делителей двух чисел необходимо:
- Разложить каждое число на простые множители.
- Найти общие простые множители у этих чисел.
- Умножить все общие простые множители друг на друга.
- Получить НОД, который будет равен произведению общих простых множителей.
Например, для чисел 12 и 18:
- Разложение числа 12 на простые множители: 2 * 2 * 3.
- Разложение числа 18 на простые множители: 2 * 3 * 3.
- Общие простые множители: 2 и 3.
- НОД: 2 * 3 = 6.
Таким образом, общие делители чисел 12 и 18 равны 1, 2, 3 и 6, а их наибольший общий делитель равен 6.
Наибольший общий делитель
Найти НОД можно с помощью нескольких методов:
- Метод деления с остатком. В этом методе два числа делят друг друга с остатком до тех пор, пока не получим нулевой остаток. Наименьшее число, при котором остаток будет равен нулю, и есть НОД.
- Метод простых чисел. В этом методе находим все простые делители для каждого числа и находим их пересечение. Произведение найденных простых делителей будет равно НОД.
- Метод Эвклида. Этот метод заключается в последовательном нахождении остатка от деления предыдущего числа на текущее. Процесс продолжается до тех пор, пока не получим нулевой остаток. Последнее ненулевое число, на котором закончится процесс, и есть НОД.
Нахождение НОД является важной операцией в математике и программировании. Он может использоваться для сокращения дробей, нахождения наименьшего общего кратного и других задач.
Как найти наибольший общий делитель?
Существует несколько методов для нахождения НОД. Один из самых простых способов – это проверка всех возможных делителей двух чисел и выбор наибольшего общего. Например, чтобы найти НОД чисел 12 и 18, нужно проверить делители этих чисел: 1, 2, 3, 6. Наибольший делитель из них – 6, и это и будет НОД чисел 12 и 18.
Еще один метод нахождения НОД – это использование алгоритма Евклида. Суть алгоритма заключается в последовательном вычитании одного числа из другого до тех пор, пока не получится ноль либо два числа равные. Например, чтобы найти НОД чисел 12 и 18, мы последовательно будем вычитать меньшее число из большего: 18 — 12 = 6, 12 — 6 = 6. Таким образом, НОД чисел 12 и 18 также равен 6.
Кроме методов перебора и алгоритма Евклида, существуют и другие алгоритмы, такие как факторизация чисел и расширенный алгоритм Евклида. Эти методы могут быть эффективны в зависимости от входных данных и контекста задачи.
Найденный НОД может быть использован для решения различных задач, таких как сокращение дробей, проверка на взаимную простоту и другие математические операции.
Таким образом, нахождение наибольшего общего делителя является важной задачей в математике и может быть выполнено с помощью различных методов.
Метод Евклида
Основная идея метода Евклида заключается в том, что все последующие итерации состоят из вычисления остатка от деления двух чисел и замены большего числа на этот остаток. Процесс продолжается до тех пор, пока остаток не станет равен 0. Когда это происходит, последнее ненулевое число — и есть НОД.
Пример:
Для нахождения НОД чисел 48 и 18, мы сначала делим 48 на 18 и получаем остаток 12. Затем делим 18 на 12 и получаем остаток 6. И, наконец, делим 12 на 6 и получаем остаток 0. Поскольку остаток стал равен 0, НОД чисел 48 и 18 равен 6.
Метод Евклида можно применять не только для двух чисел, но и для большего количества чисел. Для этого нужно последовательно находить НОД для каждой пары чисел, заменяя большее число остатком от деления.
Разложение на простые множители
Чтобы разложить число на простые множители, сначала мы проверяем, делится ли оно на 2. Если да, то мы делим его на 2 и продолжаем делить на 2 до тех пор, пока не получим нечетное число.
Затем мы продолжаем проверку на делимость для всех нечетных чисел, начиная с 3 и идя по порядку. Если число делится на какое-то нечетное число, мы делим его на это число и продолжаем делить, пока числитель не станет равным 1.
Результатом разложения на простые множители является произведение всех полученных простых чисел. Например, число 48 может быть разложено на простые множители как 2 * 2 * 2 * 2 * 3.
Разложение на простые множители позволяет нам лучше понять структуру числа и использовать его свойства при решении различных задач. Также разложение на простые множители может быть полезно при нахождении наибольшего общего делителя и наименьшего общего кратного двух или более чисел.
Вопрос-ответ:
Что такое наибольший общий делитель?
Наибольший общий делитель (НОД) двух или более чисел — это наибольшее число, которое делится без остатка на все эти числа. Например, для чисел 12 и 18, НОД равен 6, так как 6 делится без остатка на оба числа.
Зачем нужен наибольший общий делитель?
НОД необходим для решения множества математических задач. Он используется при сокращении дробей, нахождении общего знаменателя, определении несократимых дробей, решении диофантовых уравнений и других задачах.
Как найти наибольший общий делитель?
Существует несколько методов для нахождения НОД. Один из самых простых и распространенных методов — это метод Эвклида. Он основан на следующем принципе: для двух чисел A и B, если A больше B, то НОД(A, B) равен НОД(B, A % B), где % обозначает операцию остатка от деления. Этот процесс повторяется, пока B не станет равным 0, в этот момент A станет НОД.
Как найти наибольший общий делитель через разложение на простые множители?
Другой способ нахождения НОД — это разложение чисел на простые множители и последующее нахождение общих простых множителей. Для двух чисел, например, 24 и 36, разложение на простые множители будет равно 2 * 2 * 2 * 3 и 2 * 2 * 3 * 3 соответственно. Общие простые множители — это 2 * 2 * 3, что равно 12, то есть НОД(24, 36) = 12.
Как применить наибольший общий делитель в решении задачи?
Применение НОД в решении задач зависит от самой задачи. Например, если задача требует нахождения наименьшего общего кратного чисел, можно использовать НОД. НОК двух чисел — это их произведение, поделенное на их НОД. Также НОД может использоваться для определения несократимых дробей или решения диофантовых уравнений.