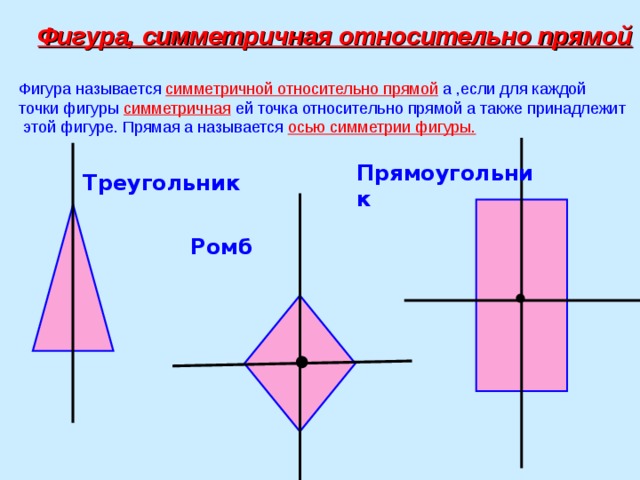
Симметрия является одним из основных понятий в геометрии. Понимание и применение симметрии позволяют лучше понять и проанализировать различные фигуры и объекты в пространстве. Одним из видов симметрии является осевая симметрия, которая определяется относительно данной прямой.
Осевая симметрия предполагает, что каждая точка фигуры имеет точно одну пару, лежащую на прямой отражения. При этом расстояние от исходной точки до прямой отражения и отраженной точки до этой же прямой равны. Другими словами, фигура симметрична сама относительно себя относительно данной прямой.
Примером фигуры, которая является симметричной относительно данной прямой, может быть отрезок. Если отрезок является частью прямой, то он является симметричным относительно этой прямой. Каждая точка на отрезке имеет пару, лежащую на этой же прямой и симметричную относительно нее. То есть, если мы возьмем отрезок и его отразим относительно данной прямой, то получим исходный отрезок.
Определение симметричной фигуры относительно прямой
Другими словами, если взять любую точку фигуры и провести через нее прямую, являющуюся осью симметрии, то эту точку можно отобразить на другую сторону этой прямой таким образом, чтобы расстояния между отраженной точкой и прямой были равны расстояниям между исходной точкой и прямой.
Примеры симметричных фигур относительно прямой:
— Квадрат является симметричной фигурой относительно горизонтальной и вертикальной осей симметрии.
— Круг является симметричной фигурой относительно любой прямой, проходящей через его центр.
Что такое симметричная фигура?

В случае симметричной фигуры, каждая точка на одной стороне от оси симметрии имеет соответствующую точку на другой стороне, которая находится на той же самой удаленности от оси, но противоположна ей.
Симметричные фигуры могут иметь разную форму и размеры. Они могут быть симметричными как относительно горизонтальной оси, так и относительно вертикальной оси, а также относительно наклонной оси.
Ось симметрии может быть явной и видимой, как это, например, в случае симметричных относительно вертикальной и горизонтальной оси фигур, таких как квадрат или равнобедренный треугольник. Однако, в некоторых случаях, ось симметрии может быть воображаемой или скрытой, как это, например, в случае произвольного многоугольника.
| Симметричная фигура Пример
| Несимметричная фигура Пример
|
Тип симметрии может быть важным свойством фигуры. Симметричные фигуры имеют характерные свойства и могут выполняться ряд правил, которые позволяют облегчить их изучение и анализ.
Симметрия играет важную роль в различных областях, включая математику, физику, биологию, искусство и дизайн. Понимание симметрии фигур позволяет увидеть гармонию и баланс, а также использовать ее в создании красивых и эстетически приятных объектов и композиций.
Примеры симметричных фигур
Пример 1: Прямоугольник
Прямоугольник имеет две симметрийные оси – горизонтальную и вертикальную. Если прямоугольник сложить по соответствующим симметричным линиям, то получится совпадение фигуры с самой собой.
Пример 2: Круг
Круг является симметричной фигурой, так как любую его точку можно совместить с противоположной точкой относительно центра круга. Это называется осевой симметрией.
Пример 3: Равносторонний треугольник
Равносторонний треугольник – это треугольник у которого все стороны равны. Он обладает тремя симметричными осями – каждая сторона равностороннего треугольника является осью симметрии.
Это лишь несколько примеров симметричных фигур. Вокруг нас много других фигур, которые также являются симметричными. Изучение симметричных фигур помогает понять принципы симметрии и развивает визуальное мышление.
Симметрия относительно горизонтальной прямой
Если фигура симметрична относительно горизонтальной прямой, то она остается неизменной при отражении вокруг этой прямой. То есть, точки, лежащие на прямой, остаются на месте, а все остальные точки фигуры переходят на равное расстояние от прямой, но в противоположном направлении.
Примерами фигур, которые обладают симметрией относительно горизонтальной прямой, являются такие геометрические фигуры, как прямоугольник, квадрат, треугольник и др.
Симметрия относительно горизонтальной прямой имеет много применений в геометрии, искусстве и дизайне. Она позволяет создавать сбалансированные и гармоничные композиции, где симметричные элементы создают впечатление упорядоченности и спокойствия.
Симметрия относительно вертикальной прямой
Симметрия относительно вертикальной прямой является особым случаем симметрии относительно оси симметрии. В этом случае вертикальная прямая выступает в роли оси симметрии, которая делит фигуру на две симметричные половины.
Симметрия относительно вертикальной прямой имеет множество применений в различных областях. Например, в геометрии она позволяет определить свойства и связи между фигурами. В проективной геометрии симметрия относительно вертикальной прямой играет важную роль при решении задач по построению и изучению прямых и плоскостей.
Симметрия относительно вертикальной прямой имеет также широкое применение в живой природе и в искусстве. Многие симметричные формы и узоры, которые встречаются в природе и в художественных произведениях, основаны на симметрии относительно вертикальной прямой.
Таким образом, симметрия относительно вертикальной прямой является важным понятием в геометрии и имеет широкое применение в различных областях. Понимание и использование этой симметрии позволяет анализировать и создавать фигуры, узоры и структуры, которые обладают особыми свойствами и эстетическими характеристиками.
Симметрия относительно наклонной прямой
Когда говорят о симметрии относительно наклонной прямой, обычно имеют в виду отражение фигуры относительно этой прямой. Например, отражение треугольника, прямоугольника или любой другой фигуры относительно наклонной прямой дает новую фигуру, которая симметрична относительно этой прямой.
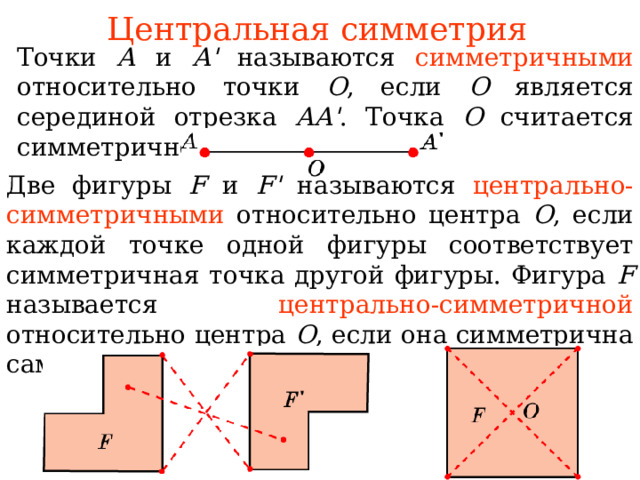
Симметрия относительно наклонной прямой является одной из видов симметрии в геометрии. Другие виды симметрии включают симметрию относительно горизонтальной прямой, вертикальной прямой и центральной точки.
Симметрия относительно наклонной прямой широко используется в геометрии и графике, а также в архитектуре и дизайне. Она помогает создавать гармоничные и сбалансированные композиции, а также обладает эстетической привлекательностью.
Как определить симметричную фигуру относительно данной прямой?
Чтобы определить, является ли фигура симметричной относительно данной прямой, можно выполнить следующие шаги:
- Нарисуйте данную прямую и положите фигуру на один из ее концов или в центр.
- Поставьте зеркало так, чтобы оно перпендикулярно поверхности источника света (прямой).
- Отразите фигуру относительно зеркала.
- Сравните отраженную фигуру с исходной фигурой.
- Если каждая точка исходной фигуры соответствует точке отраженной фигуры, то фигура является симметричной относительно данной прямой.
Если фигура не является симметричной относительно прямой, то она может быть симметричной относительно другой прямой или вообще не иметь симметрии.
Симметрия имеет широкое применение в разных областях, таких как дизайн, архитектура и искусство. Понимание, как определить симметричную фигуру относительно данной прямой, поможет при анализе и создании различных геометрических форм и улучшит визуальное восприятие.
Вопрос-ответ:
Какая фигура называется симметричной относительно данной прямой?
Фигура, которая симметрична относительно данной прямой, называется отражением этой фигуры.
Как определить, является ли фигура симметричной относительно данной прямой?
Чтобы определить, является ли фигура симметричной относительно данной прямой, нужно провести прямую, которая является осью симметрии, и посмотреть, будут ли соответствующие участки фигуры симметричными относительно этой оси.
Можете привести пример фигуры, которая является симметричной относительно горизонтальной прямой?
Примером фигуры, которая является симметричной относительно горизонтальной прямой, может быть прямоугольник, если ось симметрии находится на его горизонтальной средней линии. В этом случае верхняя половина прямоугольника будет симметричной относительно нижней половины.
Можно ли сказать, что у фигуры может быть несколько осей симметрии?
Да, у фигуры может быть несколько осей симметрии. Например, у круга бесконечное количество осей симметрии, так как любая прямая, проходящая через его центр, будет осью симметрии.
Что происходит с фигурой, когда она является симметричной относительно данной прямой?
Когда фигура является симметричной относительно данной прямой, каждая точка фигуры имеет свою симметричную точку относительно этой прямой. Это значит, что если подвинуть каждую точку фигуры на такое же расстояние от прямой, но в противоположном направлении, то получится исходная фигура.
Как называется фигура, которая симметрична относительно горизонтальной прямой?
Фигура, которая симметрична относительно горизонтальной прямой, называется отражением. Это означает, что каждая точка на одной стороне прямой отражается в точку на другой стороне прямой так, что расстояние от прямой до исходной точки равно расстоянию от прямой до отраженной точки.

