Понятие параллельных прямых широко используется в геометрии и математике. При изучении параллельных прямых часто возникает вопрос о том, как называются точки, которые лежат на обеих параллельных прямых относительно третьей прямой. В данной статье мы рассмотрим этот вопрос подробно и попытаемся найти ответ на него.
Представим себе две параллельные прямые, расположенные на плоскости. Теперь допустим, что мы проводим третью прямую, которая пересекает одну из параллельных прямых. Точки, которые лежат на обеих параллельных прямых относительно этой третьей прямой, имеют свое название.
Такие точки называются соответственными точками. Иными словами, каждая точка одной из параллельных прямых имеет соответствующую точку на другой параллельной прямой. Это свойство параллельных прямых является важным при решении геометрических задач и анализе пространственных отношений.
Параллельные прямые
Чтобы показать, что две прямые параллельные, используется символ «||». Например, AB || CD означает, что прямая AB параллельна прямой CD. Здесь А и В — точки на первой прямой, а С и D — точки на второй прямой.
Существует несколько способов определить, что две прямые параллельные. Один из самых простых способов — проверить их угловой коэффициент. Если у двух прямых угловой коэффициенты равны, то они параллельны.
Свойства параллельных прямых:
1. Расстояние между прямыми всегда одинаково. Это означает, что если провести отрезок, перпендикулярный обеим прямым, то его длина будет постоянной и равной расстоянию между прямыми.
2. Углы, образованные пересекающей прямой и прямыми, параллельными друг другу, равны.
3. При параллельном пересечении прямые создают параллельные отрезки. Например, если две параллельные прямые пересекают третью прямую, то отрезки, образованные этим пересечением на каждой прямой, также будут параллельными.
Таблица:
| Свойство | Описание |
|---|---|
| Расстояние между прямыми | Расстояние между двумя параллельными прямыми всегда одинаково. |
| Углы, образованные пересекающей прямой и параллельными прямыми | Углы, образованные при пересечении прямой с параллельными ей прямыми, равны. |
| Параллельные отрезки | При параллельном пересечении прямые создают параллельные отрезки. |
Определение параллельных прямых
Существует несколько способов определить параллельные прямые. Один из них — это использование аксиомы Евклида, согласно которой, если две прямые на плоскости пересекаются с третьей прямой таким образом, что сумма внутренних углов на одной стороне меньше 180 градусов, то эти две прямые параллельны.
Другим способом определения параллельных прямых является использование параллельных прямых теоремы, которая гласит, что если две прямые пересекаются с третьей прямой под углом, то их внутренние углы на одной стороне равны. И наоборот, если внутренние углы на одной стороне прямых равны, то эти прямые параллельны.
Свойства параллельных прямых:
| 1. | Параллельные прямые имеют одинаковый наклон или угол наклона. |
| 2. | Параллельные прямые расстояние между ними постоянно и не меняется. |
| 3. | Параллельные прямые не пересекаются ни в одной точке. |
Свойства параллельных прямых
Свойство 1: Углы, образованные параллельными прямыми и пересекающей их прямой, равны.

Если две прямые параллельны и пересекаются третьей прямой, то углы, образованные этими прямыми с третьей прямой, будут равными. Например, угол A и угол B на рисунке ниже будут равными.
|
|
|
Свойство 2: Углы, образованные параллельными прямыми и пересекающимися прямыми, равны попарно.
Если две прямые параллельны и пересекаются другими прямыми, то закономерно, что углы, образованные параллельными прямыми с пересекающимися прямыми, будут равными попарно. На рисунке ниже углы A и D равны, углы B и E равны, а углы C и F равны.
|
|
|
Эти свойства параллельных прямых очень полезны при решении различных задач в геометрии. Они позволяют находить неизвестные углы и устанавливать равенства между углами, что упрощает расчеты и доказательства.
Прямая, пересекающая параллельные прямые
Прямые, которые находятся в одной плоскости и не пересекаются, называются параллельными прямыми. Если через параллельные прямые провести другую прямую, которая пересекает обе параллельные прямые, то эта прямая называется пересекающей параллельные.
Пересекающая параллельные прямые образует особый угол с каждой из параллельных прямых. Один из особых углов называется внутренним углом, а другой – внешним. Внутренний угол лежит внутри параллельных прямых, а внешний угол – снаружи параллельных прямых.
Из свойств пересекающих параллельные прямые можно вывести интересные следствия. Например, если в некотором треугольнике одна сторона параллельна одной из сторон исходного треугольника и пересекает две другие стороны, то соответствующие углы этого треугольника будут равны соответствующим углам исходного треугольника.
Свойства пересекающих параллельные прямые:
- Внутренние углы, образованные пересекающими параллельными прямыми, равны между собой;
- Внешние углы, образованные пересекающими параллельными прямыми, равны при пересечении прямыми одного и того же угла;
- Сумма внутренних углов в каждой паре пересекающих прямых равна 180°;
- Внутренний угол, образованный пересекающей прямой и одной из параллельных прямых, равен внешнему углу, образованному другой параллельной прямой и продолжением пересекающей прямой.
Определение пересекающей прямой
Критерии для определения пересекающей прямой:
- Угол между пересекающей прямой и параллельными прямыми не равен 0 градусам.
- Пересекающая прямая имеет общую точку с каждой из параллельных прямых.
Чтобы понять, находятся ли две прямые в параллельном положении, можно использовать теорему о параллельных прямых:
| Если две прямые пересекаются третьей прямой так, что внутренние и внешние углы находятся взаимно дополняющими положениями, то эти две прямые являются параллельными. |
Если данные критерии соблюдаются, то прямая может быть определена как пересекающая, иначе она будет параллельна другим прямым.
Свойства пересекающей прямой
- Пересекающая прямая образует с параллельными прямыми систему углов, которые называются вертикальными углами.
- Угол между пересекающей прямой и одной из параллельных прямых равен углу между пересекающей прямой и другой параллельной прямой.
- Пересекающая прямая делит параллельные прямые на сегменты, которые образуют однонаправленные углы с пересекающей прямой.
- Если пересекающая прямая является биссектрисой углов между параллельными прямыми, то эти углы являются равными.
Свойства пересекающей прямой могут быть полезны при решении различных задач геометрии или при анализе поведения системы параллельных прямых.
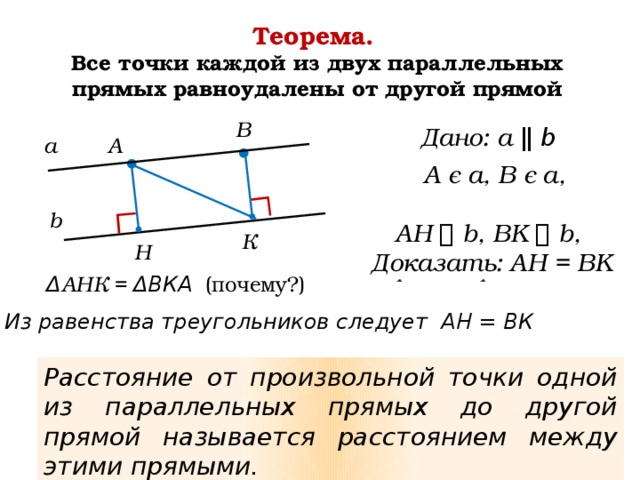
Все точки каждой из параллельных прямых относительно другой прямой
Эти точки называются соответственными точками, потому что они имеют одинаковое расстояние до третьей прямой. Другими словами, каждая точка одной прямой соответствует определенной точке другой прямой и наоборот.
Соответственные точки образуют плоскость, которая параллельна третьей прямой и называется плоскостью соответствия. Эта плоскость содержит бесконечное множество точек, поскольку для каждой точки третьей прямой существует точка на каждой из параллельных прямых, которая соответствует ей.
В геометрии параллельные прямые и их соответственные точки являются важными объектами изучения, так как они позволяют строить разнообразные фигуры и решать задачи на планировании и конструировании.
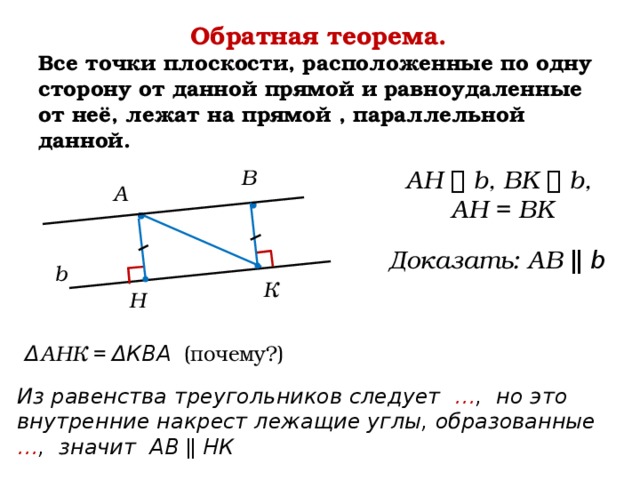
Свойства точек относительно другой прямой
При рассмотрении двух параллельных прямых, важно изучить свойства точек в отношении третьей прямой. Рассмотрим основные свойства:
| Тип точки | Описание |
|---|---|
| Соответствующие точки | Точки, находящиеся на пересекаемых прямых, лежащие по одну сторону от параллельных прямых и имеющие одинаковое расстояние до них. |
| Составные точки | Точки, находящиеся на пересекаемых прямых, лежащие по одну сторону от параллельных прямых и имеющие различное расстояние до них. |
| Конфлюэнтные точки | Точки, находящиеся на пересекаемых прямых, лежащие по одну сторону от параллельных прямых и имеющие одинаковое расстояние до них. |
Знание свойств точек относительно другой прямой позволяет анализировать и решать геометрические задачи, связанные с параллельными прямыми и их пересечениями с третьей прямой.
Вопрос-ответ:
Как называется множество всех точек, которые находятся на одинаковом расстоянии от двух параллельных прямых?
Такое множество называется плоскость.
Можно ли найти точку, которая находится на одинаковом расстоянии от двух параллельных прямых?
Да, можно. Эта точка находится на пересечении перпендикуляров, опущенных из любой точки одной из этих прямых на другую.
Как называется линия, проходящая через точку, которая находится на одинаковом расстоянии от двух параллельных прямых?
Эта линия называется нормаль или перпендикуляр к параллельным прямым.
Что представляет собой множество всех точек, которые находятся на одинаковом расстоянии от двух параллельных прямых?
Это множество представляет собой плоскость, которая перпендикулярна к параллельным прямым.
Если две параллельные прямые имеют одну и ту же наклонную линию, как называется эта линия?
Если две параллельные прямые имеют одну и ту же наклонную линию, эта линия называется прямая-пересекающая.

