
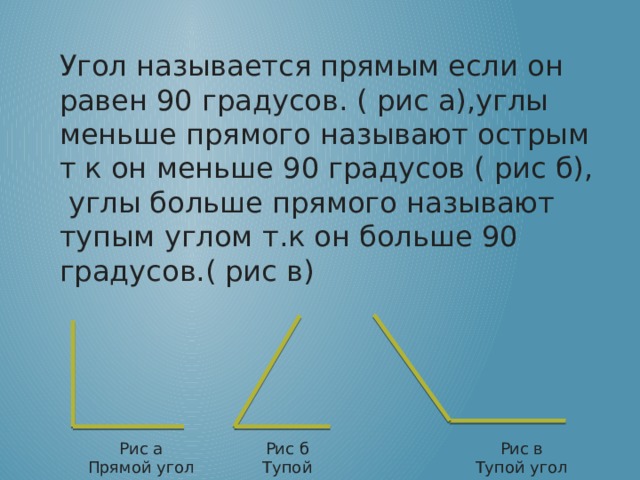
Угол – это геометрическая фигура, которая образуется двумя лучами, исходящими из одной точки, называемой вершиной. В зависимости от величины угла, он может быть острый, прямой, тупой или полный. В данной статье рассмотрим углы, которые меньше 90 градусов.
Угол меньше 90 градусов называется острым углом. Острый угол превышает ноль градусов и меньше 90 градусов. Это значит, что оба луча, образующих угол, отклоняются друг от друга, но не достигают прямого угла (90 градусов).
Острые углы встречаются в различных областях жизни. Например, в геометрии острые углы используются для расчета площадей и объемов различных фигур. В архитектуре острые углы считаются символом динамики и энергии, они используются для создания необычных форм и композиций зданий. В фотографии острые углы помогают создавать интересные ракурсы и выделить особенности объекта съемки.
Определение острого угла
Острый угол обладает следующими характеристиками:
- Меряется в градусах, минутах и секундах или в радианах.
- Угол между двумя положительными осами координат в двумерном пространстве.
- Измеряется от оси X до луча, исходящего из начала координат.
- Положение угла может быть определено с использованием трех координат: X, Y и Z.
Острый угол является одним из основных понятий в геометрии, используемых в решении различных задач и задач практического применения.
Угол меньше 90 градусов — что это такое?
Угол меньше 90 градусов называется остроугольным углом. Он представляет собой угол, который меньше прямого угла, то есть угла в размере 90 градусов.
Остроугольный угол можно представить себе как угол, который имеет острый вершийс и две стороны, помещающиеся в прямоугольник. Остроугольный угол может быть измерен в градусах или радианах, и величина угла определяется между прямыми линиями, исходящими из его вершины.
Остроугольные углы встречаются во многих областях, таких как геометрия, физика, инженерия и астрономия. Они используются для измерения углов, определения расстояний и направлений, а также для решения различных задач и проблем.
Остроугольные углы имеют свои характеристики и свойства. Они могут быть равны между собой или между собой и другими углами. Остроугольные треугольники, которые имеют три остроугольных угла, обладают определенными закономерностями и свойствами, которые используются при их изучении и решении задач.
Остроугольные углы имеют важное значение в нашей жизни и в науке. Они помогают нам понять и объяснить многие явления и процессы, которые происходят в природе и в нашей окружающей среде.
Что значит острый угол?
Острый угол имеет свои особенности и свойства. Он всегда меньше прямого и тупого угла, а его величина может быть разной, от самого маленького до почти 90 градусов.
Острый угол можно измерить с помощью градусного измерителя или другого инструмента, способного определить величину угла. Также существуют специальные таблицы и таблицы логарифмов, которые позволяют определить значение угла с помощью известных величин.
Острый углы часто встречаются в геометрии и физике. Они используются для расчета и изучения различных явлений и объектов, таких как тригонометрические функции, треугольники, векторы и другие. Также они играют важную роль в пространстве и времени, поскольку определяют углы между объектами, движениями и силами.
| Тип угла | Описание |
|---|---|
| Прямой угол | Угол, равный 90 градусам |
| Тупой угол | Угол, больший 90 градусов и меньший 180 градусов |
| Разносторонний угол | Угол, у которого все стороны, лежащие на плоскостях, прямолинейные |
Острый угол имеет множество приложений и применений. Он используется в геодезии, строительстве, компьютерной графике, архитектуре, физике, аэронавтике и многих других областях. Знание и понимание острого угла позволяет решать сложные задачи и создавать новые технологии и методы исследования.
Примеры острых углов
1. Углы в геометрии
В геометрии острые углы широко используются при изучении геометрических фигур. Например, в треугольниках два угла всегда являются острыми, а третий угол может быть прямым, тупым или острым в зависимости от сторон и углов треугольника.
2. Острый угол в архитектуре
Архитектурные сооружения могут содержать острые углы. Например, в зубцах готического стиля часто использовались острые углы, что придавало зданиям уникальность и эффектность. Также острые углы можно увидеть в острых арках и оконных проемах.
3. Острые углы в природе
В природе можно встретить множество примеров острых углов. Разветвленные ветви деревьев, остроугольные камни и скалы, острые формы листьев – все это примеры острых углов, которые можно наблюдать в окружающей нас природе.
Острые углы являются важной частью нашей жизни и повседневной деятельности. Важно уметь распознавать и понимать их значения и применение в разных сферах.
Как найти меру острого угла?
Для нахождения меры острого угла можно использовать несколько методов:
1. Использование известных углов:
Если вам даны значения нескольких углов в треугольнике или другой фигуре, вы можете найти меру острого угла, используя свойства треугольников и суммы углов. Например, если у вас есть треугольник, в котором известны значения двух углов (например, 30 градусов и 60 градусов), то мера острого угла равна 90 градусов минус сумма известных углов (в данном случае 30+60=90 градусов, поэтому острый угол будет равен 0 градусов).
2. Использование тригонометрических функций:
Если у вас даны значения длин сторон треугольника, вы можете использовать тригонометрические функции (синус, косинус, тангенс) для нахождения меры острого угла. В этом случае вам понадобится таблица значений функций или калькулятор, поддерживающий тригонометрические функции. Например, если вам даны длины двух сторон треугольника (например, 3 и 4) и вы хотите найти меру острого угла, противолежащую стороне длиной 3, вы можете использовать функцию арктангенс (tan-1) и написать выражение sin-1(3/4) => около 36.87 градусов.
Важно помнить, что нахождение меры острого угла требует знания свойств угловых функций, треугольников и других геометрических фигур. При использовании математических методов всегда проверяйте свои расчеты и внимательно читайте задачу.
Острый угол в геометрии
В геометрии острые углы играют важную роль и используются в решении различных задач. Например, острые углы часто встречаются в треугольниках. Если треугольник является острым, то все его углы будут острыми.
Острый угол можно измерить с помощью градусов, минут и секунд. Измерение угла происходит с помощью угломера или градусного круга. Угол измеряется относительно оси угломера или центра градусного круга.
Острый угол может быть равным или меньше других углов, таких как прямой угол (90 градусов) или тупой угол (больше 90 градусов). Острый угол будет больше, чем острые углы в прямоугольном треугольнике, но меньше тупых углов в этом же треугольнике.
Острый угол важен для понимания геометрических принципов и концепций. Его изучение помогает решать задачи, связанные с фигурами и пространством. Понимание острого угла также полезно при изучении других тем, таких как тригонометрия и геометрические преобразования.
Значение острого угла в разных науках
Математика
В математике острый угол имеет особое значение при изучении геометрии. Острые углы используются для определения разных фигур, таких как треугольники или многоугольники. Они также используются для решения различных задач и формулирования геометрических теорем.
Физика, астрономия и геодезия
В физике, астрономии и геодезии острые углы используются для измерения расстояний. С помощью острых углов можно определить угол наклона плоскости или поверхности, а также провести геодезические измерения или расчеты параболических траекторий движения небесных тел.
В общем, значение острого угла в разных науках относится к изучению форм и расстояний, а также к различным вычислениям и определениям, которые помогают в области геометрии, физики и астрономии.
Важность понимания острых углов
Геометрическое определение острых углов
Острый угол определяется двумя лучами, начало одного из которых соединено с концом другого луча, и они вместе образуют конечную точку, расположенную внутри круга с центром на оси образования угла.
Острый угол характеризуется следующим свойствами:
- Меньше 90 градусов;
- Лежит между двумя полными углами;
- Может быть частью треугольника или любой другой фигуры;
- Всегда имеет острый вершинный угол.
Применение понимания острых углов
Понимание острых углов имеет множество практических применений в нашей повседневной жизни. Рассмотрим некоторые из них:
- Архитектура: Остроугольные треугольники используются для определения высоты зданий и конструкций. Инженеры и архитекторы должны правильно и точно определить острые углы, чтобы обеспечить правильные пропорции и стабильность строительных сооружений.
- Картография: Остроугольные углы используются для измерения направлений на картах и навигации. Они помогают в определении точных координат и маршрутов.
- Наука: В физике и других научных областях острые углы используются для измерения и анализа различных параметров и явлений.
- Игры: Остроугольные углы могут использоваться в головоломках и логических играх, помогая развивать абстрактное мышление и логическое рассуждение.
Вопрос-ответ:
Что такое угол меньше 90 градусов?
Угол меньше 90 градусов называется остроугольным углом.
Как называется угол, который меньше прямого угла?
Угол, который меньше прямого угла (90 градусов), называется остроугольным.
Какой термин применяется для угла, меньшего 90 градусов?
Угол, который меньше 90 градусов, называется остроугольным углом.
Каким названием обладает угол, чья мера меньше 90 градусов?
Угол, чья мера меньше 90 градусов, имеет название — остроугольный угол.