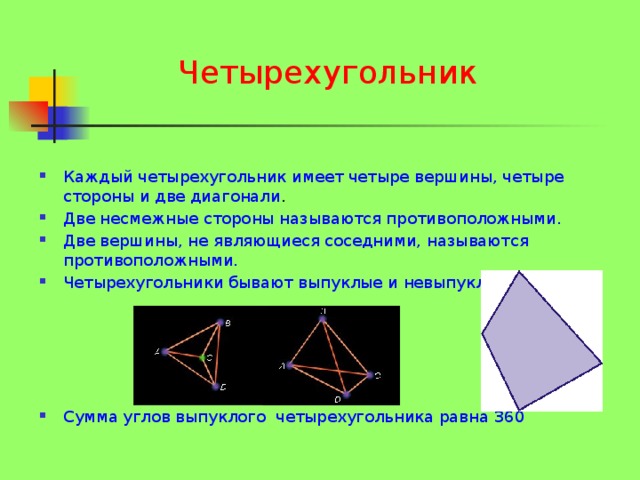
В математике четырехугольник — это фигура, состоящая из четырех отрезков, называемых сторонами. Каждая сторона соединяет две соседние вершины четырехугольника. Однако некоторые четырехугольники имеют особые стороны — не смежные, не соединяющие две вершины в соседних парах.
Эти особые стороны называются диагоналями. Каждая диагональ соединяет две несмежные вершины четырехугольника. Именно диагонали позволяют получить дополнительные свойства и характеристики четырехугольника, такие как: периметр, площадь, длины сторон и т.д.
Отличительной особенностью диагоналей является то, что они пересекаются внутри четырехугольника. В некоторых случаях пересечение диагоналей образует точку, называемую центром четырехугольника. Диагонали могут служить базисом для вычисления различных характеристик, помогая нам лучше понять структуру и свойства четырехугольника.
Определение четырехугольника
Две не смежные стороны четырехугольника — это такие стороны, которые не имеют общей вершины. Они могут быть расположены противоположно друг другу или находиться по соседству с другими сторонами.
Четырехугольники могут быть различных типов, включая прямоугольники, квадраты, ромбы, параллелограммы, трапеции и другие. Каждый тип четырехугольника имеет свои особенности и свойства, которые могут быть использованы для их классификации и изучения.
Знание о двух не смежных сторонах четырехугольника помогает определить его форму и характеристики, такие как типы углов и соотношения сторон. Это важно для решения геометрических задач связанных с четырехугольниками и их применения в различных областях, таких как архитектура, инженерия и графика.
Структура четырехугольника
Стороны четырехугольника
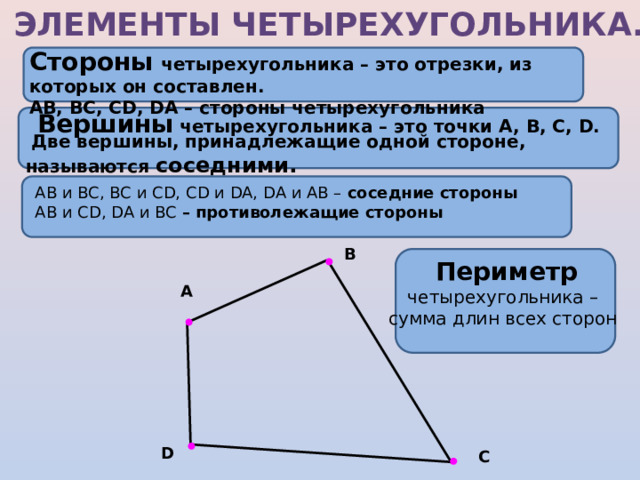
В четырехугольнике есть четыре стороны, которые соединяют вершины фигуры. Длины сторон могут быть разными, что дает четырехугольнику различные формы. Для обозначения сторон часто используют буквы a, b, c и d.
Углы четырехугольника
У четырехугольника также есть четыре угла. Углы могут быть острыми, тупыми или прямыми в зависимости от их величины. Для обозначения углов часто используют греческие буквы α, β, γ и δ. Углы между смежными сторонами называются внутренними углами, а углы между продолжениями несмежных сторон — внешними углами.
Свойства четырехугольника
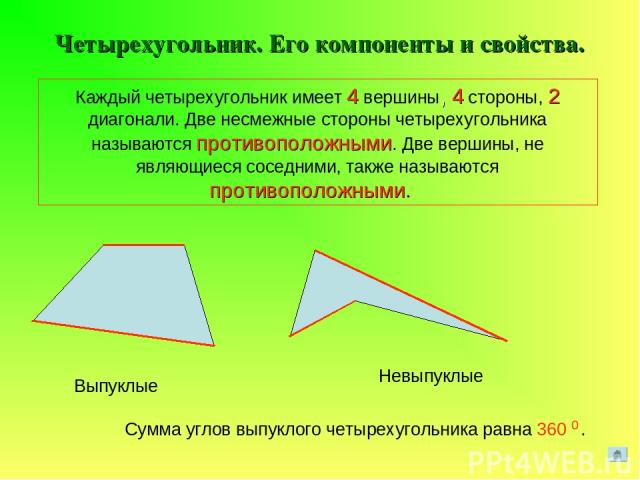
- Сумма всех углов четырехугольника равна 360 градусов.
- Две смежные стороны могут быть смежными сторонами с двумя различными углами.
- Две несмежные стороны не могут быть смежными сторонами.
- Сумма длин двух сторон четырехугольника всегда больше, чем длины любых двух его остальных сторон.
Стороны четырехугольника
Каждая сторона четырехугольника имеет длину, которая выражается в единицах измерения. Для удобства обозначения стороны обычно используют маленькие буквы латинского алфавита: а, b, c и d. Значения сторон могут быть различными, и каждая сторона может быть разной длины.
Стороны четырехугольника могут быть параллельными или пересекаться. Если все стороны четырехугольника параллельны попарно, то он называется параллелограммом. Если две стороны параллелограмма имеют одинаковую длину, то он называется ромбом. Если все стороны ромба имеют одинаковую длину, то он называется квадратом.
Стороны четырехугольника также могут образовывать углы. Вершины, в которых пересекаются две соседние стороны, называются углами четырехугольника. Углы могут быть острыми, прямыми или тупыми.
Зная значения сторон, можно вычислить периметр четырехугольника, который равен сумме длин всех его сторон. Периметр позволяет определить длину контура фигуры и оценить длину пути вдоль этого контура.
Углы четырехугольника
Углы четырехугольника это внутренние углы, образованные пересечением двух сторон. В четырехугольнике есть четыре угла: два противоположных угла находятся на одной паре противоположных сторон, и два смежных угла находятся на другой паре противоположных сторон.
Два противоположных угла называются смежными, если они находятся на разных сторонах четырехугольника. Например, если мы рассмотрим четырехугольник ABCD, то углы A и C будут смежными углами, и углы B и D будут также смежными углами.
Два смежных угла называются противоположными, если они находятся на одной противоположной стороне четырехугольника. Например, если мы рассмотрим четырехугольник ABCD, то углы A и B будут противоположными углами, и углы C и D будут также противоположными углами.
Типы четырехугольников
В геометрии существует несколько типов четырехугольников, которые различаются по свойствам и структуре.
1. Прямоугольник
Прямоугольник — это четырехугольник, у которого все углы прямые. В прямоугольнике противоположные стороны параллельны и равны по длине.
2. Ромб
Ромб — это четырехугольник, у которого все стороны равны по длине. Ромб также имеет свойство равенства диагоналей: диагонали ромба пересекаются под прямым углом и делятся пополам.
В том случае, если две несмежные стороны четырехугольника равны по длине, но прямых углов у него нет, такой четырехугольник называется квадратом.
Свойства четырехугольников
1. Сумма углов
Сумма углов внутри любого четырехугольника всегда равна 360 градусов. Это означает, что если измерить каждый угол и сложить их значения, получится 360 градусов.
2. Диагонали
Четырехугольник имеет две диагонали – отрезки, соединяющие несмежные вершины. У четырехугольников с определенными свойствами диагонали обладают некоторыми особенностями. Например, в ромбе диагонали являются взаимно перпендикулярными и делятся пополам. В прямоугольнике и квадрате диагонали также взаимно перпендикулярны, но не обязательно делятся пополам.
Осознание этих свойств позволяет легче работать с четырехугольниками и применять их в различных задачах в геометрии и физике. Знание свойств четырехугольников также полезно при проведении математических доказательств и дедукций.
| Название четырехугольника | Свойства диагоналей |
|---|---|
| Ромб | Взаимно перпендикулярны, делятся пополам |
| Прямоугольник | Взаимно перпендикулярны |
| Квадрат | Взаимно перпендикулярны |
Высота четырехугольника
Высота обладает следующими свойствами:
- Высота является кратчайшим расстоянием между вершиной и прямой, на которой лежит противоположная сторона.
- Высота делит четырехугольник на два треугольника.
- Величина высоты зависит от длин сторон и углов четырехугольника.
Для нахождения высоты четырехугольника можно использовать различные методы, в зависимости от доступных данных. Например, если известны координаты вершин четырехугольника, можно воспользоваться формулами для определения уравнения прямой, на которой лежит противоположная сторона, и перпендикулярной к ней. Затем можно найти точку пересечения этих прямых и вычислить длину отрезка между вершиной и этой точкой.
Зная длины сторон четырехугольника, можно применить формулу для вычисления площади, а затем воспользоваться формулой для вычисления высоты через площадь и длину противоположной стороны.
Высота четырехугольника играет важную роль в геометрии, используется при решении задач и находит применение в различных областях науки и техники.
Площадь четырехугольника
Вычисление площади четырехугольника
Для прямоугольника или квадрата площадь вычисляется по формуле: S = a * b, где a и b — длины его сторон.
Если известны длины всех четырех сторон четырехугольника и один из его углов, можно воспользоваться формулой Герона для вычисления площади.
Таблица с формулами для вычисления площади
| Форма четырехугольника | Формула для вычисления площади |
|---|---|
| Прямоугольник | S = a * b |
| Квадрат | S = a * a |
| Трапеция | S = (a + b) * h / 2 |
В случае, если четырехугольник имеет не смежные стороны, необходимо знать дополнительные параметры или использовать сложные формулы для вычисления площади. В таких случаях обращайтесь к специализированной литературе или консультируйтесь с профессионалами в области геометрии.
Вопрос-ответ:
Что такое несмежные стороны четырехугольника?
Несмежные стороны четырехугольника — это две стороны, которые не имеют общей вершины.
Какие могут быть несмежные стороны в четырехугольнике?
В четырехугольнике могут быть различные комбинации несмежных сторон, например, AB и CD, AC и BD, или AD и BC.
Зачем нужно называть несмежные стороны четырехугольника?
Называть несмежные стороны четырехугольника нужно для удобства описания и классификации фигуры. Это помогает нам более точно определить форму и свойства четырехугольника.
Каковы свойства несмежных сторон четырехугольника?
Свойства несмежных сторон четырехугольника зависят от конкретной фигуры. Например, если несмежные стороны четырехугольника AB и CD перпендикулярны, то это может указывать на то, что фигура является прямоугольником.
Может ли одна сторона четырехугольника быть одновременно и смежной, и несмежной с другими сторонами?
Нет, одна сторона четырехугольника не может быть одновременно и смежной, и несмежной с другими сторонами. Смежные стороны имеют общую вершину, а несмежные стороны не имеют общей вершины.