Две вершины которые принадлежат одной стороне многоугольника называются

Ребра – суть основные элементы многоугольника, которые образуют его стороны. Каждое ребро соединяет две вершины и имеет определенную длину. Для определения ребер используются две вершины, а также порядок их расположения. Таким образом, ребра являются линиями, которые образуют границы многоугольника.

Вершины – это точки, в которых пересекаются ребра многоугольника. Вершинами могут быть любые точки на границе многоугольника. Вершины обладают особыми свойствами и являются ключевыми элементами для определения многоугольника. Каждая вершина имеет определенные координаты в пространстве и может быть одной из двух точек, находящихся на одной стороне многоугольника.

Таким образом, две вершины, которые принадлежат одной стороне многоугольника, называются ребрами. Ребра служат для определения формы и размера многоугольника, а также для создания его границ. Вершины же являются ключевыми точками, которые определяют углы и форму многоугольника. Знание этих терминов важно при работе с многоугольниками и изучении их свойств.

Содержание

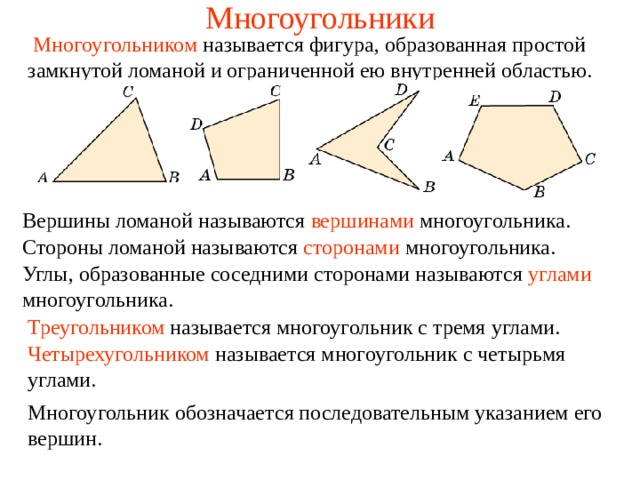
Что такое многоугольник

Каждая сторона многоугольника образует определенный угол с соседними сторонами, и сумма всех углов внутри многоугольника равна 360 градусам. Сторона, которая является отрезком между двумя вершинами, называется ребром многоугольника.

Многоугольники могут быть выпуклыми или невыпуклыми. Выпуклый многоугольник — это такой, у которого все углы вершин направлены внутрь фигуры. В невыпуклом многоугольнике углы вершин могут быть направлены как внутрь, так и наружу.

Каждая вершина многоугольника имеет соседние вершины, которые соединяются сторонами на одной и той же плоскости. Таким образом, две вершины, которые принадлежат одной стороне многоугольника, соседствуют друг с другом и образуют отрезок между ними.

Многоугольник — определение и особенности

Многоугольники можно классифицировать по числу сторон. Так, треугольник — самый простой многоугольник, имеющий три стороны и три угла. Четырехугольник, или квадрат, имеет четыре стороны и четыре прямых угла. Пятнадцатиугольник имеет пятнадцать сторон и пятнадцать углов.

Особенности многоугольников:

Внутренние углы: Сумма всех внутренних углов многоугольника равна (n-2) × 180 градусов, где n — число сторон многоугольника. Например, в треугольнике сумма углов равна 180 градусов, в пятиугольнике — 540 градусов.
Сумма длин сторон: Сумма длин всех сторон многоугольника называется периметром. Чтобы найти периметр многоугольника, нужно сложить длины всех его сторон.
Равносторонний многоугольник: Многоугольник, у которого все стороны равны друг другу, называется равносторонним.
Вписанный многоугольник: Многоугольник, у которого все вершины лежат на окружности, называется вписанным многоугольником.

Многоугольники являются важным понятием в геометрии и используются во многих областях, включая архитектуру, строительство и компьютерную графику.

Какие бывают многоугольники

Существует несколько разновидностей многоугольников:

Треугольник — многоугольник, состоящий из трех сторон и трех вершин. Отличается тем, что сумма внутренних углов равна 180 градусам.

Четырехугольник — многоугольник, состоящий из четырех сторон и четырех вершин. Может быть выпуклым или невыпуклым.

Пятиугольник, шестиугольник, семиугольник и так далее — многоугольники, состоящие из соответственно пяти, шести, семи и более сторон.

Выпуклый многоугольник — многоугольник, у которого все его углы внутренние и не превышают 180 градусов.

Невыпуклый многоугольник — многоугольник, у которого хотя бы один из его углов внешний и превышает 180 градусов.

Равносторонний многоугольник — многоугольник, у которого все его стороны равны.

Равнобедренный многоугольник — многоугольник, у которого хотя бы две его стороны равны.

Ромб — четырехугольник, у которого все его стороны равны. Отличается тем, что углы между его сторонами равны 90 градусам.

Знание различных типов многоугольников позволяет более глубоко изучать их свойства и применять их в различных математических задачах.

Стороны многоугольника

Каждая сторона многоугольника образуется двумя соседними вершинами. Две вершины, которые принадлежат одной стороне многоугольника, называются соседними вершинами.

Стороны многоугольника могут быть разной длины и ориентации. Ориентация стороны зависит от порядка в котором вершины соединены. Многоугольник может быть выпуклым или невыпуклым в зависимости от расположения его сторон.

Количество сторон многоугольника определяет его название. Например, треугольник имеет три стороны, четырехугольник — четыре, пятиугольник — пять и так далее.

Строение сторон многоугольника важно для изучения его свойств и характеристик. Знание о сторонах многоугольника помогает определить его периметр — сумму длин всех сторон, а также площадь — меру его поверхности.

Примеры свойств сторон многоугольника:

Равные стороны: если все стороны многоугольника имеют одинаковую длину, то многоугольник называется правильным;
Периметр: сумма длин всех сторон многоугольника;
Система координат: стороны многоугольника могут быть определены с помощью координат точек на плоскости.

Понимание сторон многоугольника является основополагающим для изучения геометрии и решения различных задач, связанных с этой геометрической формой.

Структура многоугольника: вершины, ребра и углы

Вершины многоугольника — это точки, в которых сходятся ребра многоугольника. Количество вершин в многоугольнике равно количеству его ребер. Вершины имеют координаты и могут быть обозначены буквами, например, A, B, C и т.д.

Ребра многоугольника — это отрезки, соединяющие две соседние вершины. Ребра задаются длиной, которая является единицей измерения отрезков. Ребра многоугольника также могут быть обозначены буквами, например, AB, BC, CD и т.д.

Углы многоугольника — это области пространства, образованные двумя смежными ребрами. Углы многоугольника обозначаются символом «∠» и могут быть измерены в градусах или радианах. Углы могут быть острыми, прямыми, тупыми или выпуклыми.

Структура многоугольника, состоящая из вершин, ребер и углов, позволяет определить его форму и свойства. Эта информация важна при решении геометрических задач и анализа многоугольников.

Связь вершин и ребер многоугольника

Каждое ребро многоугольника обладает двумя конечными точками — вершинами. Таким образом, можно сказать, что вершины и ребра многоугольника взаимосвязаны и составляют совокупность, определяющую границы фигуры.

Одна вершина многоугольника может быть соединена с несколькими ребрами, в то время как другая вершина может быть связана только с одним ребром. Это зависит от количества сторон, образующих многоугольник, и его формы.

Связь между вершинами и ребрами многоугольника определяет его внутреннюю структуру и форму. Математические и геометрические свойства этих связей позволяют исследовать и анализировать многоугольники, выявлять их особенности и характеристики.

Одна сторона многоугольника

Строение многоугольника зависит от его количества сторон. Если многоугольник имеет более трех сторон, он может быть выпуклым или невыпуклым. В случае выпуклого многоугольника все его стороны лежат по одну сторону от прямой, содержащей любую из его сторон, а углы внутри многоугольника не превышают 180 градусов. Когда многоугольник имеет внутренние углы более 180 градусов, он считается невыпуклым.

Характеристики одной стороны многоугольника:

Сторона многоугольника – это отрезок прямой, состоящий из двух точек, которые являются вершинами многоугольника.
Одна сторона многоугольника соединяет две соседние вершины многоугольника.
Строение и длина каждой стороны многоугольника могут быть разными.
Сумма длин всех сторон многоугольника равняется периметру многоугольника.

Таким образом, стороны многоугольника играют важную роль в его определении и свойствах. Они соединяют вершины многоугольника и определяют его форму и размеры.

Определение и свойства сторон многоугольника

Свойства сторон многоугольника:

1. Длина сторон	каждая сторона многоугольника имеет определенную длину, которая может быть измерена с использованием прямой или косвенными методами.
2. Количество сторон	многоугольник может иметь разное количество сторон. Например, треугольник имеет три стороны, четырехугольник — четыре, пятиугольник — пять и так далее.
3. Соотношения длин сторон	в некоторых многоугольниках длины сторон могут быть связаны определенными соотношениями, такими как равенство сторон в равностороннем треугольнике или пропорциональность сторон в подобных многоугольниках.
4. Углы сторон	каждая сторона многоугольника образует угол с соседними сторонами. Сумма всех углов многоугольника зависит от его количества сторон и может быть вычислена с помощью соответствующих формул.

Знание определения и свойств сторон многоугольника является важным при изучении геометрии и решении задач, связанных с расчетами и конструированием многоугольников.