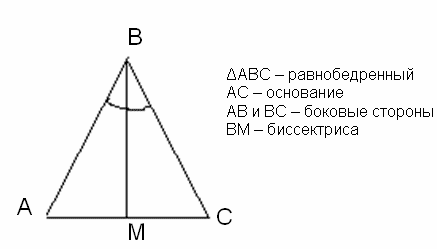
Треугольник – одна из основных фигур в геометрии, которая состоит из трех сторон и трех углов. Каждый треугольник описывается своими особыми свойствами, включая равнобедренность. Равнобедренный треугольник – это треугольник, у которого две стороны равны друг другу. Однако, чтобы понять, как назвать стороны равнобедренного треугольника, необходимо знать другие понятия в геометрии.
Существуют три основные стороны в треугольнике: основание и две боковые стороны. В случае равнобедренного треугольника, боковые стороны равны друг другу, а основание – третья сторона – отличается от боковых. Обычно, боковые стороны равнобедренного треугольника обозначаются буквами a и b, а основание – c.
Итак, в равнобедренном треугольнике мы имеем две одинаковые стороны, которые называются боковыми сторонами (a и b), и одну отличную от них сторону, которая называется основанием (c). Эти определения помогут нам лучше понять геометрические свойства равнобедренных треугольников и использовать их в решении различных задач и проблем.
Стороны треугольника равнобедренного
Равнобедренным называется треугольник, у которого две стороны равны. Такой треугольник имеет особые свойства и характеристики.
Основные понятия
В равнобедренном треугольнике:
- Боковые стороны — это равные стороны, которые соединяют вершины треугольника и лежат рядом с основой.
- Основа — это третья сторона, которая не является равной боковым сторонам.
- Вершины — это точки пересечения сторон треугольника.
Свойства равнобедренного треугольника
Стороны треугольника, являющегося равнобедренным, обладают следующими свойствами:
- Боковые стороны равны между собой. Таким образом, длина сторон AB и AC равна.
- Углы при основе равны. Это означает, что угол BAC равен углу BCA.
- Угол при вершине равен углу ABC.
Зная эти свойства, можно решать задачи, связанные с равнобедренными треугольниками, например, находить длины сторон или вычислять углы.
Равнобедренный треугольник: определение и свойства
Равнобедренный треугольник имеет несколько свойств:
1. Стороны
В равнобедренном треугольнике две стороны имеют одинаковую длину, а третья сторона называется основанием.
2. Углы
Углы при основании равнобедренного треугольника равны. Они обозначаются буквой «α». Другие два угла, называемые равными углами равнобедренного треугольника, обозначаются буквой «β».
Таким образом, у равнобедренного треугольника есть два равных угла α и один угол β, который является углом при основании.
Зная свойства равнобедренного треугольника, мы можем решать задачи на нахождение его периметра, площади, высот, а также нахождение неизвестных значений сторон и углов.
Пример:
Найдем площадь равнобедренного треугольника, если длина стороны равна 5 см, а высота, проведенная к основанию, равна 4 см.
Площадь равнобедренного треугольника можно найти по формуле: S = 0.5*a*h, где «a» — длина стороны, «h» — высота.
Подставим значения в формулу: S = 0.5 * 5 * 4 = 10 см²
Таким образом, площадь равнобедренного треугольника равна 10 см².
База равнобедренного треугольника
База равнобедренного треугольника – это одна из двух равных сторон, лежащая против угла, который не является вершиной двух равных сторон.
База равнобедренного треугольника не только определяет его форму, но и имеет некоторые свойства, которые могут быть полезными при решении задач на треугольники. Например, известно, что медиана, проведенная к базе равнобедренного треугольника, является биссектрисой и высотой данного треугольника.
Примеры:
Рассмотрим конкретный пример равнобедренного треугольника:
| Сторона | Значение |
|---|---|
| База (сторона AB) | 10 см |
| Равные стороны (сторона AC и сторона BC) | 12 см |
| Высота (AH) | 8 см |
| Медиана (AM) | 6 см |
Боковые стороны равнобедренного треугольника
В равнобедренном треугольнике наибольшая сторона называется основанием, а две равные стороны, которые образуют вершину треугольника, называются боковыми сторонами.
Боковые стороны равнобедренного треугольника также могут быть названы «равными сторонами», поскольку они имеют одинаковую длину.
Таким образом, боковые стороны равнобедренного треугольника играют важную роль в его конструкции и геометрических свойствах.
Равные стороны равнобедренного треугольника
Равнобедренным треугольником называется треугольник, у которого две стороны равны друг другу. Однако не все равные стороны в равнобедренном треугольнике имеют одно и то же название.
Главные равные стороны в равнобедренном треугольнике называются боковыми сторонами или равными сторонами. Они находятся против основания треугольника и имеют одинаковую длину.
Равные стороны в равнобедренном треугольнике также называются равновеликими сторонами, так как они образуют равные углы в основании треугольника.
Свойства равных сторон равнобедренного треугольника:
1. Боковые стороны равны друг другу: В равнобедренном треугольнике боковые стороны имеют одинаковую длину. Это означает, что каждая из этих сторон равна друг другу, то есть AB = AC.
2. Равные стороны образуют равные углы: Боковые стороны равнобедренного треугольника также образуют равные углы с основанием треугольника. Если сторона AB равна стороне AC, то угол BAC будет равным углу BCA.
Равнобедренный треугольник и его высота
Высота равнобедренного треугольника — это перпендикуляр, опущенный из вершины треугольника на основание (сторону, которая не равна другим двум).
Свойства высоты равнобедренного треугольника:
- Высота равнобедренного треугольника делит его основание на две равные части.
- Высота равнобедренного треугольника является медианой и биссектрисой одновременно.
- Высота равнобедренного треугольника является осью симметрии для всех его биссектрис и медиан.
Высота равнобедренного треугольника играет важную роль при решении задач связанных с его площадью, углами и теоремой Пифагора.
- Равнобедренный треугольник имеет две равные стороны.
- Высота равнобедренного треугольника является перпендикуляром, опущенным из вершины на основание треугольника.
- Высота делит основание на две равные части.
- Высота равнобедренного треугольника является медианой и биссектрисой одновременно.
- Высота равнобедренного треугольника является осью симметрии для всех его биссектрис и медиан.
Равнобедренный треугольник и его медианы
Медианами треугольника называются отрезки, соединяющие вершины треугольника с серединами противоположных сторон. В равнобедренном треугольнике медиана, проведенная из вершины, совпадает с биссектрисой угла при этой вершине. Таким образом, равнобедренный треугольник имеет три медианы, которые совпадают с высотами и биссектрисами углов треугольника.
Равнобедренный треугольник симметричен относительно медиан, что делает его особенно интересным для изучения. Например, сумма любых двух медиан равна третьей медиане, а также они делятся в отношении 2:1.
Важно отметить, что медианы равнобедренного треугольника пересекаются в одной точке, которая называется центром симметрии треугольника или точкой пересечения медиан. Эта точка делит каждую медиану в отношении 2:1.
Таким образом, равнобедренный треугольник и его медианы имеют целый ряд уникальных свойств, которые делают их предметом внимания в геометрии. Изучая эти свойства, можно получить глубокое понимание структуры и связей внутри равнобедренного треугольника.
Равнобедренный треугольник и его биссектрисы
Одной из важных характеристик равнобедренного треугольника являются его биссектрисы. Биссектриса в треугольнике — это отрезок, который делит угол треугольника на два равных угла. В равнобедренном треугольнике каждая из биссектрис делит противолежащую сторону на две равные части.
Биссектрисы равнобедренного треугольника

В равнобедренном треугольнике существует три биссектрисы:
| Биссектриса | Описание |
|---|---|
| Высота треугольника | Проведена из вершины треугольника к противолежащей стороне, перпендикулярно ей. |
| Медиана треугольника | Проведена из вершины треугольника к середине противолежащей стороны. |
| Вписанная окружность треугольника | Окружность, которая касается всех трех сторон треугольника. |
Свойства биссектрис равнобедренного треугольника
Биссектрисы равнобедренного треугольника обладают следующими свойствами:
- Высота треугольника делит противолежащую сторону на две равные части.
- Медиана треугольника делит противолежащую сторону на две равные части.
- Вписанная окружность треугольника имеет радиус, равный половине длины боковой стороны треугольника.
Изучение биссектрис равнобедренного треугольника поможет лучше понять его свойства и особенности, а также применять их в дальнейших геометрических вычислениях и конструкциях.
Свойства равнобедренного треугольника
1. Базы равнобедренного треугольника
Базы равнобедренного треугольника — это две равные стороны, которые образуют основание треугольника.
2. Углы равнобедренного треугольника
У равнобедренного треугольника два угла, прилежащие к основанию, равны друг другу. Эти углы называются основными углами.
Эти свойства равнобедренного треугольника позволяют нам решать задачи, связанные с вычислением его сторон и углов, а также использовать его в различных геометрических конструкциях.
Вопрос-ответ:
Что такое равнобедренный треугольник?
Равнобедренный треугольник — это треугольник, у которого две стороны равны по длине.
Какие стороны называются равнобедренного треугольника?
В равнобедренном треугольнике стороны, которые равны по длине, называются равными сторонами или боковыми сторонами.
Есть ли у равнобедренного треугольника специальные названия для сторон?
В равнобедренном треугольнике нет специальных названий для сторон.
Можно ли определить равнобедренность треугольника по его сторонам?
Да, можно определить равнобедренность треугольника, если две стороны равны по длине.
Как связаны между собой стороны и углы в равнобедренном треугольнике?
В равнобедренном треугольнике углы, противолежащие равным сторонам, равны по величине.
Как называется сторона треугольника, которая имеет равные длины с другой стороной?
Эта сторона называется равнобедренной стороной треугольника.
Есть ли какое-то специальное название для стороны треугольника, которая имеет разную длину с остальными сторонами?
Нет, все стороны треугольника, кроме равнобедренной, называются просто сторонами треугольника.