
Векторы — это одно из основных понятий в математике, физике и других естественных науках. Они представляют собой объекты, обладающие не только числовым значением, но и направлением. Векторы могут быть представлены геометрически стрелками, которые указывают направление и длину вектора.
Величины, которые могут быть охарактеризованы только числовым значением, не являются векторами. Например, длина отрезка, время, масса — все они не имеют направления и поэтому не являются векторами. Однако векторные величины могут быть связаны с этими не векторными величинами, например, ускорение можно представить векторно как вектор скорости.
Векторы играют важную роль в различных областях науки. В физике они используются для описания движения тел, сил, полей. В математике векторы используются для решения уравнений, геометрических построений, линейных отображений и многих других задач. Векторный анализ — это раздел математики, который изучает свойства векторов и их применение в различных областях знания.
Что такое числовая характеристика?
Числовая характеристика может быть представлена в виде числовой величины с плюсом или минусом, указывающим направление изменения. Например, если речь идет о скорости движения тела, положительное значение будет означать движение вперед, а отрицательное — движение назад.
Числовые характеристики могут быть как абсолютными, так и относительными. Абсолютные характеристики показывают точное значение измеряемой величины, например, массу тела или температуру. Относительные характеристики дают отношение одной величины к другой, например, процентное соотношение или коэффициенты.
Примеры числовых характеристик:
| Название | Описание |
|---|---|
| Скорость | Числовая характеристика, показывающая, как быстро движется объект |
| Температура | Числовая характеристика, отражающая степень нагретости или охлаждения среды |
| Вес | Числовая характеристика, указывающая на массу объекта |
| Уровень | Числовая характеристика, показывающая степень или меру чего-либо |
Числовые значения и их направление
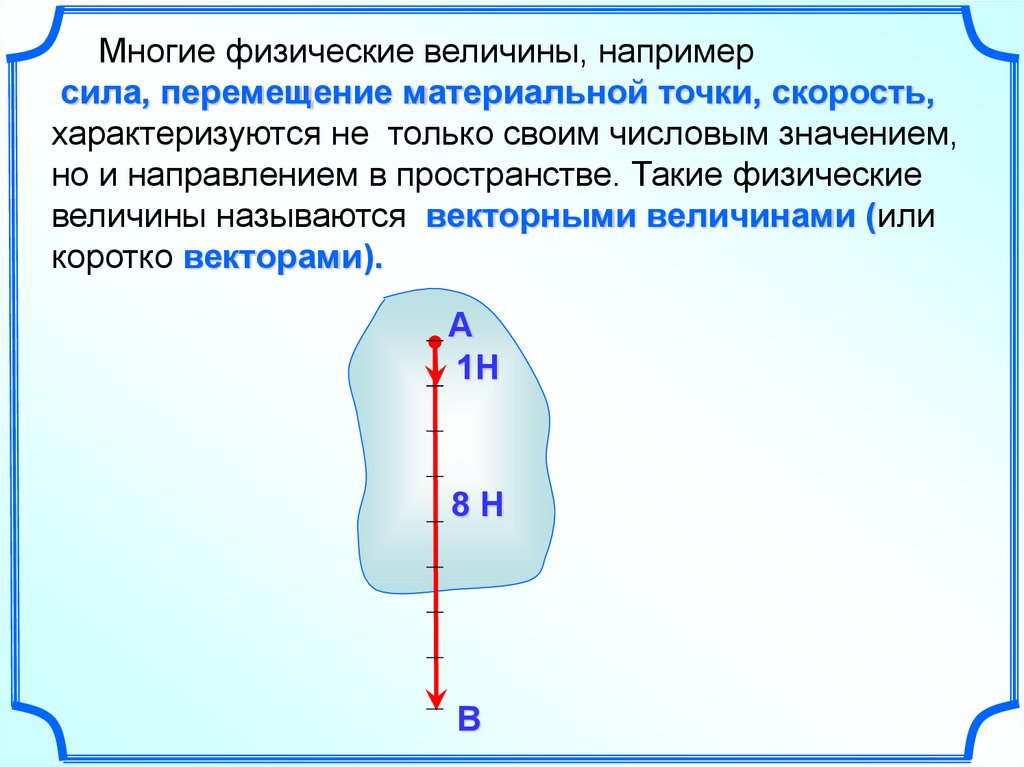
В математике и физике существуют величины, которые описываются не только числовым значением, но и направлением. Такие величины называются векторами.
Векторы широко применяются для описания физических явлений, движения тел и других процессов. Они позволяют ученным и инженерам более точно описывать их свойства и поведение.
Числовое значение вектора называется его модулем или абсолютной величиной, и оно всегда положительно. Модуль вектора показывает, насколько «длинным» является вектор. Направление вектора определяется углом относительно определенной оси или направления.
Вектор может быть направлен в одну из четырех сторон: вперед, назад, вверх или вниз. Понятие «направление» вектора очень важно при решении задач, так как оно может влиять на результаты вычислений.
Для удобства векторы часто представляют в виде стрелок, где длина стрелки соответствует модулю вектора, а ее направление указывает на направление вектора.
Основные операции с векторами включают сложение и вычитание. Сложение векторов выполняется по правилу «коммутативности», то есть порядок слагаемых не имеет значения. При вычитании векторов модули суммы и разности равны модулям исходных векторов, а направление определяется по правилу «обратное направление».
Таким образом, знание числовых значений и их направления позволяет более точно описывать и анализировать физические явления и процессы, а также решать различные задачи.
Определение числовых величин
Числовые величины могут быть представлены различными способами. Например, они могут быть представлены в виде арифметических чисел, десятичных дробей или в форме процентов. В зависимости от конкретной области применения, числовые величины могут быть выражены в разных единицах измерения.
Одна из основных характеристик числовых величин – их направление. Направление может быть положительным или отрицательным, в зависимости от того, каким образом величина изменяется. Например, положительное направление может указывать на рост числа, а отрицательное направление – на его уменьшение.
Числовые величины могут быть абсолютными или относительными. Абсолютные числовые величины представляют собой конкретные числовые значения, которые не зависят от других факторов. Относительные числовые величины, в свою очередь, зависят от других переменных и выражаются в процентах или коэффициентах.
Числовые величины играют важную роль в научных исследованиях, экономических анализах, моделировании и прогнозировании. Они позволяют описывать и измерять явления и процессы, а также понимать и предсказывать их изменения в будущем. Поэтому понимание и умение работать с числовыми величинами является необходимым навыком во многих областях деятельности.
Различные типы числовых характеристик
Числовые характеристики используются для описания и анализа различных величин, которые могут быть охарактеризованы числовым значением и направлением. При изучении данных и проведении статистического анализа важно учитывать разные типы числовых характеристик, которые позволяют описать разные аспекты и свойства исследуемых величин.
Абсолютные числовые характеристики
Абсолютные числовые характеристики представляют собой значения, которые выражаются в единицах измерения и являются конкретными числами. Такие характеристики могут быть использованы для измерения величин и определения их точного значения. Например, абсолютная числовая характеристика может быть представлена числом, указывающим на точную температуру или длину объекта.
Относительные числовые характеристики
Относительные числовые характеристики используются для описания величин в отношении других величин. Они позволяют проводить сравнение и анализ исследуемых значений относительно базового значения или других значений. Например, относительная числовая характеристика может быть представлена процентным соотношением или отношением двух численных значений.
Положительное и отрицательное направление
Величины охарактеризованные числовым значением могут иметь как положительное, так и отрицательное направление. Это связано с тем, что некоторые величины могут быть направлены в одну сторону (например, движение по прямой), в то время как другие величины могут быть направлены в противоположные стороны (например, сила тяжести и антитяжественность).
Положительное направление
Величины со значениями в положительном направлении имеют значения больше нуля и направлены вперед или вправо. Например, при движении по прямой оси координат положительное направление обозначается обычно стрелкой вправо или вперед.
Примеры положительных чисел:
- 3 (положительное число без ориентации)
- +5 (положительное число с явной указанной ориентацией)
- 10 (положительное число без ориентации)
Отрицательное направление
Величины со значениями в отрицательном направлении имеют значения меньше нуля и направлены назад или влево. Например, при движении по прямой оси координат отрицательное направление обозначается обычно стрелкой влево или назад.
Примеры отрицательных чисел:
- -2 (отрицательное число с явной указанной ориентацией)
- -7 (отрицательное число без ориентации)
- -12 (отрицательное число без ориентации)
Важно понимать, что положительное и отрицательное направление зависят от контекста и соглашений, поэтому необходимо учитывать эти факторы при работе с числовыми значениями.
Использование числовых характеристик в науке
Числовые характеристики играют важную роль в научном исследовании, позволяя ученым измерять и описывать явления и процессы с высокой точностью. Они помогают в создании математических моделей, находят применение в физике, химии, биологии, экономике и других научных областях.
Измерение и описание явлений
Числовые характеристики позволяют измерять физические, химические и биологические величины, такие как длина, масса, скорость, температура, концентрация и другие. Они помогают научным исследователям создавать точные и количественные описания явлений, а также проводить сравнительные анализы данных.
Математическое моделирование
Числовые характеристики также играют важную роль в математическом моделировании. Ученые используют математические модели для описания и предсказания различных явлений, применяя числовые характеристики в виде коэффициентов, параметров и переменных. Это позволяет анализировать сложные системы, прогнозировать результаты экспериментов и разрабатывать эффективные стратегии.
Примеры числовых характеристик
1. Среднее значение (математическое ожидание)
Среднее значение – это сумма всех значений, деленная на их количество. Оно показывает типичную характеристику объекта или явления и часто используется для измерения центральной тенденции данных.
2. Медиана
Медиана – это значение, которое делит упорядоченный набор данных на две равные части. Она позволяет определить «среднюю» характеристику данных без влияния выбросов.
3. Дисперсия и стандартное отклонение
Дисперсия и стандартное отклонение показывают разброс данных относительно их среднего значения. Дисперсия измеряется в квадратных единицах, а стандартное отклонение – в тех же единицах, что и исходные данные.
4. Коэффициент корреляции
Коэффициент корреляции показывает степень линейной связи между двумя или более переменными. Его значение лежит в диапазоне от -1 до 1, где -1 означает полную обратную зависимость, а 1 – полную прямую зависимость.
5. Доля или процент
Доля или процент – это отношение части к целому. Они позволяют оценить долю какой-либо характеристики в общей массе.
Это лишь небольшой перечень примеров числовых характеристик, которые используются в различных областях науки, экономики и статистики. Каждая из них имеет свою специфику применения и позволяет получить дополнительную информацию о исследуемых данных.
Методы измерения числовых величин
Величины, охарактеризованные числовым значением и направлением, называются векторными величинами. Измерение таких величин неразрывно связано с применением специальных методов и инструментов.
Прямые измерения
Одним из методов измерения векторных величин являются прямые измерения. Для этого используются приборы и инструменты, способные измерять величину и ее направление. Результаты прямых измерений могут быть представлены в виде чисел и записаны в соответствующих единицах измерения.
Измерение с использованием векторных диаграмм
Другим методом измерения числовых величин является использование векторных диаграмм. Векторные диаграммы позволяют наглядно представить величину и ее направление с помощью стрелок, длина и направление которых соответствуют измеряемым значениям. Такой метод измерения особенно полезен при работе с величинами, требующими представления в трехмерном пространстве.
| Метод измерения | Описание |
|---|---|
| Прямые измерения | Используются приборы для измерения величины и ее направления |
| Измерение с использованием векторных диаграмм | Векторные диаграммы помогают наглядно представить величину и ее направление |
Значение числовых характеристик для статистики
В статистике величины, охарактеризованные числовым значением и направлением, называются векторами. Они играют важную роль в анализе данных и позволяют проводить различные статистические исследования.
Векторы в статистике могут быть представлены в различных формах, например, в виде координат на плоскости или в пространстве. При этом их значения имеют особое значение для понимания статистических закономерностей и взаимосвязей в данных.
Среднее арифметическое является одним из наиболее распространенных показателей и представляет собой сумму всех значений вектора, разделенную на их количество. Оно позволяет определить типичное значение вектора и его положение относительно других величин.
Медиана представляет собой значение, которое находится в центре упорядоченного списка значений вектора. Она позволяет определить «среднюю» величину вектора, не зависимо от выбросов или аномальных значений.
Мода является самым часто встречающимся значением вектора. Она позволяет выявить наиболее типичные значения, которые встречаются чаще всего.
Дисперсия и стандартное отклонение указывают на степень разброса значений вектора относительно его среднего значения. Они позволяют определить уровень изменчивости и вариативности элементов вектора.
Вопрос-ответ:
Какие величины охарактеризованы числовым значением и направлением?
Величины, которые охарактеризованы числовым значением и направлением, называются векторами. Векторы используются для описания физических величин, таких как сила, скорость, ускорение и др.
Каким образом векторы охарактеризованы числовым значением и направлением?
Вектор описывается числовым значением, называемым модулем вектора, и направлением. Модуль вектора представляет собой длину вектора, а направление указывает на линию, вдоль которой располагается вектор.
Какие величины можно охарактеризовать числовым значением и направлением?
Величины, которые могут быть охарактеризованы числовым значением и направлением, включают в себя такие понятия, как сила, скорость, ускорение, момент и др. Эти величины могут быть представлены векторами, где числовое значение определяет их величину, а направление — например, направление движения, направление приложенной силы и т.д.
Что такое векторы и как они охарактеризованы?
Векторы — это величины, которые описываются числовым значением и направлением. Они используются для описания физических величин, таких как сила, скорость, ускорение и другие. Вектор охарактеризован значениями его модуля, который представляет собой длину вектора, и направлением, которое указывает на линию, вдоль которой направлен вектор.
