Параллельные отрезки – это одно из важных понятий в геометрии. Они имеют особое свойство, их граничные прямолинейные отрезки всегда не пересекаются, они никогда не встречаются.
Чтобы полностью понять понятие параллельности отрезков, необходимо знание того, что отрезки – это участки прямых линий, ограниченные двумя точками, называемыми концами отрезка. Два отрезка могут быть параллельными, только если они находятся в одной плоскости.
Основное свойство параллельных отрезков – это их характеристика не пересекаться при продолжении линий открытых концов. Если смотреть на них глазами, они будут лежать на разных прямых и никогда не касаться друг друга.
Что такое параллельные отрезки
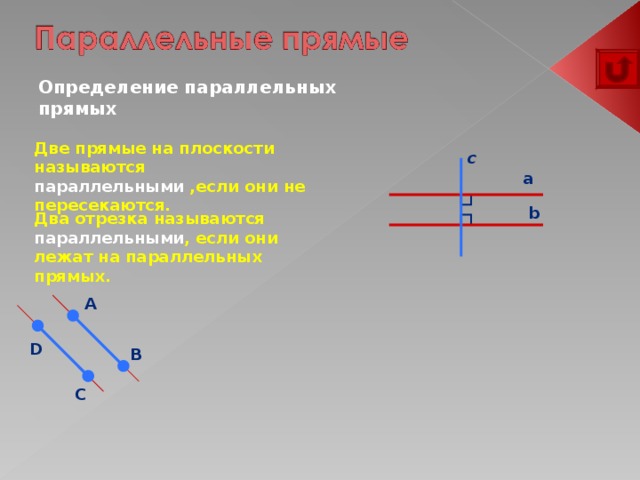
Параллельными отрезками называются два отрезка, которые лежат в одной плоскости и не пересекаются. Это означает, что у них нет общих точек, и они идут в одном направлении. Другими словами, если рассмотреть два параллельных отрезка, то можно провести прямую линию, которая будет пересекать только эти два отрезка и никакие другие. Такая прямая называется прямой параллельной данным отрезкам.
Параллельные отрезки имеют несколько свойств. Первое свойство заключается в том, что у них одинаковый наклон. Если рассмотреть параллельные отрезки на плоскости, то они будут идти в одном направлении и будут иметь одинаковую наклонную линию. Отрезки могут быть расположены как вертикально, так и горизонтально.
Второе свойство параллельных отрезков заключается в том, что расстояние между ними постоянно. Если измерить расстояние между двумя параллельными отрезками, то оно будет одинаковым на всем протяжении отрезков.
Параллельные отрезки встречаются в различных областях, где используется геометрия, таких как архитектура, инженерия, физика и т.д. Они играют важную роль при построении и расчете различных объектов и конструкций. Понимание свойств параллельных отрезков позволяет упростить анализ и управление этими объектами.
Определение параллельных отрезков
Для определения параллельности отрезков, часто используют термин «параллельность прямых». Две прямые называют параллельными, если они лежат на одной плоскости и не пересекаются ни в одной точке.
Для формального определения параллельности отрезков, можно использовать теорему о параллельных прямых, которая гласит: «Если две прямые пересекают одну прямую так, что сумма внутренних углов по одну сторону от пересекаемой прямой равна 180 градусов, эти прямые параллельны».
Свойства параллельных отрезков:
- Параллельные отрезки имеют одинаковый наклон и не пересекаются.
- Для параллельных отрезков выполняется теорема, согласно которой соответствующие углы, образованные параллельными прямыми и пересекаемой ими прямой, равны.
- Параллельные отрезки имеют равные длины.
Примеры параллельных отрезков:
| Отрезок AB | Отрезок CD |
|---|---|
| AB | CD |
| EF | GH |
| IJ | KL |
Условие параллельности отрезков
Два отрезка называются параллельными, если они лежат в одной плоскости и не имеют общих точек, то есть не пересекаются.
Условие параллельности отрезков можно сформулировать следующим образом:
1. Коэффициенты наклона
Два отрезка считаются параллельными, если их коэффициенты наклона равны.
Коэффициент наклона определяется отношением изменения y-координаты (вертикального сдвига) к изменению x-координаты (горизонтального сдвига) между двумя точками на отрезке.
Если два отрезка имеют одинаковый коэффициент наклона, то они параллельны.
2. Углы наклона
Два отрезка считаются параллельными, если их углы наклона равны.
Угол наклона отрезка определяется как угол между отрезком и горизонтальной осью, измеряемый против часовой стрелки.
Если у двух отрезков совпадают углы наклона, они параллельны.
Важно отметить, что эти условия относятся только к отрезкам, а не к прямым. Отрезки — это конечные участки прямых линий, имеющие начало и конец, в отличие от прямых, которые бесконечны в обоих направлениях.
Геометрические свойства параллельных отрезков
Основные геометрические свойства параллельных отрезков:
| Свойство | Описание |
|---|---|
| Равенство углов | Если две параллельные прямые пересекаются с третьей прямой, то соответствующие углы между пересекающимися прямыми равны. |
| Сумма углов | Для двух параллельных прямых и пересекающей их прямой сумма внутренних углов, образованных этими прямыми, равна 180 градусам. |
| Построение параллельного отрезка | Для построения параллельного отрезка к заданному отрезку, необходимо построить параллельные прямые, проведя концы заданного отрезка и используя компас или циркуль. |
Знание этих свойств позволяет более эффективно решать задачи, связанные с параллельными отрезками в геометрии.
Как найти параллельные отрезки
1. Проверьте, находятся ли отрезки на одной плоскости
Перед тем как определить параллельность отрезков, убедитесь, что они находятся на одной плоскости. Если отрезки лежат на разных плоскостях, они не могут быть параллельными.
2. Измерьте углы, образованные отрезками
Измерьте углы, образованные отрезками, используя транспортир или другой инструмент для измерения углов. Если углы, образованные отрезками, равны или сумма их равна 180 градусов, то отрезки являются параллельными.
3. Проверьте соотношение их углов
Проверьте соотношение углов между отрезками. Если углы между отрезками равны или их дополнения равны (сумма угла и его дополнения равна 180 градусов), то отрезки параллельны.
Важно помнить, что для определения параллельности отрезков необходимо иметь доступ к достаточному количеству информации, такой как углы и расстояния между отрезками. Используйте геометрические инструменты и формулы для более точного и надежного определения параллельности отрезков.
Примеры параллельных отрезков
Два отрезка называются параллельными, если они лежат на одной плоскости и не пересекаются ни в одной точке. Примеры параллельных отрезков могут быть найдены в различных областях, включая математику, геометрию и инженерное дело.
В геометрии, примером параллельных отрезков может быть два отрезка, расположенных на одной прямой и имеющих одинаковые углы наклона. Такие отрезки называются «горизонтальными» или «вертикальными» параллельными отрезками. Например, отрезки AB и CD на рисунке ниже являются параллельными, так как они лежат на одной горизонтальной прямой и имеют одинаковую высоту.
| A | B |
| C | D |
В инженерном деле, примером параллельных отрезков может быть два рельса, по которым движется поезд. Рельсы параллельны друг другу, так как они имеют постоянное расстояние между собой на протяжении всего пути.
В математике, параллельные отрезки также часто используются для построения прямоугольников, квадратов и параллелограммов. Например, стороны AB и CD на рисунке ниже являются параллельными отрезками, так как они лежат на одной плоскости и не пересекаются.
| A | B |
| C | D |
Примеры параллельных отрезков встречаются в различных ситуациях и областях, применение и понимание концепции параллельности отрезков является важным элементом в математике и геометрии.
Значимость параллельности отрезков для различных областей
В геометрии параллельные отрезки — это отрезки, которые лежат на параллельных прямых и имеют одинаковую направленность. Это основное определение, которое используется при решении геометрических задач. Параллельные отрезки позволяют строить и анализировать фигуры, вычислять площади и периметры, находить точки пересечения прямых и многое другое. Геометрия не обойдется без понимания параллельности отрезков.
В инженерии и архитектуре понятие параллельных отрезков также имеет большое значение. При проектировании зданий и сооружений необходимо учитывать множество аспектов, включая планировку помещений, расположение стен и перегородок. Здесь точность в измерениях и определении параллельности отрезков играет важную роль, так как от этого зависит прочность и эстетичность конструкции.
| Область | Значимость параллельности отрезков |
|---|---|
| Геометрия | Основное понятие для построения фигур и вычислений |
| Инженерия и архитектура | Влияет на точность и эстетичность конструкций |
| Математическая статистика | Используется при интервальной оценке параметров |
Однако, параллельность отрезков важна не только в вышеперечисленных областях. Ее значимость распространяется и на другие сферы, такие как компьютерное моделирование, криптография, линейное программирование и даже в искусстве, где параллельные элементы создают гармоничные и сбалансированные композиции.
Таким образом, знание и понимание понятия параллельности отрезков имеет большое значение в различных областях знаний и помогает решать сложные задачи, анализировать данные, строить качественные конструкции и создавать искусство.
Вопрос-ответ:
Как определить, что два отрезка параллельны?
Два отрезка считаются параллельными, если они не имеют общих точек и расположены на одной плоскости так, что их угол наклона одинаковый.
Если два отрезка имеют одинаковый угол наклона, это означает, что они параллельны?
Нет, одинаковый угол наклона отрезков не означает, что они параллельны. Для того чтобы утверждать о параллельности отрезков, необходимо, чтобы они были на одной плоскости и не имели общих точек.
Может ли один отрезок быть параллельным самому себе?
Нет, отрезок не может быть параллельным самому себе, так как параллельность определяется отношением между двумя отрезками, а не отрезком самим по себе.
Обязательно ли, чтобы отрезки находились на одной плоскости, чтобы быть параллельными?
Да, для того чтобы можно было говорить о параллельности двух отрезков, они должны быть на одной плоскости. Если отрезки находятся в пространстве и не лежат в одной плоскости, то говорят, что они скрещиваются.
Как можно проверить, что два отрезка параллельны с помощью уравнений?
Для проверки параллельности отрезков с помощью уравнений, нужно записать уравнения прямых, на которых лежат отрезки, и сравнить их угловые коэффициенты. Если угловые коэффициенты равны, то отрезки параллельны.