
Понятие параллельности прямых – одно из основных в евклидовой геометрии. Две прямые называются параллельными, если они лежат в одной плоскости и не пересекаются, то есть не имеют общих точек. Параллельность является одной из фундаментальных идей в геометрии и лежит в основе понятия параллельных линий, плоскостей и пространств.
Параллельные прямые идеально подходят для описания направления движения, углов обзора и расположения объектов в пространстве. Они находят широкое применение в различных областях науки и техники, включая математику, физику, геодезию и информатику.
В геометрии параллельность прямых связана с концепцией параллельных линий, где две прямые считаются параллельными, если они никогда не пересекаются, даже при продолжении в бесконечности. Это ключевое понятие в геометрии, которое помогает в описании и анализе трехмерных объектов и явлений.
Определение параллельности прямых в трехмерном пространстве
Две прямые в трехмерном пространстве считаются параллельными, если они не пересекаются и не лежат на одной плоскости.
В трехмерной геометрии прямые могут иметь различное положение относительно друг друга. Если две прямые не имеют точек пересечения и не могут быть приведены в одну плоскость, то они считаются параллельными.
Чтобы определить параллельность прямых, нужно проверить условия их непересечения и отсутствия общей плоскости:
- Непересечение: Если прямые имеют общую точку или пересекаются в какой-то другой точке, то они не являются параллельными.
- Отсутствие общей плоскости: Если прямые лежат на одной плоскости, то они не считаются параллельными. Если же они не могут быть приведены в одну плоскость, то они параллельны.
Таким образом, параллельность прямых можно определить, основываясь на их пересечении и положении в пространстве. Это важное понятие в геометрии, которое используется в различных областях, таких как физика, инженерия и архитектура.
Обратите внимание, что параллельность прямых может быть проверена с помощью геометрических методов, а также аналитической геометрии, используя уравнения прямых.
Понятие параллельности прямых
Если две прямые имеют общую точку, они называются скрещивающимися, или пересекающимися. Если две прямые лежат в разных плоскостях и не пересекаются, то они называются скрещивающимися в пространстве.
Свойства параллельных прямых:
- Они лежат в одной плоскости;
- Они имеют одинаковое направление;
- Расстояние между ними постоянно и не меняется ни при каких условиях;
- Они никогда не пересекаются.
Примеры параллельных прямых:
| Прямая 1 | Прямая 2 |
|---|---|
| a: x + 2y = 5 | b: 2x + 4y = 10 |
| a: x — y = 3 | b: 2x — 2y = 6 |
| a: 3x + 2y — z = 0 | b: 6x + 4y — 2z = 0 |
Условия параллельности прямых
Две прямые в пространстве называются параллельными, если выполняются следующие условия:
-
Условие 1:
Две прямые имеют одинаковые направляющие векторы.
-
Условие 2:
Две прямые не пересекаются, то есть не имеют общих точек.
Если выполнены оба условия, то можно сказать, что прямые параллельны. В противном случае, они называются скрещивающимися.
Для определения параллельности прямых можно использовать различные методы. Один из самых простых способов — проверка равенства направляющих векторов. Если две прямые имеют одинаковые векторы, то они параллельны. Другой способ — проверка отсутствия общих точек у прямых, что означает их различие в пространстве и, следовательно, параллельность.
| Условие | Параллельность | Скрещивающиеся прямые |
|---|---|---|
| Условие 1 | Выполнено | Не выполнено |
| Условие 2 | Выполнено | Не выполнено |
Если параллельные прямые находятся на одной плоскости, то они называются плоскостными параллельными прямыми. В этом случае они все еще имеют одинаковые направляющие векторы, но также лежат на одной плоскости.
Знание и понимание условий параллельности прямых важно в геометрии и может использоваться для решения задач и построения отрезков, прямоугольников, кубов и других фигур.
Случай параллельности двух прямых
Признаки параллельности прямых:
1. Значение углов между прямыми: В случае параллельности двух прямых, углы между ними будут равными 0 градусов. Это значит, что прямые лежат на одной линии и не сходятся ни в одной точке. Если угол между прямыми не равен 0 градусов, то они не являются параллельными.
2. Значение коэффициента наклона прямых: Две прямые в плоскости параллельны, если их угловые коэффициенты k1 и k2 равны между собой. Угловой коэффициент прямой определяет, как быстро прямая меняет свое положение по оси x при изменении положения по оси y. Если значения угловых коэффициентов прямых отличаются, то они не являются параллельными.
Пример:
Рассмотрим две прямые в плоскости, заданные уравнениями:
l1: y = 2x + 3
l2: y = 2x + 6
Обе прямые имеют одинаковые угловые коэффициенты 2, следовательно, они параллельны. При этом прямые имеют разные точки пересечения с осью y (точки (0, 3) и (0, 6)), что объясняет различие в их положении относительно друг друга.
Параллельные плоскости и прямые
Математическое понятие параллельности касается не только прямых, но и плоскостей. Плоскости считаются параллельными, если они не имеют общих точек или имеют только общие прямые.
Если две плоскости параллельны, то любая прямая, принадлежащая одной из них, будет параллельна другой плоскости. Также все прямые, параллельные плоскости, будут параллельны между собой.
Как и в случае с прямыми, параллельные плоскости обладают рядом свойств:
1. Взаимное расположение плоскостей
Параллельные плоскости не пересекаются и не сходятся в бесконечности. Они расположены параллельно друг другу и имеют одинаковые углы наклона.
2. Отношение расстояний
Расстояние между параллельными плоскостями является постоянным и не зависит от положения плоскости в пространстве.
Таким образом, понимание параллельности плоскостей и прямых является важным в математике и находит применение в различных областях, включая геометрию, физику и инженерные науки.
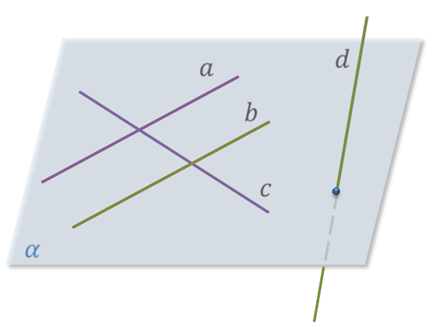
Параллельные прямые в разных плоскостях
В геометрии две прямые называются параллельными, если они лежат в одной плоскости и не пересекаются. Однако, в некоторых случаях прямые могут быть параллельными, даже если они лежат в разных плоскостях.
Представим себе две плоскости, обозначим их как П1 и П2. Допустим, что на плоскости П1 есть прямая L1, и на плоскости П2 есть прямая L2. Если L1 и L2 не пересекаются, то они называются параллельными прямыми в разных плоскостях.
Параллельные прямые в разных плоскостях имеют некоторые интересные свойства. Например, если мы проведем плоскость, параллельную П1 и П2, то эта плоскость будет пересекать L1 и L2 под прямыми углами. Это связано с особенностями разных плоскостей и прямых, лежащих в них.
Иногда параллельные прямые в разных плоскостях встречаются в различных сферах, таких как архитектура и инженерное дело. Знание и понимание свойств параллельных прямых в разных плоскостях помогает строителям и проектировщикам создавать прочные и надежные конструкции.
Таким образом, параллельные прямые в разных плоскостях являются важным понятием в геометрии и находят применение в различных сферах человеческой деятельности.
Необходимость и достаточность условий параллельности
Для того чтобы две прямые в пространстве можно было назвать параллельными, необходимо и достаточно выполнение определенных условий.
Необходимым и, в то же время, достаточным условием параллельности двух прямых является существование третьей прямой, которая перпендикулярна обеим заданным прямым.
Если две прямые имеют общую перпендикулярную, то они называются параллельными.
Это условие является необходимым, так как две параллельные прямые не могут пересекаться. Условие также является достаточным, так как присутствие перпендикулярной прямой гарантирует, что две заданные прямые не пересекаются.
Таким образом, чтобы убедиться в параллельности двух прямых, необходимо найти их общую перпендикулярную. Если такая прямая существует, то две заданные прямые можно считать параллельными.
Параллельные прямые и третья, пересекающая их прямая
Однако возникает вопрос, что происходит, когда к этим параллельным прямым добавляется третья прямая, непараллельная первым двум?
Третья прямая, пересекающая параллельные прямые, может возрастать вдоль одной из параллельных прямых и уменьшаться по направлению другой параллельной прямой. Таким образом, на отрезке, где параллельные прямые пересекаются, третья прямая будет иметь определенный наклон в отношении параллельных прямых.
Исследование взаимодействия трех прямых может охватывать такие понятия, как углы, трехмерные геометрические фигуры и другие.
Понимание особенностей параллельных прямых и третьей, пересекающей их прямой, позволяет более глубоко изучить пространственные отношения и взаимосвязи между геометрическими объектами.
Практическое применение параллельных прямых
Параллельные прямые имеют широкое применение в различных областях науки и техники. Они играют важную роль в геометрии, строительстве, машиностроении, компьютерной графике и других областях.
Геометрия
В геометрии параллельные прямые используются для построения и анализа различных фигур и фигурных систем. Например, параллельные прямые позволяют определить их свойства и классифицировать фигуры. Они также используются в задачах на плоскости и в пространстве, связанных с прямыми и плоскостями.
Строительство
В строительстве знание параллельных прямых позволяет строить прямые сооружения. Например, при постройке дорог параллельные прямые используются для выравнивания и нивелирования дорожного полотна, что обеспечивает его гладкость и комфортность движения.
Также параллельные прямые используются при сооружении зданий и сооружений, для размещения трубопроводов, кабелей и других инженерных коммуникаций.
Машиностроение
В машиностроении знание параллельных прямых используется для точного изготовления и сборки деталей и узлов. Параллельные прямые применяются, например, в процессе обработки металлических изделий на станках и в проектировании инструментов и приспособлений.
Точное параллельное расположение прямых является важным условием для достижения высокой точности и качества изделий.
Компьютерная графика
В компьютерной графике параллельные прямые используются для построения трехмерных объектов и их визуализации. Они позволяют создавать реалистичные и пространственные изображения виртуальных миров.
Программы компьютерной графики используют математические алгоритмы для создания и отображения параллельных прямых на экране, что позволяет создавать сложные трехмерные сцены и анимации.
| Область применения | Примеры |
|---|---|
| Геометрия | Классификация фигур, решение задач на плоскости и в пространстве |
| Строительство | Выравнивание дорожного полотна, размещение инженерных коммуникаций |
| Машиностроение | Обработка металлических изделий, сборка деталей и узлов |
| Компьютерная графика | Построение трехмерных объектов, визуализация виртуальных миров |
Вопрос-ответ:
Что обозначает понятие «параллельные прямые» в пространстве?
Параллельные прямые в пространстве — это две прямые линии, которые лежат в одной плоскости и не пересекаются ни в одной точке.
Как можно доказать, что две прямые в пространстве параллельны?
Существует несколько способов доказательства параллельности двух прямых в пространстве. Например, можно использовать теорему о параллельных линиях, которая гласит, что если две прямые пересекаются третьей прямой так, что сумма внутренних углов на одной стороне равна 180 градусов, то эти две прямые параллельны.
Какие свойства имеют параллельные прямые в пространстве?
Параллельные прямые в пространстве обладают рядом свойств. Например, они имеют одинаковые наклоны и не пересекаются ни в одной точке. Также прямая, проведенная через любую точку одной из параллельных прямых и параллельная другой прямой, будет пересекать ее в одной и только одной точке.
Что происходит, если две прямые в пространстве не параллельны?
Если две прямые в пространстве не параллельны, то они пересекаются в одной и только одной точке. Такая точка называется точкой пересечения. При этом, если две прямые пересекаются в одной точке, то они не могут быть параллельными.